洛谷——P1227 [JSOI2008]完美的对称

P1227 [JSOI2008]完美的对称

题目描述

在峰会期间，必须使用许多保镖保卫参加会议的各国代表。代表们除了由他自己的随身保镖保护外，组委会还指派了一些其他的特工和阻击手保护他们。为了使他们的工作卓有成效，使被保卫的人的安全尽可能得到保障，保镖被分配到被保护人的各个方向。

保镖的最佳站立位置应该是这样的：被保护人应站在所有保镖的对称中心。但是，只要被保

护人一移动，保镖就很难根据要人的新位置调整位置。大多数的特工都很难对此作出实时调整。

因此，安全部长决定将该过程逆转一下，保镖先站好自己的位置，然后要人在他们的对称中心找到合适的位置。如果要人随便走动，我们就对他的安全不必负责。

你的工作是使这个过程自动操作。给出一组N个点（保镖的位置），你要找出它们的对称中心S，在这儿被保护人将相对安全。下面以此类推。

首先我们给定一点A以及对称中心S，点A'是点A以S为对称中心形成的像点，即点S是线段AA'的对称中心。

点阵组（X）以S为中心的像点是由每个点的像点组成的点阵组。X是用来产生对称中心S的，即点阵X以S为中心的像点的集合即为点阵X本身。

输入输出格式

输入格式：

输入文件第一行是一个整数N，1<=N<=20000，接下来的N行每行包含用空格隔开的两个整数Xi和Yi，-100000<=Xi,Yi<=100000，表示这组点阵中第I个点的笛卡尔坐标值。

因为任何两个保镖都不会站在同一个位置上，所以在给定的作业中，任何两点都不相同。但注意保镖可以站在被保护人相同的位置。

输出格式：

输出文件仅有一行。如果给定的点阵能产生一个对称中心，则输出“V.I.P. should stay at (x,y).”，其中X和Y代表中心的笛卡尔坐标值，格式为四舍五入保留至小数点后一位。

如果该组点阵无对称中心，输出"This is a dangerous situation!"，注意输出时除了两个单词之间用一个空格隔开外，不要输出多余空格。

输入输出样例

输入样例#1：

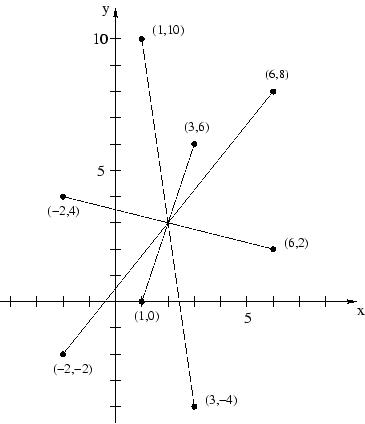
8
1 10
3 6
6 8
6 2
3 -4
1 0
-2 -2
-2 4

输出样例#1：

V.I.P. should stay at (2.0,3.0).

说明

[JSOI2008]第二轮

宝宝不明白这个题为什么会是省选的题、、

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 20001
using namespace std;
double xx,yy;
int n,sx,sy,x[N],y[N];
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
int main()
{
    n=read();
    ;i<=n;i++)
     x[i]=read(),y[i]=read(),sx+=x[i],sy+=y[i];
    xx=1.0*sx/n,yy=1.0*sy/n;
    printf("V.I.P. should stay at (%.1lf,%.1lf).",xx,yy);
    ;
}

64分代码（没有考虑没有对称中心的情况，其实我认为应该是都有对称中心的）

我们知道对称中心一定是一组对称数的中间位置，如果这些数有对称中心的话，所有的对称点到对称中心的位置是相同的，对称中心的位置即为这两个数x的中间，y为这两个数y的中间，我们可以直接将这些直接加起来然后在除以数的个数，这算出来的应该是对称中心，然后我们在判断这些点的对称中心在不在这个地方

一对对称点一定是如果一个点的x小，那么另一个的x一定大，这样我们排一下序，看一下是对称点的两个数的对称点是否在这个位置

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 20001
using namespace std;
double xx,yy;
int n,sx,sy;
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
struct A
{
    int x,y;
}a[N];
int cmp(A a,A b)
{
    if(a.x!=b.x) return a.x<b.x;
    if(a.y!=b.y) return a.y<b.y;
}
int main()
{
    n=read();
    ;i<=n;i++)
     a[i].x=read(),a[i].y=read(),sx+=a[i].x,sy+=a[i].y;
    xx=1.0*sx/n,yy=1.0*sy/n;
    sort(a+,a++n,cmp);
    ;i<=n;i++)
     ].x)/!=xx||].y)/!=yy)
      {
          printf("This is a dangerous situation!");
          ;
      }
    printf("V.I.P. should stay at (%.1lf,%.1lf).",xx,yy);
    ;
}

AC代码