LeetCode之Weekly Contest 91
第一题:柠檬水找零
问题:
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。
顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
示例 1:
输入:[5,5,5,10,20]
输出:true
解释:
前 3 位顾客那里,我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里,我们收取一张 10 美元的钞票,并返还 5 美元。
第 5 位顾客那里,我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零,所以我们输出 true。
示例 2:
输入:[5,5,10]
输出:true
示例 3:
输入:[10,10]
输出:false
示例 4:
输入:[5,5,10,10,20]
输出:false
解释:
前 2 位顾客那里,我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客,我们收取一张 10 美元的钞票,然后返还 5 美元。
对于最后一位顾客,我们无法退回 15 美元,因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零,所以答案是 false。
提示:
0 <= bills.length <= 10000bills[i]不是5就是10或是20
链接:https://leetcode-cn.com/contest/weekly-contest-91/problems/lemonade-change/
分析:
1.如果是5,不需要找回
2.如果是10,必须有至少一个5
3.如果是20,必须有至少三个5或者1个10和1个5
通过变量分别记录5/10/20个数,然后通过收支进行调整即可,一旦不满足上面3个条件即fail
AC Code:
1 class Solution {
2 public:
3 bool lemonadeChange(vector<int>& bills) {
4 //分别记录当前有的钱,贪心找回,如果能找钱则pass
5 int m5=0;
6 int m10 = 0;
7 int m20 = 0;
8 for (int i = 0; i < bills.size(); i++)
9 {
10 if (bills[i] == 5)
11 {
12 m5 += 1;
13 continue;
14 }
15 if (bills[i] == 10)
16 {
17 if (m5 >= 1)
18 {
19 m10++;
20 m5--;
21 continue;
22 }
23 else
24 {
25 return false;
26 }
27 }
28 if (bills[i] == 20)
29 {
30 if (m10 >= 1 && m5>=1) //有一个10块钱的和1个五块的
31 {
32 //10+5
33 m10--;
34 m5--;
35 m20++;
36 continue;
37 }
38 if (m5 >= 3) //3个五块的
39 {
40 m5 -= 3;
41 m20++;
42 continue;
43 }
44 return false;
45 }
46 }
47 return true;
48 }
49 };
其他:
用时最少(8ms/24ms)做法:
static int x=[](){
std::ios::sync_with_stdio(false);
cin.tie(NULL);
return 0;
}();
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int n1 = 0;
int n2 = 0;
for (int i = 0; i < bills.size(); i++){
if (bills[i] == 5){
n1++;
}else if (bills[i] == 10){
if (n1 <= 0)
return false;
else
n1--, n2++;
}else{
if (n1 >= 1 && n2 >= 1)
n1--,n2--;
else if (n1 >= 3)
n1 -= 3;
else
return false;
}
}
return true;
}
};
1.20的个数没必存储。
2.学习高手code时候经常看到
static int x=[](){
std::ios::sync_with_stdio(false);
cin.tie(NULL);
return 0;
}();
参考https://www.cnblogs.com/PrayG/p/5749832.html
“
百 度了一下,原来而cin,cout之所以效率低,是因为先把要输出的东西存入缓冲区,再输出,导致效率降低,而这段语句可以来打消iostream的输入 输出缓存,可以节省许多时间,使效率与scanf与printf相差无几
sync_with_stdio
这个函数是一个“是否兼容stdio”的开关,C++为了兼容C,保证程序在使用了std::printf和std::cout的时候不发生混乱,将输出流绑到了一起。
在默认的情况下cin绑定的是cout,每次执行 << 操作符的时候都要调用flush,这样会增加IO负担。可以通过tie(0)(0表示NULL)来解除cin与cout的绑定,进一步加快执行效率。
”
以后应该也养成这个习惯,至少在OJ场景下这样使用。此外还有看到#include<bits/stdc++.h>,据说是直接包含了C++所包含的所有头文件,不过用的VS2013 社区版,并不能直接这样用。
第二题:二叉树中所有距离为K的结点
题目:
给定一个二叉树(具有根结点 root), 一个目标结点 target ,和一个整数值 K 。
返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。
示例 1:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2 输出:[7,4,1] 解释:
所求结点为与目标结点(值为 5)距离为 2 的结点,
值分别为 7,4,以及 1
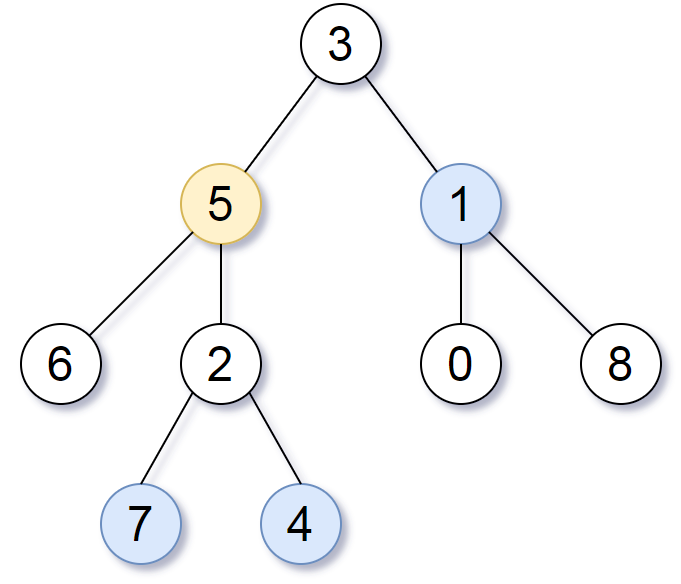
注意,输入的 "root" 和 "target" 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。
提示:
- 给定的树是非空的,且最多有
K个结点。 - 树上的每个结点都具有唯一的值
0 <= node.val <= 500。 - 目标结点
target是树上的结点。 0 <= K <= 1000.
链接:https://leetcode-cn.com/contest/weekly-contest-91/problems/all-nodes-distance-k-in-binary-tree/
分析:
对二叉树掌握不够扎实,本来想要重新构建,得到一个能够上溯双亲节点的双向链表,最终失败了,后来琢磨重新编码,其实就是利用满二叉树的性质。
1.对数据进行编码映射,编码规则为根节点为1,左子节点编码为父节点编码*2,右子节点编码为父节点编码*2+1,即得到满二叉树时候对应的位置
2.这样满足如下性质:如果最低位是0,则为左侧节点,否则是右侧节点,任一编码/2的结果即为其父节点编码
3.找后代节点只需要递归查找即可
4.如果上面某个距离正好满足要求,则说明某一祖先即为待求节点,否则找同在该祖先下的堂亲节点,利用编码得到的左右,找到另一侧的后代节点即可。
AC code:
1 /**
2 * Definition for a binary tree node.
3 * struct TreeNode {
4 * int val;
5 * TreeNode *left;
6 * TreeNode *right;
7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {}
8 * };
9 */
10 class Solution {
11 public:
12 vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
13 vector<int> ret; //存储结果
14 map<uint64_t, TreeNode> data; //存储重新编码后的数据,key:编码,value:节点
15 data = DealTreeNode(root, 1);
16 //完成对数据的转换,接下来找到目标位置
17 int targetcode;
18 for (map<uint64_t, TreeNode>::iterator it = data.begin(); it != data.end(); it++)
19 {
20 if (target->val == (*it).second.val)
21 {
22 targetcode = (*it).first; //根据target的值找到该值对应的编码
23 break;
24 }
25 }
26
27 //向下找K层,向上一层的另一侧向下找K-1-1层,向上i(i<K)层的另一侧向下找K-i-1层,向上找K层的一个
28 vector<int> tmp; //存储每一次查找的结果
29 TreeNode tmpnode(0);
30 uint64_t tmpcode = targetcode;
31 map<uint64_t, TreeNode>::iterator tmpit;
32 for (int i = 0; i <= K; i++)
33 {
34 if (i == 0) //只有起始target才直接找后代节点
35 {
36 //向下找
37 //i=0,即target节点位置
38 //向下直接找K层,即为后代中距离为K的节点
39 tmp = GetDownKDistance(target, K);
40 ret = addVector(ret, tmp);
41 continue;
42 }
43 if (tmpcode <=1) //编码位置起始 1,达到根节点没办法继续向上追溯
44 {
45 break;
46 }
47 if (i == K)
48 {
49 //可能某一个祖先节点正好是距离K
50 tmpit = data.find(tmpcode / 2);
51 ret.push_back((*tmpit).second.val);
52 break; //达到这一的祖先节点,则结束
53 }
54 //找表亲节点
55 //根据最后一位确定表亲位置
56 if (tmpcode & 1 == 1)
57 {
58 //当前节点是右节点
59 tmpit = data.find(tmpcode - 1);
60 if (tmpit != data.end())
61 {
62 //说明存在这样一个表亲节点
63 tmp = GetDownKDistance(&((*tmpit).second), K -i-1);
64 ret = addVector(ret, tmp);
65 }
66 }
67 else
68 {
69 //当前节点是左节点
70 tmpit = data.find(tmpcode + 1);
71 if (tmpit != data.end())
72 {
73 tmp = GetDownKDistance(&((*tmpit).second), K - i-1);
74 ret = addVector(ret, tmp);
75 }
76 }
77 tmpcode /= 2; //处理上一层
78 }
79 return ret;
80 }
81 vector<int> addVector(vector<int> v1, vector<int> v2)
82 {
83 vector<int> ret;
84 for (int i = 0; i < v1.size(); i++)
85 {
86 ret.push_back(v1[i]);
87 }
88 for (int i = 0; i < v2.size(); i++)
89 {
90 ret.push_back(v2[i]);
91 }
92 return ret;
93 }
94 //递归查找后代节点
95 vector<int> GetDownKDistance(TreeNode* root, int K)
96 {
97 vector<int> ret;
98 vector<int> left,right;
99 if (root == nullptr) //如果节点为空,则不会有距离K的后代
100 {
101 return ret;
102 }
103 if (K == 0) //K==0,则为目标,返回对应的值
104 {
105 ret.push_back(root->val);
106 return ret;
107 }
108 //当前K层,则后代K-1层,递归查找
109 left = GetDownKDistance(root->left, K - 1);
110 right = GetDownKDistance(root->right, K - 1);
111 ret=addVector(ret,left);
112 ret=addVector(ret,right);
113 return ret;
114 }
115 //用于递归生成新的数据结构
116 map<uint64_t, TreeNode> DealTreeNode(TreeNode* root,int level)
117 {
118 map<uint64_t, TreeNode> ret;
119 map<uint64_t, TreeNode> left, right;
120 TreeNode tmp(0);
121 if (root == nullptr)
122 {
123 return ret;
124 }
125 tmp.val = root->val;
126 tmp.left = root->left;
127 tmp.right = root->right;
128 ret.insert(make_pair(level, tmp));
129 left = DealTreeNode(root->left, level * 2);
130 right = DealTreeNode(root->right, level * 2 + 1);
131 for (map<uint64_t, TreeNode>::iterator it = left.begin(); it!=left.end(); it++)
132 {
133 ret.insert(*it);
134 }
135 for (map<uint64_t, TreeNode>::iterator it = right.begin(); it != right.end(); it++)
136 {
137 ret.insert(*it);
138 }
139 return ret;
140 }
141
142 };
其他:
用时最少的做法(4/12ms):
1 /**
2 * Definition for a binary tree node.
3 * struct TreeNode {
4 * int val;
5 * TreeNode *left;
6 * TreeNode *right;
7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {}
8 * };
9 */
10 class Solution {
11 unordered_map<int,vector<int>> e;
12 void setedge(TreeNode* root){
13 if(root->left){
14 e[root->val].push_back(root->left->val);
15 e[root->left->val].push_back(root->val);
16 setedge(root->left);
17 }
18 if(root->right){
19 e[root->val].push_back(root->right->val);
20 e[root->right->val].push_back(root->val);
21 setedge(root->right);
22 }
23 }
24 vector<int> bfs(int init,int k){
25 unordered_set<int> vis;
26 queue<pair<int,int>> q;
27 vector<int> ret;
28 vis.insert(init);
29 q.push({init,0});
30 while(!q.empty()){
31 int u=q.front().first,d=q.front().second;
32 q.pop();
33 if(d>k)break;
34 if(d==k)ret.push_back(u);
35 for(int v:e[u]){
36 if(!vis.count(v)){
37 vis.insert(v);
38 q.push({v,d+1});
39 }
40 }
41 }
42 return ret;
43 }
44 public:
45 vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
46 setedge(root);
47 return bfs(target->val,K);
48 }
49 };
由于每个值都是唯一的,以值为key,左右子节点值以及父节点值组成的vector为value,存储数据,相当于构建了双向链表,从任意点不但能到达孩子节点,还能到达父节点。
然后无论深度优先还是广度优先,都很简单的得到结果了。
对于例子,得到如下邻接表
3:5 1
5:6 2 3
1:3 0 8
6:5
2:5 7 4
0:1
8:1
7:2
4:2
bfs: 5 -> [6 2 3] ->[6:5X]-[2:5X 7 4]-[3:5X 1] ->[7 4 1]
dfs:5 ->[6->5X ] ->[2 ->5X 7 4]->[3 ->5X 1] -> [7 4 1]
1.unordered_map
普通map本身基于红黑树是有序的,unordered_map不需要有序,更看重快速查找
unordered_map容器比映射容器更快地通过它们的键来访问各个元素,尽管它们通过其元素的子集进行范围迭代通常效率较低。
无序映射实现直接访问操作符(operator []),该操作符允许使用其键值作为参数直接访问映射值。
unordered_set与与unordered_map相似
unordered_set是一种无序集合,既然跟底层实现基于hashtable那么它一定拥有快速的查找和删除,添加的优点.基于hashtable当然就失去了基于rb_tree的自动排序功能
unordered_set无序,所以在迭代器的使用上,set的效率会高于unordered_set
参考:
http://www.cplusplus.com/reference/unordered_map/unordered_map/
https://blog.csdn.net/zhc_24/article/details/78915968
https://www.cnblogs.com/LearningTheLoad/p/7565694.html
第三题:翻转急诊后的得分
题目:
有一个二维矩阵 A 其中每个元素的值为 0 或 1 。
移动是指选择任一行或列,并转换该行或列中的每一个值:将所有 0 都更改为 1,将所有 1 都更改为 0。
在做出任意次数的移动后,将该矩阵的每一行都按照二进制数来解释,矩阵的得分就是这些数字的总和。
返回尽可能高的分数。
示例:
输入:[[0,0,1,1],[1,0,1,0],[1,1,0,0]]
输出:39
解释:
转换为 [[1,1,1,1],[1,0,0,1],[1,1,1,1]]
0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39
提示:
1 <= A.length <= 201 <= A[0].length <= 20A[i][j]是0或1
链接:https://leetcode-cn.com/contest/weekly-contest-91/problems/score-after-flipping-matrix/
分析:
1,各个位的权重是不同的,通过行变换将每一行的高位全部变为1
2,然后通过列变换将每一列中的1尽可能的多,其实不需要变换,只需要统计1的个数,如果少于一半,则总数减去1个数即0的个数,也是最终变换后1的个数
3,最终结果不在于每一行组成的数字是多少,而是每一列中的1的和,即1的个数,得到的一个“数”的结果
AC code:
1 class Solution {
2 public:
3 int matrixScore(vector<vector<int>>& A) {
4 if(A.size()==0)
5 {
6 return 0;
7 }
8 //高位权重大,先将所有的最高位设为1,然后每一列尽可能多的设为1
9 int ret=0;
10 //1 最高位设为111
12 for (int i = 0; i < A.size(); i++)
13 {
14 if (A[i][0] == 0)
15 {
16 for (int j = 0; j < A[i].size(); j++)
17 {
18 A[i][j] = 1 - A[i][j]; //0->1 1->0 ^1也行
19 }
20 }
21 }
22 int n = A.size();
23 int m = A[0].size();
24 for (int i = 0; i < A[0].size(); i++)
25 {
26 int counter = 0;
27 for (int j = 0;j<n; j++)
28 {
29 if (A[j][i] == 1)
30 {
31 counter++;
32 }
33 }
34 counter = max(counter, n - counter);
35 ret = ret * 2 + counter;
36 }
37 return ret;
38 }
39
40 };
其他:
用时最少code(0/4ms)
1 class Solution {
2 public:
3
4 int matrixScore(vector<vector<int>>& A) {
5 int ans=0,x=A.size(),y=A[0].size(),n;
6 for(int i=0;i<x;i++){
7 if(A[i][0]==0){
8 for(int j=0;j<y;j++){
9 if(A[i][j]==0) A[i][j]=1;
10 else A[i][j]=0;
11 }
12 }
13 }
14 for(int j=0;j<y;j++){
15 n=0;
16 for(int i=0;i<x;i++){
17 if(A[i][j]==1) n++;
18 }
19 if(n>x/2) ans+=n*pow(2,y-j-1);
20 else ans+=(x-n)*pow(2,y-j-1);
21 }
22 return ans;
23 }
24 };
做法没有区别,时间差异可能在于写法?改用+= power方式后提交执行时间有20/8/4,可能给出的随机测试数据有关?或者后台多个测试server,不同server性能不同?主要目的只是学习,不在深究了。
第四题:和至少为K的最短子数组
题目:
返回 A 的最短的非空连续子数组的长度,该子数组的和至少为 K 。
如果没有和至少为 K 的非空子数组,返回 -1 。
示例 1:
输入:A = [1], K = 1
输出:1
示例 2:
输入:A = [1,2], K = 4
输出:-1
示例 3:
输入:A = [2,-1,2], K = 3
输出:3
提示:
1 <= A.length <= 50000-10 ^ 5 <= A[i] <= 10 ^ 51 <= K <= 10 ^ 9
链接:https://leetcode-cn.com/contest/weekly-contest-91/problems/shortest-subarray-with-sum-at-least-k/
分析:
之前有针对dp进行练习,结果周赛遇到了还是没过……
A:
通过一个结构体数组保存截止到每一个数字的和以及组成该和所用的长度
sum[i]={ A[i],i==0 || sum[i]<0 || A[i]+sum[i-1], i>0&&sum[i-1]>0 }
如果sum[i]-sum[j]>=K(i>j),则找到满足要求的连续区间,然后j尝试增大尽量缩短i-j的值
结果超时了。
1 typedef struct Data
2 {
3 int sum;
4 int length;
5 }Data;
6 class Solution {
7 public:
8 int shortestSubarray(vector<int>& A, int K) {
9 vector<Data> dp(A.size());
10 for (int i = 0; i < A.size(); i++)
11 {
12 if (A[i] >= K)
13 {
14 return 1;
15 }
16
17 if (i == 0)
18 {
19 dp[i].sum = A[i];
20 dp[i].length = 1;
21 }
22 else
23 {
24 if (dp[i - 1].sum <= 0)
25 {
26 dp[i].sum = A[i];
27 dp[i].length = 1;
28 }
29 else
30 {
31 //利用前一个的和和长度,如果和+当前值大于K,按照长度减去前面的值,直到刚好大于K未知,否则-1
32 if (dp[i - 1].sum + A[i] <= K)
33 {
34 dp[i].sum = dp[i - 1].sum + A[i];
35 dp[i].length = dp[i - 1].length+1;
36 }
37 else
38 {
39 //如果大于K,尝试减去前面的值
40 int tmpsum = 0;
41 for (int j = i;j>=0;j--)
42 {
43 tmpsum += A[j];
44 if (tmpsum >= K)
45 {
46 dp[i].sum = tmpsum;
47 dp[i].length = i - j + 1;
48 break;
49 }
50 }
51 }
52 }
53
54 }
55 }
56 int ret = -1;
57 for (int i = 0; i < A.size(); i++)
58 {
59 if (dp[i].sum >= K)
60 {
61 if (ret == -1)
62 {
63 ret = dp[i].length;
64 }else
65 {
66 if (ret > dp[i].length)
67 {
68 ret = dp[i].length;
69 }
70 }
71 }
72 }
73 return ret;
74 }
75 };
后来尝试采用二维数组,通过上三角矩阵的二维vector存储,sums[i][j]表示sum[j]-sum[i]的结果,找到和大于等于K且j-i最小,结果超出内存限制。
1 class Solution {
2 public:
3 int shortestSubarray(vector<int>& A, int K) {
4 if (A.size() == -1)
5 {
6 return -1;
7 }
8 int ret = -1;
9 vector<vector<int>> sums(A.size(), vector<int>(A.size(), 0));
10 for (int i = A.size() - 1; i >= 0;i--)
11 {
12 if (A[i] >= K)
13 {
14 return 1;
15 }
16
17 for (int j = i; j < A.size();j++)
18 {
19 if (i == j)
20 {
21 sums[i][j] = A[i];
22 }
23 else
24 {
25 sums[i][j] = sums[i][j - 1] + A[j];
26 }
27 if (ret==-1 && sums[i][j] >= K)
28 {
29 ret = j - i + 1;
30 }
31 else if (sums[i][j] >= K)
32 {
33 if (ret>j - i + 1)
34 {
35 ret = j - i + 1;
36 }
37 }
38 }
39 }
40
41 return ret;
42 }
43 };
最终放弃治疗直接参考第一code,结合自己理解终于AC(周二晚折腾一晚上,周三晚参考第一code,有一点理解,还是不太懂,不过至少周四晚能够写codeAC), 不过基本“像素级”的参考了……
AC code:
1 class Solution {
2 public:
3 int shortestSubarray(vector<int>& A, int K) {
4 if (A.size() < 1)
5 {
6 return -1;
7 }
8 //按照阅读第一code,自己的理解,尝试独立编程实现
9 //1 <= A.length <= 50000
10 int ret = 50000 + 1; //需要通过min()获取最短长度,但是如果不存在需要将结果返回-1,如果长度还是初始值,说明都没有连续和达到K的
11 vector<pair<int64_t, int64_t>> sums; //后面的是第几个数,前面的是从最开始到该数的和
12 int64_t sum = 0;
13 sums.emplace_back(0, 0); //1.emplace_back 比pushback效率更高 2,先放入(0,0),可以将和为负数的过滤到前面
14 for (int i = 0; i < A.size(); i++)
15 {
16 if (A[i] >= K)
17 {
18 return 1; //如果某个数达到K,则可以直接返回最短长度1
19 }
20 sum += A[i];
21 sums.emplace_back(sum, i+1);
22 }
23 sort(sums.begin(), sums.end()); //按照和进行排序,后面数字是从0到该数字的和,其中额外添加了(0,0),对和不影响
24 //找到以某个数字结尾的最小连续和
25 int left = 0;
26 set<int> tmp; //用来存储能够满足left到i和都满足大于等于K的left
27 for (int i = 0; i <= A.size(); i++)
28 {
29 //由于填充了(0,0),所以第一个不可能是结果(因为排序后第一个要么是0,要么是负数,而且可以优化,如果单个数字大于K,直接返回1)
30 //找到以该数字结尾的符合要求的连续和
31 while (sums[i].first-sums[left].first>=K) //left<K <==> sums[i].first-sums[left].first是正值 sums已经按照first进行了排序
32 {
33 tmp.insert(sums[left].second); //可能存在left.second为开始的一段区间和大于等于K,只要sums[i].second>sums[left].second
34 left++; //sums[left].first 递增,只要当前left满足,前面的left也都满足
35 }
36 //
37 auto it = tmp.lower_bound(sums[i].second); //https://baike.baidu.com/item/lower_bound/8620039?fr=aladdin
38 if (it == tmp.begin())
39 {
40 continue; //如果进来了,说明1,是第一个,2,下标是tmp中最小的,这两种情况都不可能是结果(前面没有sums)
41 }
42 //如果到这里,说明有结果比i小的left
43 //按照前面的分析,前面任意的left都满足要求,而且按照顺序存储的下标,只要和前一个的差值就是满足条件的最小值
44 it--;
45 ret = min(ret, (int)sums[i].second - *it);
46
47 }
48 if (ret == 50000+1)
49 {
50 return -1;
51 }
52 return ret;
53 }
54 };
其他:
1.用时最短code(116/220)
1 class Solution {
2 public:
3 int shortestSubarray(vector<int>& A, int K) {
4 int Ret=50000;
5 deque<int> pq;
6 vector<int> b(A.size()+1);
7 for(int i=0;i<A.size();i++)
8 {
9 b[i+1]+=b[i]+A[i];
10 }
11 for(int i=0;i<b.size();i++)
12 {
13 while(!pq.empty() && b[i]-b[pq.front()]>=K)
14 {
15 Ret = min<int>(Ret,i-pq.front());
16 pq.pop_front();
17 }
18 while(!pq.empty() && b[i]<=b[pq.back()])
19 pq.pop_back();
20 pq.push_back(i);
21 }
22 return Ret==50000?-1:Ret;
23 }
24 };
2.第一的code
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 #define VEVE(i, a, b) for (ll i = a, __##i = b; i < __##i; ++i)
6 #define DYDY(i, a, b) for (ll i = a, __##i = b; i > __##i; --i)
7 #define RARA(x, seq) for (auto &x : seq)
8 #define SIZE(x) ((ll)(x.size()))
9 #define ALL(x) x.begin(), x.end()
10
11 typedef int64_t ll;
12 typedef double dd;
13
14 class Solution {
15 public:
16 int shortestSubarray(vector<int>& A, int K) {
17 ll res = 123456;
18 ll sum = 0;
19 vector<pair<ll, ll>> sums; // (pref sum, idx)
20 sums.emplace_back(sum, 0);
21 VEVE(i, 0, SIZE(A)) {
22 sum += A[i];
23 sums.emplace_back(sum, i + 1);
24 }
25 sort(ALL(sums));
26 ll lef = 0;
27 set<ll> idx;
28 VEVE(i, 0, SIZE(sums)) {
29 while (lef < i and sums[i].first - sums[lef].first >= K) {
30 idx.insert(sums[lef].second);
31 ++lef;
32 }
33 auto it = idx.lower_bound(sums[i].second);
34 if (it == idx.begin())
35 continue;
36 --it;
37 res = min(res, sums[i].second - *it);
38 }
39 if (res == 123456) res = -1;
40 return (int) res;
41 }
42 };
总结:
前三个搞懂了,第四个还是没搞太明白,太晚了,以后有机会在好好研究先第一和用时最短code。
LeetCode之Weekly Contest 91的更多相关文章
- LeetCode之Weekly Contest 102
第一题:905. 按奇偶校验排序数组 问题: 给定一个非负整数数组 A,返回一个由 A 的所有偶数元素组成的数组,后面跟 A 的所有奇数元素. 你可以返回满足此条件的任何数组作为答案. 示例: 输入: ...
- LeetCode之Weekly Contest 92
第一题:转置矩阵 问题: 给定一个矩阵 A, 返回 A 的转置矩阵. 矩阵的转置是指将矩阵的主对角线翻转,交换矩阵的行索引与列索引. 示例 1: 输入:[[1,2,3],[4,5,6],[7,8,9] ...
- LeetCode之Weekly Contest 93
第一题:二进制间距 问题: 给定一个正整数 N,找到并返回 N 的二进制表示中两个连续的 1 之间的最长距离. 如果没有两个连续的 1,返回 0 . 示例 1: 输入:22 输出:2 解释: 22 的 ...
- LeetCode之Weekly Contest 90
LeetCode第90场周赛记录 第一题:亲密字符串 问题: 给定两个由小写字母构成的字符串 A 和 B ,只要我们可以通过交换 A 中的两个字母得到与 B 相等的结果,就返回 true :否则返回 ...
- LeetCode之Weekly Contest 101
前一段时间比较忙,而且做这个对于我来说挺耗时间的,已经间隔了几期的没做总结了,后面有机会补齐.而且本来做这个的目的就是为了防止长时间不做把编程拉下,不在追求独立作出所有题了.以后完赛后稍微尝试下,做不 ...
- LeetCode Weekly Contest 8
LeetCode Weekly Contest 8 415. Add Strings User Accepted: 765 User Tried: 822 Total Accepted: 789 To ...
- Leetcode Weekly Contest 86
Weekly Contest 86 A:840. 矩阵中的幻方 3 x 3 的幻方是一个填充有从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等. 给定一个 ...
- leetcode weekly contest 43
leetcode weekly contest 43 leetcode649. Dota2 Senate leetcode649.Dota2 Senate 思路: 模拟规则round by round ...
- LeetCode Weekly Contest 23
LeetCode Weekly Contest 23 1. Reverse String II Given a string and an integer k, you need to reverse ...
随机推荐
- Junit使用总结
对Junit的使用总结,后期会更新! 1.做自动单元测试用的,在方法前面加一个@Test(准备 一个测试用例),这是必须要加上的. 判定是成功还是失败. 最后是加一个断点,Assert.assertE ...
- 《SQL 进阶教程》 case:在 UPDATE 语句里进行条件分支
1.对当前工资为30万日元以上的员工,降薪10%:2.对当前工资为25万日元以上且不满28万日元的员工,加薪20% update salaries set salary = case when sal ...
- Codeforces 140F(坐标系点对称)
要点 结论:如果坐标系一堆点两两对称于某一重心,则排序后第1个和第n个为一对,以此类推. 枚举所有可能的重心点并check.因为隐藏的点不超过k个,所以点1-k+1都可能跟第n个匹配.对右侧同样适用, ...
- D. Blocks 数学题
Panda has received an assignment of painting a line of blocks. Since Panda is such an intelligent bo ...
- centos6.3搭建FTP服务器图文教程
今天下午不忙,没什么事,看到我大红盟linux版块如此冷清,心不能忍,做了个FTP服务器的搭建教程,大家可以看看, 不会做视频,就图文交叉了,写得不好,望谅解.以后有时间再出一个LNMP的教程. 不磨 ...
- Java中的Validated验证
注意点:在使用@NotBlank时,必须与@Valid配着使用,不然不起作用(出现了很奇怪的现象,我第一次试的时候确实有这情况,但是第二次的时候这情况没了,所以这个说不准) @NotBlank 用在S ...
- IDEA对比文件
和另一个文件对比:右击文件,选择另一个文件 和剪切板的内容对比:右击代码区域
- js监听页面的scroll事件,当移到底部时触发事件
//页面拉到底时自动加载更多 $(window).scroll(function(event){ var wScrollY = window.scrollY; // 当前滚动条位置 var wInne ...
- Web前端体系的脉络结构
Web前端技术由 html.css 和 javascript 三大部分构成,是一个庞大而复杂的技术体系,其复杂程度不低于任何一门后端语言.而我们在学习它的时候往往是先从某一个点切入,然后不断地接触和学 ...
- mui实现图片更换(暂未上传)
页面中有默认的图片,触发type为file的input时,更换图片,这个是mui移动端的项目,算了,不多说,开码 首先,先在html页面中设置样式,样式我就不给了,贴个布局 <div class ...
