[luoguP2762] 太空飞行计划问题（最大权闭合图—最小割—最大流）

传送门

如果将每一个实验和其所对的仪器连一条有向边，那么原图就是一个dag图（有向无环）

每一个点都有一个点权，实验为收益（正数），仪器为花费（负数）。

那么接下来可以引出闭合图的概念了。

闭合图是原图的一个点集，其中这个点集中每个点的出边所指向的点依然在这个点集中，那么这个点集就是个闭合图。

比如论文中的这个图：

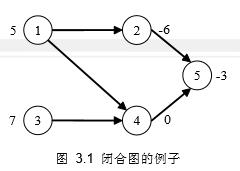
在图 3.1 中的网络有 9 个闭合图（含空集）：∅，{3,4,5}，{4,5}，{5}，{2,4,5}，{2,5}，{2,3,4,5}，{1,2,4,5}，{1,2,3,4,5}

其中有大权和的闭合图是{3,4,5} ，权和为 4。

显然，我们目的就是求原图中的最大权闭合图。

为了求解这个，需要先把该图转化成网络。

增加一个超级原点s，s与每个实验连一条权值为实验利益的边。

增加一个超级汇点t，每个仪器与t连一条权值为仪器花费（正数）的边。

每个实验与它所依靠的仪器连一条权值为INF的边。

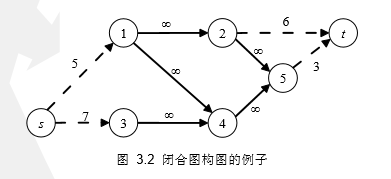
那么所有实验的费用（不是利益）减去最大流（最小割）即为最大的利益。

为什么呢？

根据论文中的证明，可以把最大权闭合图的问题转化为最小割。（然而看不懂）

下面转载一段比较简单的证明（然而还是看不懂）

首先引入结论，最小割所产生的两个集合中，其源点S所在集合(除去S)为最大权闭合图，接下来我们来说明一些结论。

• 证明:最小割为简单割。

引入一下简单割的概念：割集的每条边都与S或T关联。(请下面阅读时一定分清最小割与简单割，容易混淆)

那么为什么最小割是简单割呢？因为除S和T之外的点间的边的容量是正无穷，最小割的容量不可能为正无穷。所以，得证。

• 证明网络中的简单割与原图中闭合图存在一一对应的关系。(即所有闭合图都是简单割，简单割也必定是一个闭合图)。

证明闭合图是简单割：如果闭合图不是简单割(反证法)。那么说明有一条边是容量为正无穷的边，则说明闭合图中有一条出边的终点不在闭合图中，矛盾。

证明简单割是闭合图：因为简单割不含正无穷的边，所以不含有连向另一个集合(除T)的点，所以其出边的终点都在简单割中，满足闭合图定义。得正。

• 证明最小割所产生的两个集合中，其源点S所在集合(除去S)为最大权闭合图。

首先我们记一个简单割的容量为C,且S所在集合为N，T所在集合为M。

则C=M中所有权值为正的点的权值(即S与M中点相连的边的容量)+N中所有权值为负的点权值的绝对值(即N中点与T中点相连边的容量)。记(C=x1+y1);(很好理解，不理解画一个图或

想象一下就明白了)。

我们记N这个闭合图的权值和为W。

则W=N中权值为正的点的权值-N中权值为负的点的权值的绝对值。记(W=x2-y2);

则W+C=x1+y1+x2-y2。

因为明显y1=y2，所以W+C=x1+x2;

x1为M中所有权值为正的点的权值，x2为N中权值为正的点的权值。

所以x1+x2=所有权值为正的点的权值之和(记为TOT).

所以我们得到W+C=TOT.整理一下W=TOT-C.

到这里我们就得到了闭合图的权值与简单割的容量的关系。

　 因为TOT为定值，所以我们欲使W最大，即C最小，即此时这个简单割为最小割，此时闭合图为其源点S所在集合(除去S)。得正。

至此，我们就将最大权闭合图问题转化为了求最小割的问题。求最小割用最小割容量=最大流，即可将问题转化为求最大流的问题。

转载结束。

当然也可以这样理解，任意（非无穷大）割的值的意义都表示　实验集合中所不选的实验的利益 + 仪器集合中所选仪器的花费

那么　所有实验的利益 - 割 = 所有实验的利益 - （实验集合中所不选的实验的利益 + 仪器集合中所选仪器的花费) = 实验集合中所选的实验的利益 - 仪器集合中所选仪器的花费 = 总利益

要使得总利益最大，即使割最小，那么就可以通过求最小割来解决。

至于所选的实验和仪器，只需要找最后一次增广时能够到达的点（即集合S）即可。

——代码

 #include <queue>
 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #define N 3010
 #define min(x, y) ((x) < (y) ? (x) : (y))

 int n, m, sum, cnt, s, t, ans;
 int len[N], num[N][N], dis[N], cur[N];
 int head[N], next[N << ], to[N << ], val[N << ];

 inline int read()
 {
     int x = , f = ;
     char ch = getchar();
     for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = -;
     for(; isdigit(ch); ch = getchar()) x = (x << ) + (x << ) + ch - '';
     return x * f;
 }

 inline void add(int x, int y, int z)
 {
     to[cnt] = y;
     val[cnt] = z;
     next[cnt] = head[x];
     head[x] = cnt++;
 }

 inline bool bfs()
 {
     std::queue <int> q;
     memset(dis, -, sizeof(dis));
     dis[s] = ;
     q.push(s);
     int i, u, v;
     while(!q.empty())
     {
         u = q.front();
         q.pop();
         for(i = head[u]; i ^ -; i = next[i])
         {
             v = to[i];
             if(val[i] && dis[v] == -)
             {
                 dis[v] = dis[u] + ;
                 if(v == t) return ;
                 q.push(v);
             }
         }
     }
     return ;
 }

 inline int dfs(int u, int maxflow)
 {
     if(u == t) return maxflow;
     int i, v, d, ret = ;
     for(i = cur[u]; i ^ -; i = next[i])
     {
         v = to[i];
         if(val[i] && dis[v] == dis[u] + )
         {
             d = dfs(v, min(val[i], maxflow - ret));
             ret += d;
             val[i] -= d;
             val[i ^ ] += d;
             cur[u] = i;
             if(ret == maxflow) return ret;
         }
     }
     return ret;
 }

 int main()
 {
     int i, j, x, l;
     std::string S;
     m = read();
     n = read();
     s = , t = n + m + ;
     memset(head, -, sizeof(head));
     for(i = ; i <= m; i++)
     {
         x = read();
         add(s, i, x);
         add(i, s, );
         sum += x;
         getline(std::cin, S);
         l = S.length();
         for(j = ; j < l; j++)
         {
             x = ;
             if(S[j] == ' ') continue;
             while(isdigit(S[j]))
             {
                 x = (x << ) + (x << ) + S[j] - '';
                 j++;
             }
             num[i][++len[i]] = x;
         }
         for(j = ; j <= len[i]; j++)
             add(i, num[i][j] + m, 1e9), add(num[i][j] + m, i, );
     }
     for(i = ; i <= n; i++)
     {
         x = read();
         add(i + m, t, x);
         add(t, i + m, );
     }
     while(bfs())
     {
         for(i = s; i <= t; i++) cur[i] = head[i];
         ans += dfs(s, 1e9);
     }
     for(i = ; i <= m; i++)
         if(dis[i] ^ -)
             printf("%d ", i);
     puts("");
     for(i = ; i <= n; i++)
         if(dis[i + m] ^ -)
             printf("%d ", i);
     puts("");
     printf("%d\n", sum - ans);
     return ;
 }

转载内容来自：http://www.cnblogs.com/wuyiqi/archive/2012/03/12/2391960.html

参考：胡伯涛 《最小割模型在信息学竞赛中的应用》