6.17考试总结(NOIP模拟8)[星际旅行·砍树·超级树·求和]

6.17考试总结(NOIP模拟8)

背景

考得不咋样，有一个非常遗憾的地方:最后一题少取膜了，\(100pts->40pts\)，改了这么多年的错还是头一回看见以下的情景。。。

T1星际旅行

前言

考试的时候用一个自己感觉非常妙的思路骗了20pts，因为是双向边，所以分成两个边存，边的tot从2开始，这样可以保证没一组边的序号通过取\(xor\)可以相互转化。

然后对于每一个边记录经过次数，并且记一下经过次数为1和2的边的总数，然后对于dfs时转移的就是状压的每组边的状态，当然也可以拿Hash存。

做法挺妙的，唯一的缺点就是和正解一点关系都没有（逃

解题思路

正解主要是欧拉路的相关知识。

首先可以确定的是，如果这个图里面的各个边不是联通的话（可以用冰茶几或者DFS来判），那么总情况数一定是0，比如下图的情况：

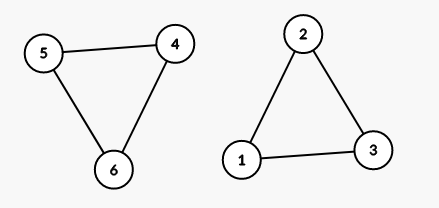
然后就是建立在欧拉路以及欧拉回路上面的东西了，

存在欧拉路的条件：图是连通的，有且只有2个奇点。

存在欧拉回路的条件：图是连通的，有0个奇点。

因此，问题就变成了把所有的边变成两条边之后，拆掉两条边使得新图仍然具有联通性，设自环数为\(cnt\)，每个点的出入度为\(du[i]\)，主要分为一下三种情况：

• 去掉任意2个自环：情况数为\(\dfrac{cnt\times(cnt-1)}{2}\)
• 去掉一个自环和一条边：情况数为：\(\dfrac{cnt \times \sum\limits_{i=1}^ndu_i}{2}\)
• 去掉两个有公共点的边：情况数为\(\dfrac{\sum\limits_{i=1}^n du_i \times (du_i-1)}{2}\)

记得开long long

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10,M=N<<1;
int n,m,link=N-1,sum,sum1,sum2,sum3,du[N],rdu[N],fa[N];
int find(int x)
{
	if(fa[x]==x)
		return x;
	return fa[x]=find(fa[x]);
}
#undef int
int main()
{
	#define int register long long
	#define ll long long
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++)
		fa[i]=i;
	for(int i=1,x,y;i<=m;i++)
	{
		scanf("%lld%lld",&x,&y);
		if(x==y)
		{
			sum++;
			rdu[x]++;
			rdu[y]++;
			continue;
		}
		du[x]++;
		du[y]++;
		rdu[x]++;
		rdu[y]++;
		x=find(x);
		y=find(y);
		fa[x]=y;
	}
	for(int i=1;i<=n;i++)
		if(rdu[i])
		{
			link=i;
			find(i);
			break;
		}
	for(int i=1;i<=n;i++)
		if(rdu[i]&&find(i)!=fa[link])
		{
			printf("0");
			return 0;
		}
	sum1=sum*(sum-1)/2;
	for(int i=1;i<=n;i++)
	{
		sum2+=du[i];
		sum3+=du[i]*(du[i]-1)/2;
	}
	sum2=sum2*sum/2;
	printf("%lld",sum1+sum2+sum3);
	return 0;
}

T2 砍树

前言

考试的时候想到了二分答案，以为自己要切题了，然后考试结束前20分钟的时候突然就搞出来一个反例，不满足单调性，但是时间又不够了，我就草草的在错误答案的基础上改了一下，骗了20pts

解题思路

首先说一下为什么不满足单调性，显然的天数与希望树木的高度是有倍数关系的。。

问题就是让我们求一个最大的\(d\)，满足：

\[\sum\limits_{i=1}^n(\lceil \dfrac{a_i}{d}\rceil \times d-a_i)\le k
\]

移一下项，令\(T=k+\sum\limits_{i=1}^na_i\),可得：

\[\sum\limits_{i=1}^n\lceil \dfrac{a_i}{d}\rceil \times d\le T
\]

\[\sum\limits_{i=1}^n\lceil \dfrac{a_i}{d}\rceil \le \dfrac{T}{d}
\]

\[\sum\limits_{i=1}^n\lceil \dfrac{a_i}{d}\rceil \le \lfloor \dfrac{T}{d} \rfloor
\]

然后我们就可以愉快的整除分块，暴力枚举每一个d然后判断是否符合条件就好了，显然的，对于每一个块里，右端点是最优解。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=110;
int n,m,ans,temp,s[N];
#undef int
int main()
{
	#define int register long long
	#define ll long long
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%lld",&s[i]);
	for(int i=1;i<=n;i++)
		temp+=s[i];
	temp+=m;
	for(int l=1,r;l<=temp;l=r+1)
	{
		r=temp/(temp/l);
		int sum=0;
		for(int i=1;i<=n;i++)
			sum+=ceil(1.0*s[i]/(1.0*r));
		if(sum<=temp/r)
			ans=r;
	}
	printf("%lld",ans);
	return 0;
}

T3 超级树

前言

挺难的一道题，我考场上几乎是直接输出的样例，5pts，不知道是根据dp方程出的题还是出题人真的太强了，想出来的。。。

解题思路

首先要明白dp数组的含义：

dp[i][j]表示一棵i-超级树，有j条点不重复的路径的方案数

何为j条点不重复的路径？

在j条路径中，各个路径没有相交的部分（相同的点）。

考虑从dp[i]转移到dp[i+1]，有五种转移状态

• 什么也不做：\(dp[i+1][l+r]+=num\)

• 根自己作为一条新路径 \(dp[i+1][l+r+1]+=num\)

• 根连接到左子树（或右子树）的某条路径上 \(dp[i+1][l+r]+=2 \times num \times (l+r)\)

• 根连接左子树和右子树的各一条路径 \(dp[i+1][l+r-1]+=2 \times num \times l\times r\)

• 根连接左子树（或右子树）的两条路径 \(dp[i+1][l+r-1]+=num \times (l \times (l-1)+r \times (r-1))\)

边界为dp[1][0]=dp[1][1]=1，答案为dp[k][1]。

看起来第二维状态可能有\(2^k\)那么大，但注意到从dp[i]转移到dp[i+1]时，路径的条数最多减少1条，因此第二维只有k个状态对最终的状态有影响，只dp这些状态即可。

• 注意：取\(\bmod\)运算不要太多，否则会TLE

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=610;
int n,mod,f[N][N];
#undef int
int main()
{
	#define int register long long
	#define ll long long
	scanf("%lld%lld",&n,&mod);
	f[1][0]=f[1][1]=1;
	for(int dep=1;dep<n;dep++)
		for(int i=0;i<=n;i++)
			for(int j=0;j<=n-i;j++)
			{
				int num=f[dep][i]*f[dep][j]%mod;
				f[dep+1][i+j]=(f[dep+1][i+j]+num)%mod;
				f[dep+1][i+j+1]=(f[dep+1][i+j+1]+num)%mod;
				f[dep+1][i+j]=(f[dep+1][i+j]+2*num*(i+j))%mod;
				f[dep+1][i+j-1]=(f[dep+1][i+j-1]+2*num*i*j)%mod;
				f[dep+1][i+j-1]=(f[dep+1][i+j-1]+num*(i*(i-1)+j*(j-1)))%mod;
			}
	printf("%lld",f[n][1]%mod);
	return 0;
}

P4427 [BJOI2018]求和

前言

就这板子题，我竟然没有赛场上切掉，还是太菜了。。

解题思路

比较简单，先处理一下各种k次方，在搞一下深度的前缀和，剩下的就是LCA了（倍增，Tarjan，树链剖分都可以），当然也可以直接暴力向上跳，至于为什么又快又对，就非常玄学了。。。

• 注意：取\(\bmod\)要到位

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+10,M=N<<1,mod=998244353;
int n,Q,dep[N],f[N][25],q[51][N],po[N][51];
int tot,head[N],nxt[M],ver[M];
void add_edge(int x,int y)
{
	ver[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
}
int ksm(int x,int y)
{
	int temp=1;
	while(y)
	{
		if(y&1)
			temp=temp*x%mod;
		y>>=1;
		x=x*x%mod;
	}
	return temp;
}
void dfs(int x,int fa)
{
	for(int i=head[x];i;i=nxt[i])
	{
		int to=ver[i];
		if(to==fa)
			continue;
		dep[to]=dep[x]+1;
		f[to][0]=x;
		dfs(to,x);
	}
}
void LCA_init()
{
	dfs(1,0);
	for(int j=1;j<=20;j++)
		for(int i=1;i<=n;i++)
			f[i][j]=f[f[i][j-1]][j-1];
}
int LCA_ask(int x,int y)
{
	if(x==y)
		return x;
	if(dep[x]>dep[y])
		swap(x,y);
	for(int i=20;i>=0;i--)
		if(dep[x]<=dep[f[y][i]])
			y=f[y][i];
	if(x==y)
		return x;
	for(int i=20;i>=0;i--)
		if(f[x][i]!=f[y][i])
		{
			x=f[x][i];
			y=f[y][i];
		}
	return f[x][0];
}
#undef int
int main()
{
	#define int register long long
	#define ll long long
	scanf("%lld",&n);
	for(int i=1,x,y;i<n;i++)
	{
		scanf("%lld%lld",&x,&y);
		add_edge(x,y);
		add_edge(y,x);
	}
	LCA_init();
	for(int i=1;i<=n;i++)
	{
		po[i][0]=1;
		for(int j=1;j<=50;j++)
			po[i][j]=po[i][j-1]*i%mod;
	}
	for(int i=0;i<=50;i++)
		for(int j=1;j<=n;j++)
			q[i][j]=(q[i][j-1]+po[j][i])%mod;
	scanf("%lld",&Q);
	while(Q--)
	{
		int x,y,k,lca;
		scanf("%lld%lld%lld",&x,&y,&k);
		lca=LCA_ask(x,y);
		printf("%lld\n",(((q[k][dep[x]]+q[k][dep[y]])%mod-q[k][dep[lca]]+mod)%mod-q[k][dep[f[lca][0]]]+mod)%mod);
	}
	return 0;
}