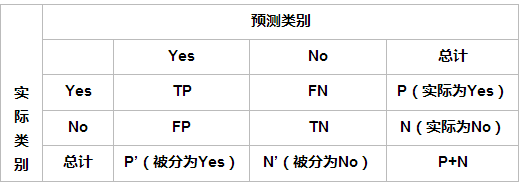
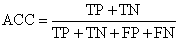机器学习算法中的评价指标（准确率、召回率、F值、ROC、AUC等）

参考链接：https://www.cnblogs.com/Zhi-Z/p/8728168.html

具体更详细的可以查阅周志华的西瓜书第二章，写的非常详细~

一、机器学习性能评估指标

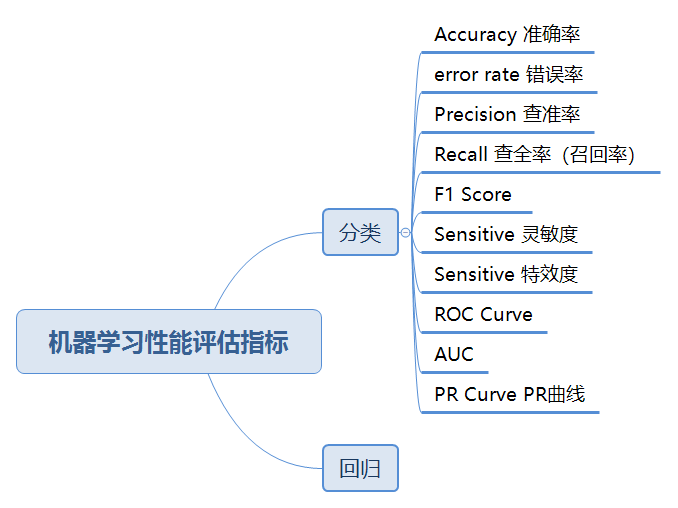
1.准确率(Accurary)

准确率是我们最常见的评价指标，而且很容易理解，就是被分对的样本数除以所有的样本数，通常来说，正确率越高，分类器越好。

准确率确实是一个很好很直观的评价指标，但是有时候准确率高并不能代表一个算法就好。比如某个地区某天地震的预测，假设我们有一堆的特征作为地震分类的属性，类别只有两个：0：不发生地震、1：发生地震。一个不加思考的分类器，对每一个测试用例都将类别划分为0，那那么它就可能达到99%的准确率，但真的地震来临时，这个分类器毫无察觉，这个分类带来的损失是巨大的。为什么99%的准确率的分类器却不是我们想要的，因为这里数据分布不均衡，类别1的数据太少，完全错分类别1依然可以达到很高的准确率却忽视了我们关注的东西。再举个例子说明下。在正负样本不平衡的情况下，准确率这个评价指标有很大的缺陷。比如在互联网广告里面，点击的数量是很少的，一般只有千分之几，如果用acc，即使全部预测成负类（不点击）acc也有 99% 以上，没有意义。因此，单纯靠准确率来评价一个算法模型是远远不够科学全面的。

2、错误率（Error rate）

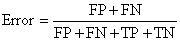
错误率则与准确率相反，描述被分类器错分的比例，对某一个实例来说，分对与分错是互斥事件，所以accuracy =1 - error rate。

3、查准率（Precision）

查准率(precision)定义为：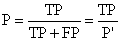 

表示被分为正例的示例中实际为正例的比例。

4、查全率（召回率）（recall）

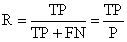
召回率是覆盖面的度量，度量有多个正例被分为正例，recall=TP/(TP+FN)=TP/P=sensitive，可以看到召回率与灵敏度是一样的。

5、综合评价指标（F-Measure）

P和R指标有时候会出现的矛盾的情况，这样就需要综合考虑他们，最常见的方法就是F-Measure（又称为F-Score）。 F-Measure是Precision和Recall加权调和平均： 
 

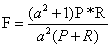
当参数α=1时，就是最常见的F1，也即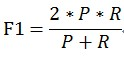 
 
可知F1综合了P和R的结果，当F1较高时则能说明试验方法比较有效。

6、灵敏度（sensitive）

sensitive = TP/P，表示的是所有正例中被分对的比例，衡量了分类器对正例的识别能力。

7、特效度（sensitive）

specificity = TN/N，表示的是所有负例中被分对的比例，衡量了分类器对负例的识别能力。

8、其他评价指标

8.1 ROC曲线

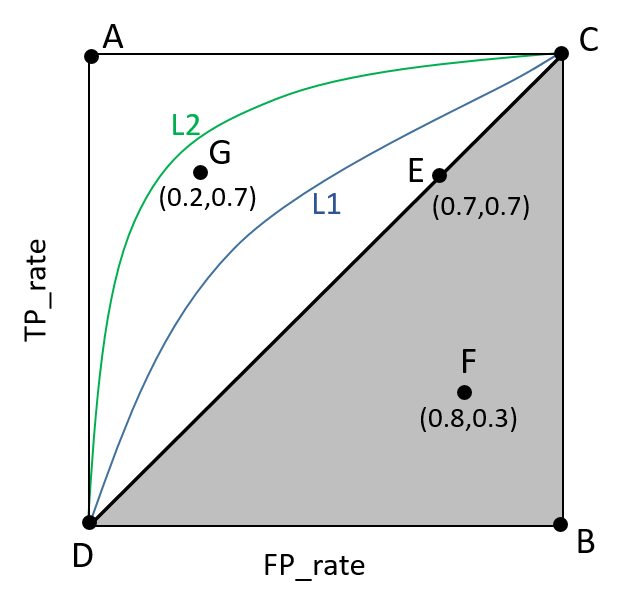
ROC（Receiver Operating Characteristic）曲线是以假正率（FP_rate）和真正率（TP_rate）为轴的曲线，ROC曲线下面的面积我们叫做AUC，如下图所示

，

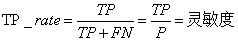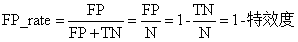
（1）曲线与FP_rate轴围成的面积（记作AUC）越大，说明性能越好，即图上L2曲线对应的性能优于曲线L1对应的性能。即：曲线越靠近A点（左上方）性能越好，曲线越靠近B点（右下方）曲线性能越差。 
（2）A点是最完美的performance点，B处是性能最差点。 
（3）位于C-D线上的点说明算法性能和random猜测是一样的，如C、D、E点；位于C-D之上（曲线位于白色的三角形内）说明算法性能优于随机猜测，如G点；位于C-D之下（曲线位于灰色的三角形内）说明算法性能差于随机猜测，如F点。 
（4）虽然ROC曲线相比较于Precision和Recall等衡量指标更加合理，但是其在高不平衡数据条件下的的表现仍然不能够很好的展示实际情况。

8.2、PR曲线： 
即，PR（Precision-Recall），以查全率为横坐标，以查准率为纵坐标的曲线。 
举个例子（例子来自Paper：Learning from eImbalanced Data）：

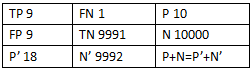
假设N>>P（即Negative的数量远远大于Positive的数量），就算有较多N的sample被预测为P，即FP较大为9，但是由于N很大，FP_rate的值仍然可以很小0.9%，TP_rate=90%（如果利用ROC曲线则会判断其性能很好，但是实际上其性能并不好），但是如果利用PR，P=50%，R=90%，因此在极度不平衡的数据下（Positive的样本较少），PR曲线可能比ROC曲线更实用。