LSM树——LSM 将B+树等结构昂贵的随机IO变的更快，而代价就是读操作要处理大量的索引文件(sstable)而不是一个，另外还是一些IO被合并操作消耗。

Basic Compaction

为了保持LSM的读操作相对较快，维护并减少sstable文件的个数是很重要的，所以让我们更深入的看一下合并操作。这个过程有一点儿像一般垃圾回收算法。

当一定数量的sstable文件被创建，例如有5个sstable，每一个有10行，他们被合并为一个50行的文件（或者更少的行数）。这个过程一 直持续着，当更多的有10行的sstable文件被创建，当产生5个文件时，它们就被合并到50行的文件。最终会有5个50行的文件，这时会将这5个50 行的文件合并成一个250行的文件。这个过程不停的创建更大的文件。像下图：

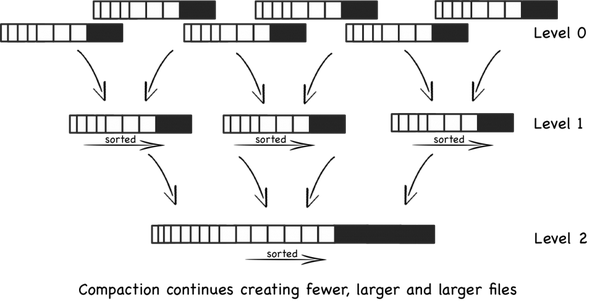
上述的方案有一个问题，就是大量的文件被创建，在最坏的情况下，所有的文件都要搜索。

Levelled Compaction

更新的实现，像 LevelDB 和 Cassandra解决这个问题的方法是：实现了一个分层的，而不是根据文件大小来执行合并操作。这个方法可以减少在最坏情况下需要检索的文件个数，同时也减少了一次合并操作的影响。

按层合并的策略相对于上述的按文件大小合并的策略有二个关键的不同：

1. 每一层可以维护指定的文件个数，同时保证不让key重叠。也就是说把key分区到不同的文件。因此在一层查找一个key，只用查找一个文件。第一层是特殊情况，不满足上述条件，key可以分布在多个文件中。
2. 每次，文件只会被合并到上一层的一个文件。当一层的文件数满足特定个数时，一个文件会被选出并合并到上一层。这明显不同与另一种合并方式：一些相近大小的文件被合并为一个大文件。

这些改变表明按层合并的策略减小了合并操作的影响，同时减少了空间需求。除此之外，它也有更好的读性能。但是对于大多数场景，总体的IO次数变的更多，一些更简单的写场景不适用。

总结

所以， LSM 是日志和传统的单文件索引（B+ tree，Hash Index）的中立，他提供一个机制来管理更小的独立的索引文件(sstable)。

通过管理一组索引文件而不是单一的索引文件，LSM 将B+树等结构昂贵的随机IO变的更快，而代价就是读操作要处理大量的索引文件(sstable)而不是一个，另外还是一些IO被合并操作消耗。

如果还有不明白的，这还有一些其它的好的介绍。

http://leveldb.googlecode.com/svn/trunk/doc/impl.html

and here

关于 LSM 的一些思考

为什么 LSM 会比传统单个树结构有更好的性能？

我们看到LSM有更好的写性能，同时LSM还有其它一些好处。 sstable文件是不可修改的，这让对他们的锁操作非常简单。一般来说，唯一的竞争资源就是 memtable，相对来说需要相对复杂的锁机制来管理在不同的级别。

所以最后的问题很可能是以写为导向的压力预期如何。如果你对LSM带来的写性能的提高很敏感，这将会很重要。大型互联网企业似乎很看中这个问题。 Yahoo 提出因为事件日志的增加和手机数据的增加，工作场景为从 read-heavy 到 read-write。。许多传统数据库产品似乎更青睐读优化文件结构。

因为可用的内存的增加，通过操作系统提供的大文件缓存，读操作自然会被优化。写性能（内存不可提高）因此变成了主要的关注点，所以采取其它的方法，硬件提升为读性能做的更多，相对于写来说。因此选择一个写优化的文件结构很有意义。

理所当然的，LSM的实现，像LevelDB和Cassandra提供了更好的写性能，相对于单树结构的策略。

Beyond Levelled LSM

这有更多的工作在LSM上， Yahoo开发了一个系统叫作 Pnuts， 组合了LSM与B树，提供了更好的性能。我没有看到这个算法的开放的实现。 IBM和Google也实现了这个算法。也有相关的策略通过相似的属性，但是是通过维护一个拱形的结构。如 Fractal Trees， Stratified Trees.

这当然是一个选择，数据库利用大量的配置，越来越多的数据库为不同的工作场景提供插件式引擎。 Parquet 是一个流行的HDFS的替代，在很多相对的文面做的好很（通过一个列格式提高性能）。MySQL有一个存储抽象，支持大量的存储引擎的插件，例如 Toku (使用 fractal tree based index)。

Mongo3.0 则包含了支持B+和LSM的 Wired Tiger引擎。许多关系数据库可以配置索引结构，使用不同的文件格式。

考虑被使用的硬件，昂贵的SSD，像FusionIO有更好的随机写性能，这适合本地更新的策略方法。更便宜的SSD和机械盘则更适合LSM。

延伸阅读

• There is a nice introductory post

  https://www.igvita.com/2012/02/06/sstable-and-log-structured-storage-leveldb/.
  

• The LSM description in this

  http://www.eecs.harvard.edu/~margo/cs165/papers/gp-lsm.pdf
  

  is great and it also discusses interesting extensions.

• These three posts provide a holistic coverage of the algorithm:

  http://leveldb.googlecode.com/svn/trunk/doc/impl.html, http://www.datastax.com/dev/blog/leveled-compaction-in-apache-cassandra and http://www.quora.com/How-does-the-Log-Structured-Merge-Tree-work.
  

• The original Log Structured Merge Tree pape

  r http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.44.2782&rep=rep1&type=pdf
  

  . It is a little hard to follow in my opinion.

• The Big Table paper

  http://static.googleusercontent.com/media/research.google.com/en/archive/bigtable-osdi06.pdf
  

  is excellent.

• http://highscalability.com/blog/2014/8/6/tokutek-white-paper-a-comparison-of-log-structured-merge-lsm.html
  

  on High Scalability.

• Recent work on

  http://researcher.ibm.com/researcher/files/us-wtan/DiffIndex-EDBT14-CR.pdf
  

  which builds on the LSM concept.

• http://blog.empathybox.com/post/24415262152/ssds-and-distributed-data-systems
  

  on SSDs and the benefits of LSM

来自：

http://lcblog.sinaapp.com/?p=223