【BZOJ3675】【APIO2014】序列分割 [斜率优化DP]

序列分割

Time Limit: 40 Sec  Memory Limit: 128 MB
[Submit][Status][Discuss]

Description

　　小H最近迷上了一个分隔序列的游戏。在这个游戏里，小H需要将一个长度为n的非负整数序列分割成k+1个非空的子序列。为了得到k+1个子序列，小H需要重复k次以下的步骤：

　　1.小H首先选择一个长度超过1的序列（一开始小H只有一个长度为n的序列——也就是一开始得到的整个序列）；

　　2.选择一个位置，并通过这个位置将这个序列分割成连续的两个非空的新序列。

　　每次进行上述步骤之后，小H将会得到一定的分数。这个分数为两个新序列中元素和的乘积。小H希望选择一种最佳的分割方式，使得k轮之后，小H的总得分最大。

Input

　　输入第一行包含两个整数n，k（k+1≤n）。
　　第二行包含n个非负整数a1，a2，...，an（0≤ai≤10^4），表示一开始小H得到的序列。

Output

　　输出第一行包含一个整数，为小H可以得到的最大分数。

Sample Input

　　7 3
　　4 1 3 4 0 2 3

Sample Output

　　108

　　在样例中，小H可以通过如下3轮操作得到108分：
　　1．开始小H有一个序列(4，1，3，4，0，2，3)。
　　小H选择在第1个数之后的位置将序列分成两部分，并得到4×(1+3+4+0+2+3)=52分。
　　2．这一轮开始时小H有两个序列：(4)，(1，3，4，0，2，3)。
　　小H选择在第3个数字之后的位置将第二个序列分成两部分，并得到(1+3)×(4+0+2+3)=36分。
　　3．这一轮开始时小H有三个序列：(4)，(1，3)，(4，0，2，3)。
　　小H选择在第5个数字之后的位置将第三个序列分成两部分，并得到(4+0)×(2+3)=20分。
　　经过上述三轮操作，小H将会得到四个子序列：(4)，(1，3)，(4，0)，(2，3)并总共得到52+36+20=108分。

HINT

　　2≤n≤100000 , 1≤k≤min(n -1，200)。

Main idea

　　将一个序列分成k段，定义权值和为两两段的累加和的乘积，求出最大权值和。

Source

　　首先发现n<=10^5,k<=200，我们先想这应该是一道DP，然后发现了原题中的操作（每次分为两段然后再分）经过分配是可以转化为题意这样的，这样的话答案就与分的顺序无关了。
　　一开始我想到了一个O(n^3*k)的做法，每次分割出i~j段，然后发现由于与顺序无关这个性质，可以转化成每次分割第i个位置， 那么我们得到了状态：f[a][i]表示分割第a次，第a次在第i个位置分的答案。
　　然后立马想到了转移方程：f[a][i]=max(f[a][i],f[a-1][j]+s[j]*(s[i]-s[j])) (其中s[i]表示1~i的和)，这样的话效率是O(n^2*k)，然后我们考虑如何优化。大胆猜测可以使用斜率优化。
　　首先假定k<j，且j的决策更优，那么使得条件成立的式子(以下f[j]表示f[a-1][j])：

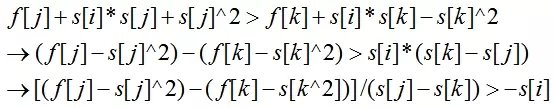
　　令x[i]表示f[a-1][i]-s[i]*s[i]，y[i]表示s[i]，该式子即可表示为：(x[j]-x[k]) / (y[j]-y[k]) > -s[i]。
　　然后斜率优化维护一下上凸壳(取max值)即可，效率即为O(n*k)。
　　注意一下内存限制128MB，所以我们将第一维a滚动即可，由于用的是斜率优化维护凸壳，所以我们一开始需要将a[i]=0的去掉否则答案会偏小。

　　PS：
　　总结一下斜率优化推式子的精髓：假定k<j且j的决策更优，然后列出不等式，去掉只与i有关的项（这时候可能存在s[j]*s[i]这种项式），然后将不等式移项，使得不等号右边仅有与s[i]有关的项（即与j,k无关），然后根据最大值或者最小值决定维护上凸壳或下凸壳。

Code

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;  

 const int ONE=;

 int T,n,m;
 int a[ONE];
 int tou,wei;
 long long s[ONE];
 long long f[][ONE];
 int q[ONE];

 int get()
 {
         int res=,Q=;char c;
         while( (c=getchar())< || c> )
         if(c=='-')Q=-;
         res=c-;
         while( (c=getchar())>= && c<= )
         res=res*+c-;
         return res*Q;
 }

 double slope(int a,int j,int k)
 {
         double xj,xk,yj,yk;
         xj=f[!a][j]-s[j]*s[j];  xk=f[!a][k]-s[k]*s[k];
         yj=s[j];    yk=s[k];
         return (xj-xk)/(yj-yk);
 }

 int main()
 {
     //  freopen("s.in","r",stdin);
         //freopen("s.out","w",stdout);
         T=get();    m=get();

         int begin=;
         for(int i=;i<=T;i++)
         {
             a[i]=get();
             if(a[i]) a[++n]=a[i];
         }
         for(int i=;i<=n;i++) s[i]=s[i-]+a[i];

         int A=,B=,jishu=;
         for(int a=;a<=m;a++)
         {
             swap(A,B);
             tou=wei=;
             for(int i=;i<=n;i++)
             {
                 while(tou<wei && slope(B,q[wei],q[wei-]) < slope(B,i,q[wei])) wei--;
                 q[++wei]=i;

                 while(tou<wei && slope(B,q[tou+],q[tou]) > -s[i]) tou++;

                 f[B][i]=max(f[B][i],f[A][q[tou]] + s[i]*s[q[tou]] - s[q[tou]]*s[q[tou]] );
             }
         }

         printf("%lld",f[B][n]);
 }