算法学习——kruskal重构树
kruskal重构树是一个比较冷门的数据结构。
其实可以看做一种最小生成树的表现形式。
在普通的kruskal中,如果一条边连接了在2个不同集合中的点的话,我们将合并这2个点所在集合。
而在kruskal重构树中,如果一条边连接了在2个不同集合中的点,我们将新建一个节点出来,并用这个新节点作为一个中转连接这2个集合。
如图就是一棵kruskal重构树,方点表示新建出的节点,圆点是原图中的点,方点点权即边权。
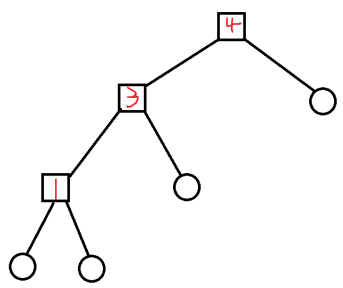
这样建出的树会有一些美妙的性质,例如往上走点权是递增的,原图中的每个点都是叶子节点等。
当然一个更重要的是,如果我们要在最小生成树上求一些东西,这些建出的方点可以给我们提供方向。
原因就是我们每次都将新建的节点作为父亲,那么这些节点将会引导每个原图中的节点一步步向上,从而形成一个有根树,而且由于每个点被新建出的顺序将直接决定它的深度等信息,这棵树会有很多奇妙的性质。
例如我们可以一直向上走,找到某个节点使得这个节点即以下的点都满足点权小于k,这样我们就可以筛选出满足互相到达不会经过超过k的权值的边的点对。
当然也可以有别的用法,于是我们就可以快速的筛选出最小生成树上满足具有某些性质的节点。
同时kruskal重构树也将平时隐藏在并查集里的一些关系提出来放在了树里,因此也可以看做kruskal重构树其实是维护了一个类似并查集的关系
算法学习——kruskal重构树的更多相关文章
- [算法模板]Kruskal重构树
[算法模板]Kruskal重构树 kruskal重构树是一个很常用的图论算法.主要用于解决u->v所有路径上最长边的最小值,就是找到\(u->v\)的一条路径,使路径上的最长边最小. 图片 ...
- 【NOI 2018】归程(Kruskal重构树)
题面在这里就不放了. 同步赛在做这个题的时候,心里有点纠结,很容易想到离线的做法,将边和询问一起按水位线排序,模拟水位下降,维护当前的各个联通块中距离$1$最近的距离,每次遇到询问时输出所在联通块的信 ...
- kruskal重构树学习笔记
\(kruskal\) 重构树学习笔记 前言 \(8102IONCC\) 中考到了,本蒟蒻不会,所以学一下. 前置知识 \(kruskal\) 求最小(大)生成树,树上求 \(lca\). 算法详 ...
- 【学习笔记】Kruskal 重构树
1. 例题引入:BZOJ3551 用一道例题引入:BZOJ3551 题目大意:有 \(N\) 座山峰,每座山峰有他的高度 \(h_i\).有些山峰之间有双向道路相连,共 \(M\) 条路径,每条路径有 ...
- Kruskal重构树学习笔记+BZOJ3732 Network
今天学了Kruskal重构树,似乎很有意思的样子~ 先看题面: BZOJ 题目大意:$n$ 个点 $m$ 条无向边的图,$k$ 个询问,每次询问从 $u$ 到 $v$ 的所有路径中,最长的边的最小值. ...
- [学习笔记]kruskal重构树 && 并查集重构树
Kruskal 重构树 [您有新的未分配科技点][BZOJ3545&BZOJ3551]克鲁斯卡尔重构树 kruskal是一个性质优秀的算法 加入的边是越来越劣的 科学家们借这个特点尝试搞一点事 ...
- [luogu P4197] Peaks 解题报告(在线:kruskal重构树+主席树 离线:主席树+线段树合并)
题目链接: https://www.luogu.org/problemnew/show/P4197 题目: 在Bytemountains有N座山峰,每座山峰有他的高度$h_i$.有些山峰之间有双向道路 ...
- Kruskal重构树入门
这个知识点好像咕咕咕了好长了..趁还没退役赶紧补一下吧.. 讲的非常简略,十分抱歉.. 前置知识 Kruskal算法 一定的数据结构基础(如主席树) Kruskal重构树 直接bb好像不是很好讲,那就 ...
- 【BZOJ】3732: Network【Kruskal重构树】
3732: Network Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 2812 Solved: 1363[Submit][Status][Dis ...
随机推荐
- YII2.0 获取当前访问地址/IP信息
假设我们当前页面的访问地址是:http://localhost/CMS/public/index.php?r=news&id=1 一. 1.获取当前域名:echo Yii::app()-> ...
- Hadoop(21)-数据清洗(ELT)简单版
有一个诸如这样的log日志 去除长度不合法,并且状态码不正确的记录 LogBean package com.nty.elt; /** * author nty * date time 2018-12- ...
- javaweb 项目部署到tomcat
1.准备环境 1.安装 mysql 2.安装java 环境 3.使用idea打war包 点击 apply 生成war包 将war包传到tomcat的webapp目录下,进入tomcat安装目录,进入b ...
- node Cookie
代码: const express = require('express'); const cookieParser = require('cookie-parser'); const app = e ...
- go学习笔记-语言指针
语言指针 定义及使用 变量是一种使用方便的占位符,用于引用计算机内存地址.取地址符是 &,放到一个变量前使用就会返回相应变量的内存地址. 一个指针变量指向了一个值的内存地址.类似于变量和常量, ...
- (数据科学学习手札36)tensorflow实现MLP
一.简介 我们在前面的数据科学学习手札34中也介绍过,作为最典型的神经网络,多层感知机(MLP)结构简单且规则,并且在隐层设计的足够完善时,可以拟合任意连续函数,而除了利用前面介绍的sklearn.n ...
- html中显示指数、底数
在web前端开发中,经常要显示指数.底数,比如x2,loga,我们可以使用span标签,通过控制标签内字体大小,对齐方式来实现想要的效果.代码如下 <table> <tr> & ...
- WebService第一天——概述与入门操作
一.概述 1.是什么 Web service是一个平台独立的,低耦合的,自包含的.基于可编程的web的应用程序,可使用开放的XML(标准通用标记语言下的一个子集)标准来描述.发布.发现.协调和配置这些 ...
- WPF中,如何将Vista Aero效果扩展到整个窗口
原文:WPF中,如何将Vista Aero效果扩展到整个窗口 WPF中,如何将Vista Aero效果扩展到整个窗口 ...
- java反射操作类方法与属性
package com.fanshe.test; public class User { private int age; private String email; private String u ...
