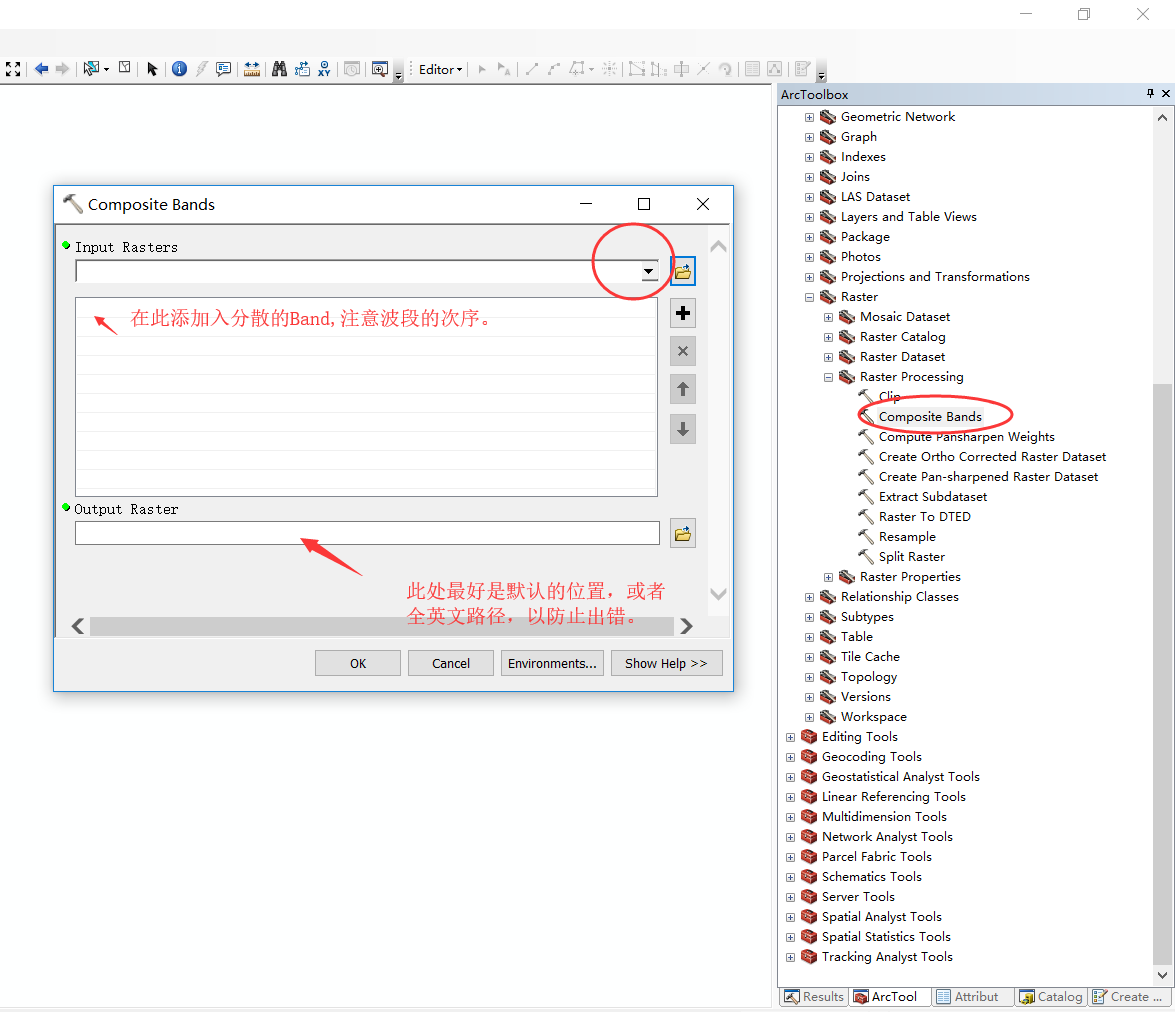
此处用到了ArcGIS栅格处理中的Composite Bands工具（ Data Management Tools --> Raster --> Raster Processing）。具体操作如下图所示。

ArcGIS中的多个栅格波段合成一幅影像的更多相关文章

  1. arcgis中栅格矢量计算技巧收藏

    ​ ​编辑 一.计算面积 ( 可以帮我们计算小班面积 )添加 AREA 字段,然后右键点击字段列,然后点击 CALCULATE VALUES; ---> 选择 ADVANCED -->把下 ...

  2. ArcGIS中重采样栅格像元对齐问题

    转发自我的知乎文章 我们通常要进行基于像元的运算,往往我们的研究中涉及到多源数据,因此就需要对数据进行地理配准.空间配准.重采样等操作. 一开始,我认为相同的地理椭球与投影坐标系下,不同来源,不同分辨 ...

  3. ArcGIS中的影像色彩校正（转）

    ArcGIS中的影像色彩校正 在遥感影像处理工作中,影像镶嵌是最常用影像处理方式之一,关于影像镶嵌的相关功能,在ArcGIS中有多种实现途径,如使用Mosaic工具.创建镶嵌数据集来进行虚拟镶嵌等等. ...

  4. ArcGIS中的坐标系：基本概念和常用操作（一）

    本文呢是主要是借鉴李郎平李大大的博士论文和百度百科,里面还有一点点我自己的理解,希望能帮助自己加深对于坐标系的认识. 李大大的博客:http://blog.sciencenet.cn/u/Brume ...

  5. arcgis中的geodatabase模型

    简介Geodatabase是ESRI公司定义的一个为ArcGIS所用的数据框架,该框架定义了ArcGIS中用到的所有的数据类型.不管ArcGIS的数据存储到何处.以什么格式存储,都脱离不了该框架.也可 ...

  6. ArcGIS中影像与影像，影像与点云之间的配准

    地图配准可分为影像配准和空间配准.影像配准的对象是raster图,譬如TIFF图.配准后的图可以保存为ESRI GRID, TIFF,或ERDAS IMAGINE格式.空间配准(Spatial Adj ...

  7. PIE SDK波段合成

    1.算法功能简介 波段合成功能主要用于将多幅图像合并为一个新的多波段图像(即波段的叠加打包,构建一个新的多波段文件),从而可根据不同的用途选择不同波长范围内的波段合成 RGB 彩色图像. PIE支持算 ...

  8. 介绍ArcGIS中各种数据的打开方法——mxd（地图文档）

    1.加载地图文档 在ArcGIS中,以mxd作为扩展名的文件叫地图文档. 地图文档中只是包含图层的引用,即存储当前地图的图层路径.符号.状态.修饰等信息,并不存储真实的数据层. ArcGIS Map中 ...

  9. arcgis中nodata设为0及其小技巧

    一.arcgis中nodata设为0 两个栅格进行叠加,有时会有一部分没有数据,即用identify点击该区域,Value为NoDat a,而不是像其他非空区域一样有值. 此时注意nodata区域要赋 ...

随机推荐

  1. Ubuntu gnome 16.04下的一些个人配置

    虽说并没有改什么,但还是花了我很长时间去搞明白…… 最开始要看下这里,调下比如系统时间等东西 UPD:安装时千万不要对主目录进行加密 1.登录前调整一下触控板和打开小键盘 先打开/etc/gdm3/I ...

  2. 【BZOJ2227】【ZJOI2011】看电影 [组合数][质因数分解]

    看电影 Time Limit: 10 Sec  Memory Limit: 259 MB[Submit][Status][Discuss] Description 到了难得的假期,小白班上组织大家去看 ...

  3. 【BZOJ2527】【POI2011】Meteors [整体二分]

    Meteors Time Limit: 60 Sec  Memory Limit: 128 MB[Submit][Status][Discuss] Description 这个星球经常会下陨石雨.BI ...

  4. Educational Codeforces Round 40 A B C D E G

    A. Diagonal Walking 题意 将一个序列中所有的\('RU'\)或者\('UR'\)替换成\('D'\),问最终得到的序列最短长度为多少. 思路 贪心 Code #include &l ...

  5. HDU2819（二分图匹配，记录过程）

    Swap Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)Total Submis ...

  6. glib windows下编译

    记录的比较粗糙,但是绝对可行的 一些小的瑕疵以后再解决吧 (android版本的过几天再贴,移植到android已经通过) msys+mingw包下载: http://sourceforge.net/ ...

  7. locust===官方说明文档，关于tasks

    安装: >>> pip  install locust locust在官方simple_code中如下: from locust import HttpLocust, TaskSet ...

  8. phython正则表达式 Python Re模块

    反斜杠问题 与大多数编程语言相同,正则表达式里使用”\”作为转义字符,这就可能造成反斜杠困扰.假如你需要匹配文本中的字符”\”, Python里的原生字符串很好地解决了这个问题,这个例子中的正则表达式 ...

  9. HDU 6373.Pinball -简单的计算几何+物理受力分析 (2018 Multi-University Training Contest 6 1012)

    6373.Pinball 物理受力分析题目. 画的有点丑,通过受力分析,先求出θ角,为arctan(b/a),就是atan(b/a),然后将重力加速度分解为垂直斜面的和平行斜面的,垂直斜面的记为a1, ...

  10. Codeforces 651 C. Watchmen-曼哈顿距离和欧几里得距离

    C. Watchmen   time limit per test 3 seconds memory limit per test 256 megabytes input standard input ...