数据结构6——DFS

一、相关定义

深度优先遍历，也有称为深度优先搜索，简称DFS。其实，就像是一棵树的前序遍历。

初始条件：图G所有顶点均未被访问过，任选一点v。

思想：是从一个顶点V₁开始，沿着一条路一直走到底，如果发现不能到达目标解，那就返回到上一个节点，然后从另一条路开始走到底，这种尽量往深处走的概念即是深度优先的概念。

遍历过程：它从图中某个结点v出发，访问此顶点，然后依次从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中的所有顶点都被访问到为止。

【DFS适合此类题目】

• 给定初始状态跟目标状态，要求判断从初始状态到目标状态是否有解。

二、算法过程

以如下图的无向图G4为例，进行图的深度优先搜索：

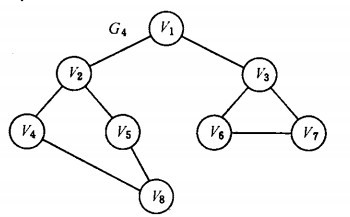
假设从顶点v₁出发进行搜索，在访问了顶点v₁之后，选择邻接点v₂。因为v₂未曾访问，则从v₂出发进行搜索。依次类推，接着从v₄ 、v₈ 、v₅出发进行搜索。在访问了v₅之后，由于v₅的邻接点都已被访问，则搜索回到v₈。由于同样的理由，搜索继续回到v₄，v₂直至v₁，此时由于v₁的另一个邻接点未被访问，则搜索又从v₁到v₃，再继续进行下去由此，得到的顶点访问序列为：

显然，这是一个递归的过程。为了在遍历过程中便于区分顶点是否已被访问，需附设访问标志数组vis[0…n-1], ，其初值为false，一旦某个顶点被访问，则其相应的分量置为true。

三、代码实现

我们用邻接矩阵的方式，则代码如下所示。

/*    图的DFS遍历    */
//邻接矩阵形式实现
//顶点从1开始
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn = 105;        //最大顶点数
typedef int VertexType;     //顶点类型
bool vis[maxn];  

struct Graph{               //邻接矩阵表示的图结构
    VertexType vex[maxn];   //存储顶点
    int arc[maxn][maxn];    //邻接矩阵
    int vexnum,arcnum;      //图的当前顶点数和弧数
};

void createGraph(Graph &g)  //构建无向图
{
    cout<<"请输入顶点数和边数：";
    cin>>g.vexnum>>g.arcnum;

    //构造顶点向量
    cout<<"请依次输入各顶点：\n";
    for(int i=1;i<=g.vexnum;i++){
        scanf("%d",&g.vex[i]);
    }

    //初始化邻接矩阵
    for(int i=1;i<=g.vexnum;i++){
        for(int j=1;j<=g.vexnum;j++){
            g.arc[i][j] = 0;
        }
    }

    //构造邻接矩阵
    VertexType u,v;     //分别是一条弧的弧尾(起点)和弧头(终点)
    printf("每一行输入一条弧依附的顶点（空格分开）：\n");
    for(int i=1;i<=g.arcnum;i++){
        cin>>u>>v;
        g.arc[u][v] = g.arc[v][u] = 1;
    }
}

//邻接矩阵的深度优先递归算法
void DFS(Graph g,int i)
{
    vis[i] = true;
    printf("%d\t",g.vex[i]);                //打印顶点
    for(int j=1;j<=g.vexnum;j++){            //遍历每个顶点
        if(g.arc[i][j]==1 && !vis[j]){        //如果顶点j是顶点i的未访问的邻接点
            DFS(g,j);                        //深度优先搜索顶点j
        }
    }
}

//邻接矩阵的深度遍历操作
void DFSTraverse(Graph g)
{
    for(int i=1;i<=g.vexnum;i++){
        vis[i] = false;                        //初始化所有顶点状态都是未访问过状态
    }
    for(int i=1;i<=g.vexnum;i++){
        if(!vis[i]){
            DFS(g,i);                        //对未访问的顶点调用DFS，若是连通图，只会执行一次
        }
    }
}

int main()
{
    Graph g;
    createGraph(g);
    DFSTraverse(g);
    return 0;
}

如果使用的是邻接表存储结构，其DFSTraverse函数的代码几乎是相同的，只是在递归函数中因为将数组换成了链表而有不同，代码如下。

//邻接表的深度递归算法
void DFS(GraphList g, int i)
{
    EdgeNode *p;
    vis[i] = true;
    printf("%d ", g->adjList[i].data);   //打印顶点，也可以其他操作
    p = g->adjList[i].firstedge;
    while(p)
    {
        if(!vis[p->adjvex])
        {
            DFS(g, p->adjvex);           //对访问的邻接顶点递归调用
        }
        p = p->next;
    }
}

//邻接表的深度遍历操作
void DFSTraverse(GraphList g)
{
    int i;
    for(i = 0; i < g.numVertexes; i++)
    {
        vis[i] = false;
    }
    for(i = 0; i < g.numVertexes; i++)
    {
        if(!vis[i])
        {
            DFS(g, i);
        }
    }
}

分析上述算法，在遍历时，对图中每个顶点至多调用一次DFS 函数，因为一旦某个顶点被标志成已被访问，就不再从它出发进行搜索。因此，遍历图的过程实质上是对每个顶点查找其邻接点的过程。其耗费的时间则取决于所采用的存储结构。

当用二维数组表示邻接矩阵图的存储结构时，查找每个顶点的邻接点所需时间为O(n²) ，其中n为图中顶点数。

而当以邻接表作图的存储结构时，找邻接点所需时间为O(e)，其中e 为无向图中边的数或有向图中弧的数。由此，当以邻接表作存储结构时，深度优先搜索遍历图的时间复杂度为O(n+e) 。　　

对比两个不同的存储结构的深度优先遍历算法，显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。

四、沙场练兵

题目一、滑雪

题目二、棋盘问题

DFS做题小结

五、知识扩展

不知道你注意到没，在深度/广度搜索的过程中，其实相邻节点的加入如果是有一定策略的话，对算法的效率是有很大影响的，你可以做一下简单马周游跟马周游这两个题，你就有所体会，你会发现你在搜索的过程中，用一定策略去访问相邻节点会提升很大的效率。 这些运用到的贪心的思想，你可以再看看启发式搜索的算法，例如A*算法等。