编写一个computer类，类中含有一个求n的阶乘的方法，将该类打包，

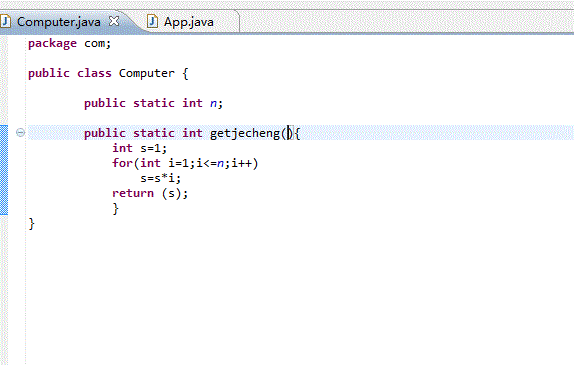
在另一个包中引入包，在主类中定义computer类的对象，调用求n的阶乘的方法，并输出结果

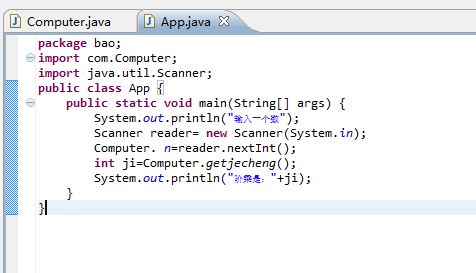
结果

求n的阶乘！的更多相关文章

  1. 汇编语言-求X的阶乘

    1. 题目:求X的阶乘值 2. 要求:输入一个整型数(不超过10),求出其阶乘值后输出,求阶乘的算法用子程序来实现. 3. 提示:可以用递归来实现,也可以用简单的循环来实现. 这里使用循环来实现: 对 ...

  2. C语言－求1-20的阶乘的和（函数的递归）

    // //  main.c //  C语言 // //  Created by wanghy on 15/9/5. //  Copyright (c) 2015年 wanghy. All rights ...

  3. 递归和非递归分别实现求n的阶乘

    思路:举例求6的阶乘,6*5*4*3*2*1.可以将5开始看成另一个整型变量n,用一个循环每次将n的值减少1,.而递归也是如此,每次调用函数的时候将变量减一就可以. 方法一:非递归 //非递归: #i ...

  4. 求N的阶乘N!中末尾0的个数

    求N的阶乘N!中末尾0的个数 有道问题是这样的:给定一个正整数N,那么N的阶乘N!末尾中有多少个0呢?例如:N=10,N=3628800,则N!的末尾有两个0:直接上干货,算法思想如下:对于任意一个正 ...

  5. 大数问题：求n的阶乘

    题目:求100! 这看起来是一个非常简答的问题,递归解之毫无压力 int func(int n){ if(n <= 1) return 1; else return n*func(n-1); } ...

  6. 2717: 递归函数求n的阶乘

    2717: 递归函数求n的阶乘 Time Limit: 1 Sec  Memory Limit: 128 MBSubmit: 1329  Solved: 942[Submit][Status][Web ...

  7. 题目一：编写一个类Computer，类中含有一个求n的阶乘的方法

    作业:编写一个类Computer,类中含有一个求n的阶乘的方法.将该类打包,并在另一包中的Java文件App.java中引入包,在主类中定义Computer类的对象,调用求n的阶乘的方法(n值由参数决 ...

  8. POJ 1401：Factorial 求一个数阶乘的末尾0的个数

    Factorial Time Limit: 1500MS   Memory Limit: 65536K Total Submissions: 15137   Accepted: 9349 Descri ...

  9. C语言求n的阶乘（n!）

    从键盘输入一个数,求出这个数的阶乘,即 n!. 算法思想 首先要清楚阶乘定义,所谓 n 的阶乘,就是从 1 开始乘以比前一个数大 1 的数,一直乘到 n,用公式表示就是:1×2×3×4×…×(n-2) ...

随机推荐

  1. WebShell代码分析溯源(四)

    WebShell代码分析溯源(四) 一.一句话变形马样本 <?php @$_++;$__=("`"^"?").(":"^"} ...

  2. Vultr主机绑定域名

    1.在腾讯云上注册域名 然后,域名实名认证 2.Vultr主机购买(看我之前写的:手把手教你如何自己搭梯子) 然后会获取到一个服务器IP地址 3.绑定域名与IP 点解,解析后会弹出让你输入IP地址,此 ...

  3. GitLab-使用SSH的方式拉取和推送项目

    场景 Docker Compose部署GitLab服务,搭建自己的代码托管平台(图文教程): https://blog.csdn.net/BADAO_LIUMANG_QIZHI/article/det ...

  4. delphi使用Chilkat 组件和库从SFTP下载文件

    官网地址:https://www.example-code.com/delphiDll/default.asp 实例代码:(不包括全局解锁)  密码生成器:https://www.cnblogs.co ...

  5. koa2使用es7 的装饰器decorator

    本文主要讲述我在做项目中使用装饰器(decorator)来动态加载koa-router的路由的一个基础架构. 目前JavaScript 对decorator 是不支持,但是可以用babel 来编译 既 ...

  6. JS---DOM---设置和获取---标签内容和文本内容

    设置和获取---标签内容和文本内容   总结---设置: 使用innerText主要是设置文本的, 设置标签内容, 是没有标签的效果的 innerHTML是可以设置文本内容 innerHTML主要的作 ...

  7. java基础学习笔记 第二周(面向对象)

    Day01 什么是抽象数据类型:将不同数据类型的集合组成的一个整体,我们称为抽象数据类型 类就是一个抽象数据类型 成员变量:类中的数据类型就是成员变量(属性) 方法:类中的一些行为就是方法 面向过程( ...

  8. python 基础学习笔记（7）--迭送器

    **函数名的运用** - [ ] 函数名是一个变量, 但它是一个特殊的变量, 与括号配合可以执行函数的变量 **函数名的内存地址** ```  def func():  print('666')  p ...

  9. 编辑器之神vim的一些常用快捷键整理

    yy:复制 光标所在的这一行 4yy:复制 光标所在行开始向下的4行 p:粘贴 dd:剪切(删除) 光标所在的这一行 4dd:剪切(删除) 光标所在行向下的4行 D:从当前的光标开始向后剪切,一直到行 ...

  10. JS数组去掉某一个元素

    /**数组去掉某一个元素**/ Array.prototype.remove = function(val) { var index = this.indexOf(val); if (index &g ...