最小生成树与最短路径--C语言实现

接昨天，在这里给出图的其中一种应用：最小生成树算法（Prime算法和Kruskal算法）。两种算法的区别就是：Prime算法以顶点为主线，适合用于顶点少，边密集的图结构；Kruskal算法以边为主线，适合于顶点比较多，但是边比较稀疏的图结构。代码如下，亲测，可执行，在最后也给出输入数据的形式。

 /*
 图结构的最小生成树算法：
     1.prime算法：按顶点查找，遍历当前顶点所有邻接边，选择权值最小值，
     记录这两个顶点，直到所有的顶点都已处理

     2.Kruskal算法：按边查找，将所有边的权值排序，以此选择权值最小的边，
     检查该边连接的两个顶点是否状态一致（都已处理，或都未处理），
     直到所有顶点都标记为处理过
 */

 #include<stdio.h>
 #define INFINITY 65535
 #define MAXVEX 100

 //边集数组图结构
 typedef struct                        //边结构体
 {
     int start;
     int end;
     int weight;
 }Edges;

 typedef struct                        //图结构
 {
     char Vex[MAXVEX];                //顶点数组
     Edges edge[MAXVEX];                //边数组
     int numVexes;                    //顶点数量
     int numEdges;                    //边数量
 }E_VGraph;

 //邻接矩阵图结构
 typedef struct
 {
     char Vex[MAXVEX];                //顶点数组
     int arc[MAXVEX][MAXVEX];        //边数组
     int numVexes;                    //顶点数量
     int numEdges;                    //边数量
 }Graph;

 //邻接矩阵图结构转化为边集数组图结构，并将权值升序排序
 void G_EVConversion(Graph G, E_VGraph *G1)
 {
     int i,j,k,lowest;
     Edges edges[MAXVEX];
     G1->numVexes = G.numVexes;                    //将邻接矩阵顶点数赋值于边集数组
     G1->numEdges = G.numEdges;                    //将邻接矩阵边数赋值于边集数组
     for(i = ; i < G.numVexes; i++)                //遍历邻接矩阵中的每个顶点
     {
         for(j = i+; j < G.numVexes; j++)        //遍历除当前结点之后的结点
         {
             if(G.arc[i][j] != INFINITY)            //判断两顶点之间是否有边
             {
                 edges[i].start = i;            //记录当前边的起点
                 edges[i].end = j;            //记录当前边的终点
                 edges[i].weight = G.arc[i][j];    //记录当前边的权重
                 printf("%d       %d\n",G.arc[i][j],edges[i].weight);
             }
         }
     }
     printf("\n\n");
     for(i = ; i < G.numEdges; i++)            //选择排序edges数组
     {
         lowest = INFINITY;
         for(j = ; j < G.numEdges; j++)
         {
             printf("%d     %d       %d\n",j,edges[j].weight,lowest);
             if(edges[j].weight <= lowest)
             {
                 lowest = edges[j].weight;
                 k = j;
                 printf("\n%d\n",k);
             }
         }
         G1->edge[i].start = edges[k].start;        //将每轮找出的最小权值的边的信息
         G1->edge[i].end = edges[k].end;            //写入边集数组中
         G1->edge[i].weight = edges[k].weight;
         edges[k].weight = INFINITY;                //赋值完毕，将此最小权值设为最大值
         printf("\n");
         printf("%d\n",G1->edge[i].weight);
     }
 }

 //确认函数
 int Find(int *parent, int f)
 {
     if(parent[f] > )            //检查此顶点是否处理过，若大于0，则处理过
         f = parent[f];            //将parent[f]的值赋值给f
     return f;                    //返回f
 }

 //克鲁斯卡尔算法构造最小生成树
 void minTreeKruskal(E_VGraph G1)
 {
     int i,j,k,w,n,m;
     int parent[MAXVEX];                    //记录结点状态
     int lowest = ;                            //最小权值
     for(i = ; i < G1.numVexes; i++)    //初始化记录数组，所有顶点记为未被处理
         parent[i] = ;
     for(i = ; i < G1.numEdges; i++)    //遍历边集数组
     {
         n = Find(parent, G1.edge[i].start);    //得到当前边的开始顶点的状态
         m = Find(parent, G1.edge[i].end);        //得到当前边的结束顶点的状态
         if(n != m)                                //若状态不同（即，起点与终点一个处理过，一个未处理）
         {
             lowest += G1.edge[i].weight;        //将此边的权值加入最小生成树权值
             parent[G1.edge[i].start] = ;        //将起点记为处理过
             parent[G1.edge[i].end] = ;            //将终点记为处理过
         }
     }
     printf("克鲁斯卡尔算法构建最小生成树的权值为：%d\n", lowest);
 }

 void CreatGraph(Graph *G)            //创建图结构
 {
     int i,j,k,w,a[];
     printf("请输入顶点与边的数量：");
     scanf("%d,%d",&G->numVexes,&G->numEdges);        //写入顶点数量与边的数量
     for(i = ; i < G->numVexes; i++)                //初始化顶点数组
     {
         printf("请输入第%d个顶点：", i);
         scanf("%c",&G->Vex[i]);
         getchar();
     }
     for(i = ; i < G->numVexes; i++)                //初始化边数组
         for(j = ; j < G->numVexes; j++)
             G->arc[i][j] = INFINITY;

     for(k = ; k < G->numEdges; k++)                //构造边的数组
     {
         printf("请输入边的起点与终点的下标及其权重：");
         scanf("%d,%d,%d",&i,&j,&w);
         G->arc[i][j] = G->arc[j][i] = w;            //无向图的对称性
     }
     printf("创建成功\n");
 }

 //Prim算法构造最小生成树
 void minTreePrim(Graph G,int i)
 {
     int j,k,l,w,count,zongWeight;
     int visited[MAXVEX];                //记录访问过的顶点
     int lowest[MAXVEX];                    //记录最小权值
     for(j = ; j < G.numVexes; j++)        //初始化访问数组，将所有顶点记为未访问过
         visited[j] = ;
     visited[i] = ;                        //将传入顶点记为访问过
     lowest[i] = ;                        //将此顶点的权值记为0
     zongWeight = ;                        //总权重为0
     count = ;                            //访问过的顶点数量为1
     int wei = INFINITY;                    //权重变量记为最大值
     while(count < G.numVexes)            //只要访问过的顶点数目小于图中顶点数目，继续循环
     {
         for(k = ; k < G.numVexes; k++)    //遍历访问过的顶点数组
         {
             if(visited[k] == )            //如果当前顶点访问了，寻找它的邻接边
             {
                 for(l = ; l < G.numVexes; l++)        //遍历图中所有顶点
                 {
                     if(visited[l] ==  && G.arc[k][l] < wei)    //如果未被访问，且权值小于权值变量
                     {
                         wei = G.arc[k][l];            //更新权值变量
                         w = l;                        //更新最小顶点
                     }
                 }
             }
         }
         visited[w] = ;                    //将最小权值顶点记为访问过
         lowest[l] = wei;                //记录他的权值
         zongWeight += wei;                //加入总权重
         count++;                        //访问过的顶点数量+1
         wei = INFINITY;

     }
     printf("最小生成树的权值为：%d\n",zongWeight);
 }

 void main()
 {
     Graph G;
     E_VGraph G1;

     printf("请构造图结构：\n");
     CreatGraph(&G);

     printf("\n\n");
     printf("普利姆算法构建最小生成树\n");
     minTreePrim(G,);

     printf("\n\n");
     printf("克鲁斯卡尔算法构建最小生成树\n");
     G_EVConversion(G, &G1);
     minTreeKruskal(G1);
 }

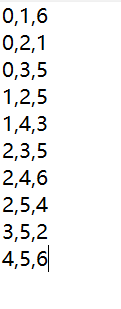
本来今天应该将最小生成树与最短路径的算法一起上传，但是我写的最短路径算法还有一些bug没调好，所以要延迟一天，勿怪。