【Offer】[36] 【二叉搜索树与双向链表】

• 题目描述
• 思路分析
• 测试用例
• Java代码
• 代码链接

题目描述

　　输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。比如，输入下图中左边的二叉搜索树，则输出转换之后的排序双向链表。
　　


　

牛客网刷题地址

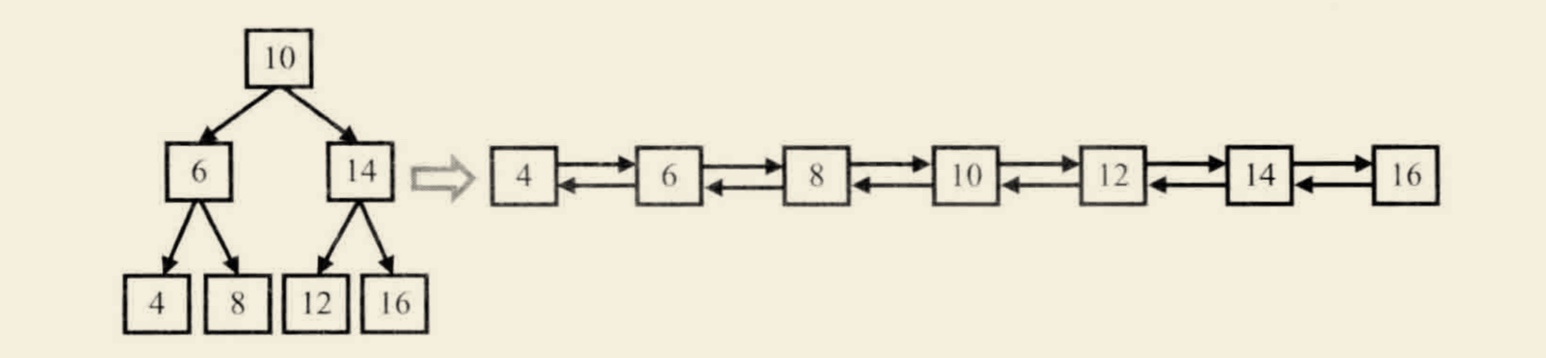
思路分析

　　利用中序遍历的思想，当我们遍历到根节点时，它的左子树已经转换成一个排序的链表了，并且处在链表中的最后一个节点是当前值最大的一个节点，将这个节点和根节点连接起来，此时链表的最后一个节点就是根节点，接着遍历右子树，并将根节点与右子树中最小的节点连接起来。

测试用例

1. 功能测试：输入的二叉树是完全二叉树;所有节点都没有左/右子树的二叉树;只有一个节点的二叉树。
2. 特殊输入测试：指向二叉树根节点的指针为nullptr指针。

Java代码

public class Offer36 {
    public static void main(String[] args) {
        test1();
        test2();
        test3();

    }

    public static TreeNode Convert(TreeNode pRootOfTree) {
        return Solution1(pRootOfTree);
    }

    private static TreeNode Solution1(TreeNode pRootOfTree) {
        if (pRootOfTree == null) {
            return pRootOfTree;
        }
        TreeNode lastNodeInList = null;
        lastNodeInList = covertCore(pRootOfTree, lastNodeInList);
        TreeNode firstNodeInList = lastNodeInList;
        while (firstNodeInList != null && firstNodeInList.left != null) {
            firstNodeInList = firstNodeInList.left;
        }
        return firstNodeInList;
    }

    private static TreeNode covertCore(TreeNode pRootOfTree, TreeNode lastNodeInList) {
        if (pRootOfTree.left != null) {
            lastNodeInList = covertCore(pRootOfTree.left, lastNodeInList);
        }
        pRootOfTree.left = lastNodeInList;
        if (lastNodeInList != null) {
            lastNodeInList.right = pRootOfTree;
        }

        lastNodeInList = pRootOfTree;
        if (pRootOfTree.right != null) {
            lastNodeInList = covertCore(pRootOfTree.right, lastNodeInList);
        }

        return lastNodeInList;
    }

    private static void test1() {

    }

    private static void test2() {

    }

    private static void test3() {

    }
}

代码链接

剑指Offer代码-Java