相机位姿求解——P3P问题

　　1、位姿求解是计算机视觉中经常遇到的，Perspective-n-Points, PnP(P3P)提供了一种解决方案，它是一种由3D-2D的位姿求解方式，即需要已知匹配的3D点和图像2D点。目前遇到的场景主要有两个，其一是求解相机相对于某2维图像/3维物体的位姿，具体的如AR应用，人脸跟踪等；其二就是SLAM算法中估计相机位姿时通常需要PnP给出相机初始位姿。

　　这里要说明的是在场景1中，我们通常输入的是物体在世界坐标系下的3D点以及这些3D点在图像上投影的2D点，因此求得的是相机（相机坐标系）相对于真实物体（世界坐标系）的位姿，如图所示：

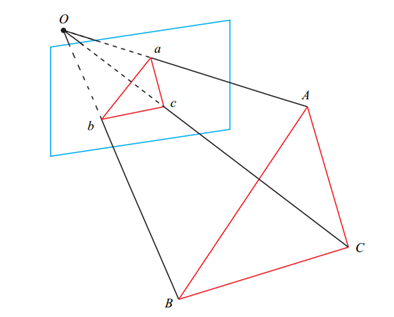
而在场景2中，通常输入的是上一帧中的3D点（在上一帧的相机坐标系下表示的点）和这些3D点在当前帧中的投影得到的2D点，所以它求得的是当前帧相对于上一帧的位姿变换，如图所示：

两种情况本质上是相同的，都是基于已知3D点和对应的图像2D点求解相机运动的过程。下面详细探讨P3P的求解过程。

　　2、我们首先需要知道的是P3P并不是直接根据3D-2D点求出相机位姿矩阵，而是先求出对应的2D点在当前相机坐标系下的3D坐标，然后根据世界坐标系下的3D坐标和当前相机坐标系下的3D坐标求解相机位姿的。P3P的求解是从余弦定理开始的，设相机坐标中心为点P，A、B、C为不共线的三个3D点，D为验证3D点，根据余弦定理有如下公式：

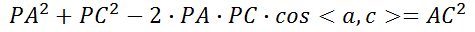
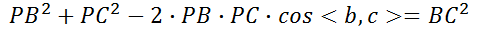
接下来其实是对上述3个式子消元化简的过程，同时除以

，

并且使得

，

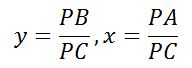则可得：

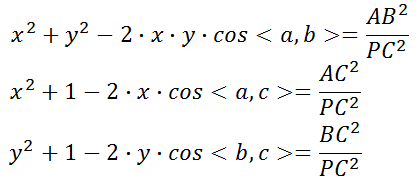
然后再次进行替换，另：

，

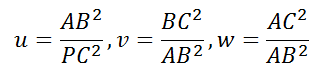可得：

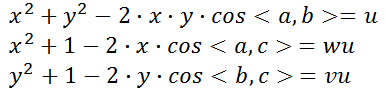
将第一个式子代入第2，3式，可以化简得到：

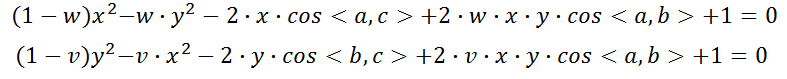
接下来的过程就是如何通过上述两个式子求解A，B，C在当前相机坐标系下的坐标。首先需要明确的是哪些量是已知量，输入的是3D-2D的坐标，也即

都是已知的。因为首先AB，BC，AC的距离都是可以根据输入的3D点求得，而输入的2D点可以求解三个余弦值（如何求解，像素坐标根据相机内参矩阵和畸变参数可以求得在归一化图像平面上的3D坐标，此时 z=1，故余弦值可求）。此时未知数仅x，y两个，所以理论上两个未知数两个方程，是可求的。（从x，y求PA，PB，PC也可求）

　　3、具体的求解过程：

　　3.1、首先是根据2D坐标求解余弦值得过程，首先是由像素坐标到归一化图像坐标的转变，根据就是相机模型

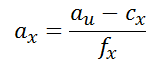
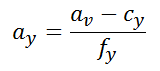
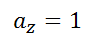
然后是L2归一化的过程，我们知道求解角度的时候用的是归一化坐标（此归一化非彼归一化，上面是归一化到z值等于1的平面上，这里讲的是数学上的归一化）

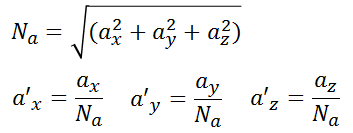
有了上述值就可以求解余弦值了

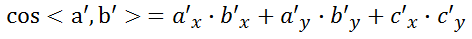
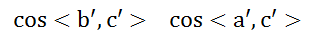同理可求。

　　3.2、根据3D坐标求解AB，AC，BC的值，以AB为例

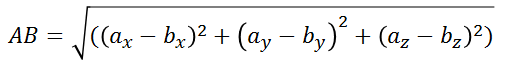
AC，BC同理可求，所以v，w也可以求解。

　　3.3、接下来就是一个二元二次方程的求解，比较难求，但是这在数学上是可以求解的，需要用到Wu Ritt的零点分解方法，它可以将原方程等效成一组特征列（Characteristic Serial, CS），凡是原方程组的解都会是CS的解，但是CS的解不一定是原方程的解，所以需要验证，这里的等效方程为：

其中的未知数a1~a4都是已知的，因为原方程的系数是已知的，后文有系数附录，因此我们可以求得x，y的值，4次方程组理论上有4组解，但其实只有一组是合适的。

　　3.4、求得了x，y的值，就可以求取PA，PB，PC的值，根据下面的公式，AB已知，可以先求PC，然后分别求解PB，PA：

但是我们需要的是A，B，C在相机坐标系下的坐标，而不是PA，PB，PC的长度，所以还需根据长度求取点的坐标，求解方法是用向量公式：

其中a是单位向量，||PA||是模值，所得即A在相机坐标系下的坐标。

　　最后求得了A，B，C的坐标就可以通过世界坐标系到当前相机坐标的变换求解相机位姿，注意上面求得了4组解，这里需要使用D点确认哪组解是最合适的。

　　4、代码对应：看看上述过程是如何代码实现的

    //像素坐标转变为归一化图像坐标；
    mu0 = inv_fx * mu0 - cx_fx;
    mv0 = inv_fy * mv0 - cy_fy;
    //归一化图像坐标归一化
    norm = sqrt(mu0 * mu0 + mv0 * mv0 + );
    mk0 = . / norm; mu0 *= mk0; mv0 *= mk0;
 
    mu1 = inv_fx * mu1 - cx_fx;
    mv1 = inv_fy * mv1 - cy_fy;
    norm = sqrt(mu1 * mu1 + mv1 * mv1 + );
    mk1 = . / norm; mu1 *= mk1; mv1 *= mk1;
 
    mu2 = inv_fx * mu2 - cx_fx;
    mv2 = inv_fy * mv2 - cy_fy;
    norm = sqrt(mu2 * mu2 + mv2 * mv2 + );
    mk2 = . / norm; mu2 *= mk2; mv2 *= mk2;
 
    //世界坐标系中，ABC三点的距离；
    double distances[];
    distances[] = sqrt( (X1 - X2) * (X1 - X2) + (Y1 - Y2) * (Y1 - Y2) + (Z1 - Z2) * (Z1 - Z2) );
    distances[] = sqrt( (X0 - X2) * (X0 - X2) + (Y0 - Y2) * (Y0 - Y2) + (Z0 - Z2) * (Z0 - Z2) );
    distances[] = sqrt( (X0 - X1) * (X0 - X1) + (Y0 - Y1) * (Y0 - Y1) + (Z0 - Z1) * (Z0 - Z1) );
 
    //三点之间的角度值；
    // Calculate angles
    double cosines[];
    cosines[] = mu1 * mu2 + mv1 * mv2 + mk1 * mk2;
    cosines[] = mu0 * mu2 + mv0 * mv2 + mk0 * mk2;
    cosines[] = mu0 * mu1 + mv0 * mv1 + mk0 * mk1;
 
    //吴消元法求解PA，PB，PC的值，有四组解；
    double lengths[][];
    int n = solve_for_lengths(lengths, distances, cosines);
 
    int nb_solutions = ;
    for(int i = ; i < n; i++) {
        double M_orig[][];
 
        //对每个点求坐标值，单位向量乘以距离；
        M_orig[][] = lengths[i][] * mu0;
        M_orig[][] = lengths[i][] * mv0;
        M_orig[][] = lengths[i][] * mk0;
 
        M_orig[][] = lengths[i][] * mu1;
        M_orig[][] = lengths[i][] * mv1;
        M_orig[][] = lengths[i][] * mk1;
 
        M_orig[][] = lengths[i][] * mu2;
        M_orig[][] = lengths[i][] * mv2;
        M_orig[][] = lengths[i][] * mk2;
 
        //计算每个解对应的位姿矩阵R，t
        if (!align(M_orig, X0, Y0, Z0, X1, Y1, Z1, X2, Y2, Z2, R[nb_solutions], t[nb_solutions]))
            continue;
 
        nb_solutions++;
    }

　　这里面主要是使用吴消元法求解PA，PB，PC的距离

/// Given 3D distances between three points and cosines of 3 angles at the apex, calculates

/// the lentghs of the line segments connecting projection center (P) and the three 3D points (A, B, C).

/// Returned distances are for |PA|, |PB|, |PC| respectively.

/// Only the solution to the main branch.

/// Reference : X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang; "Complete Solution Classification for the Perspective-Three-Point Problem"

/// IEEE Trans. on PAMI, vol. 25, No. 8, August 2003

/// \param lengths3D Lengths of line segments up to four solutions.

/// \param dist3D Distance between 3D points in pairs |BC|, |AC|, |AB|.

/// \param cosines Cosine of the angles /_BPC, /_APC, /_APB.

/// \returns Number of solutions.

/// WARNING: NOT ALL THE DEGENERATE CASES ARE IMPLEMENTED

int p3p::solve_for_lengths(double lengths[][], double distances[], double cosines[])
{
    //吴消元法，数据准备
    double p = cosines[] * ;
    double q = cosines[] * ;
    double r = cosines[] * ;
 
    double inv_d22 = . / (distances[] * distances[]);
    double a = inv_d22 * (distances[] * distances[]);
    double b = inv_d22 * (distances[] * distances[]);
 
    double a2 = a * a, b2 = b * b, p2 = p * p, q2 = q * q, r2 = r * r;
    double pr = p * r, pqr = q * pr;
 
    // Check reality condition (the four points should not be coplanar)
    if (p2 + q2 + r2 - pqr -  == )
        return ;
 
    double ab = a * b, a_2 = *a;
 
    double A = - * b + b2 + a2 +  + ab*( - r2) - a_2;
 
    //A, B, C, D, E 为四次多项式的系数；
    // Check reality condition
    if (A == ) return ;
 
    double a_4 = *a;
 
    double B = q*(-*(ab + a2 +  - b) + r2*ab + a_4) + pr*(b - b2 + ab);
    double C = q2 + b2*(r2 + p2 - ) - b*(p2 + pqr) - ab*(r2 + pqr) + (a2 - a_2)*( + q2) + ;
    double D = pr*(ab-b2+b) + q*((p2-)*b +  * (ab - a2) + a_4 - );
    double E =  + *(b - a - ab) + b2 - b*p2 + a2;
 
    double temp = (p2*(a-+b) + r2*(a--b) + pqr - a*pqr);
    double b0 = b * temp * temp;
    // Check reality condition
    if (b0 == )
        return ;
 
    //求解四次多项式；
    double real_roots[];
    int n = solve_deg4(A, B, C, D, E,  real_roots[], real_roots[], real_roots[], real_roots[]);
 
    if (n == )
        return ;
 
    int nb_solutions = ;
    double r3 = r2*r, pr2 = p*r2, r3q = r3 * q;
    double inv_b0 = . / b0;
 
    // For each solution of x
    for(int i = ; i < n; i++) {
        double x = real_roots[i];
 
        // Check reality condition
        if (x <= )
            continue;
 
        double x2 = x*x;
　　　　//对应附录中的b1
        double b1 =
            ((-a-b)*x2 + (q*a-q)*x +  - a + b) *
            (((r3*(a2 + ab*( - r2) - a_2 + b2 - *b + )) * x +
 
            (r3q*(*(b-a2) + a_4 + ab*(r2 - ) - ) + pr2*( + a2 + *(ab-a-b) + r2*(b - b2) + b2))) * x2 +
 
            (r3*(q2*(-*a+a2) + r2*(b2-ab) - a_4 + *(a2 - b2) + ) + r*p2*(b2 + *(ab - b - a) +  + a2) + pr2*q*(a_4 + *(b - ab - a2) -  - r2*b)) * x +
 
            *r3q*(a_2 - b - a2 + ab - ) + pr2*(q2 - a_4 + *(a2 - b2) + r2*b + q2*(a2 - a_2) + ) +
            p2*(p*(*(ab - a - b) + a2 + b2 + ) + *q*r*(b + a_2 - a2 - ab - )));
 
        // Check reality condition
        if (b1 <= )
            continue;
 
        double y = inv_b0 * b1;
        double v = x2 + y*y - x*y*r;
 
        if (v <= )
            continue;
 
        double Z = distances[] / sqrt(v);
        double X = x * Z;
        double Y = y * Z;
 
        lengths[nb_solutions][] = X;
        lengths[nb_solutions][] = Y;
        lengths[nb_solutions][] = Z;
 
        nb_solutions++;
    }
 
    return nb_solutions;
}

　　看看是如何从4组解中选择合适的解的：

    int ns = ;
    double min_reproj = ;
    for(int i = ; i < n; i++) {
        double X3p = Rs[i][][] * X3 + Rs[i][][] * Y3 + Rs[i][][] * Z3 + ts[i][];
        double Y3p = Rs[i][][] * X3 + Rs[i][][] * Y3 + Rs[i][][] * Z3 + ts[i][];
        double Z3p = Rs[i][][] * X3 + Rs[i][][] * Y3 + Rs[i][][] * Z3 + ts[i][];
        double mu3p = cx + fx * X3p / Z3p;
        double mv3p = cy + fy * Y3p / Z3p;
        //通过R，t计算第4个点的重投影误差选择合理的解
        double reproj = (mu3p - mu3) * (mu3p - mu3) + (mv3p - mv3) * (mv3p - mv3);
        //选择重投影误差最小的解
        if (i ==  || min_reproj > reproj) {
            ns = i;
            min_reproj = reproj;
        }
    }

大概就酱。

附：吴消元法求解系数

，，

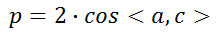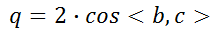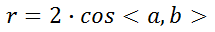
参考：http://iplimage.com/blog/p3p-perspective-point-overview/#Appendix