FZU Monthly-201906 tutorial

题目(难度递增)	easy	easy-medium	medium	medium-hard	hard
思维难度	AE	B	DG	CF	H

A. Xorisk

求出前缀异或和。从头到尾扫一遍，维护map[x]表示之前有多少个前缀异或和为x，枚举到第i个数就加上map[ai^k]即可。

B. short-path-problem

裸的最短路，构造数据卡掉了SPFA写法，使用Dijkstra就可以正常AC。

C. cover

可以先把字符串插入AC自动机里，用dp来计数，状态表示为f[i][j][k]，表示长度为i，现在在自动机状态为j，而且已经有长度为k没被覆盖了，转移就是枚举4个字符，转移一下自动机状态和没被覆盖的长度

D. banzhuan

题意

三维空间一块方形空间，要摆一些实心格子，每个格子有个代价，这格子可以摆当且仅当下面是地面或者下面的格子已经摆了，求最大代价最小代价

题解：贪心+数学

这个题目，出题组搞出了个假的贪心策略，也就是说标程写了个假算法，特在此致歉，不知道在考试期间，有没有给选手们带来困扰或者不必要的麻烦，但是大部分选手这题都没有提交，不知道是否是时间安排不当，这个题目定位是个仅次于签到的贪心难度，虽然纠正之后的贪心难度，要比之前的稍微难一些，但是贪心策略是不难想到的，选手们应该要有尝试；经过后来补充测试，本场冠军的这道题在倒数第二发通过了，时间离结束也不远

另一方面，本题题面还有点小歧义，虽然按照正常一些的理解，是符合出题人的设定的，但是没有严格明确强调，主要是中文题面，里面有个字“放”，有点语义上的歧义，比如可以理解为放这个动作，也可以理解为放着这种状态

显然最底下一层要铺满，考虑上面的任意一层，如果你把贡献的$z$这个因子，提取出来，那么容易发现这个一层就转化为一个平面的问题了，因为剩余的因子大家是一样的

考虑一层如何摆布才能最小：

1)考虑最优的方案中，2-n这些列显然不会同一列出现两个；如若不然，设有两个棋子，上面这个设为$A$，下面设为$B$，可以把$A$移动到第一列，这样显然效果更好，且代价更低，故由调整法可证2-n这些列最多一个棋子，且每列至少一个，故每列严格一个棋子

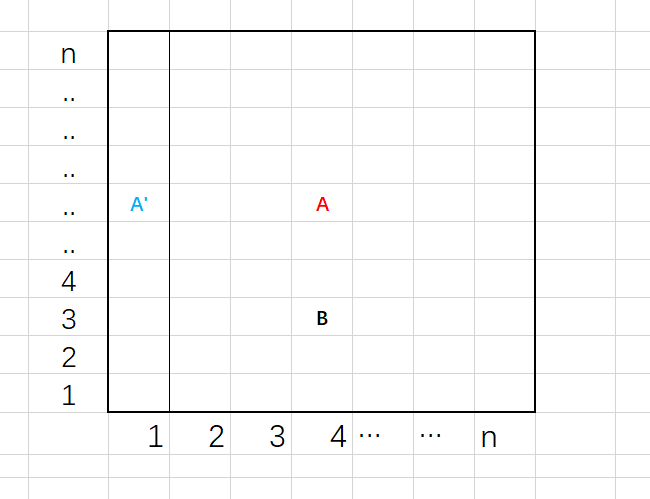
2)2-n每一列的棋子一定放在第1行，反证法，如若不然，将一个棋子$C$拆分为两个棋子$C1$和$C2$，如图：
\[
xy^2-(x1^2+1y^2)=xy^2-x-y^2+1-1=(x-1)(y^2-1)-1 \ge 2 \gt 0,\forall x \ge 2,y \ge2
\]
故由调整法知2-n的棋子严格放在第1行

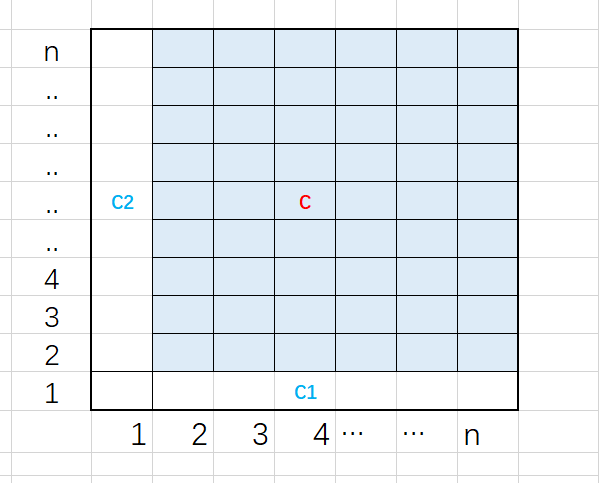
3)2-n行每行只会放一个棋子，且放在第一列，且$(1,1)$不放棋子，显然

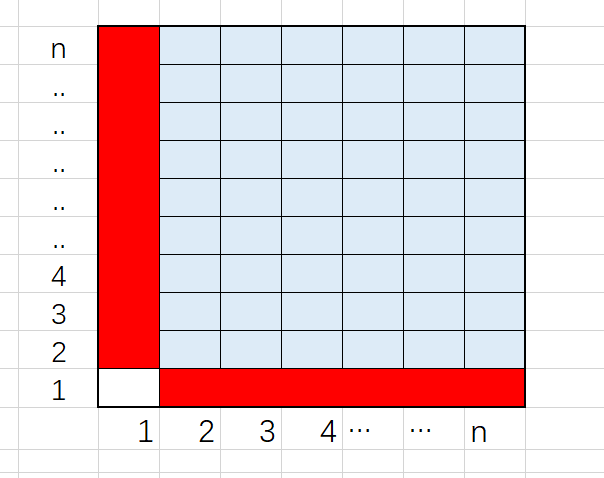
最优排布一层的就是这样，红色部分为棋子

现在考虑很多层，假设前$k$层已经都排布好了，现在放第$k+1$层，因为第$k+1$层这样放是最优的，且恰好可以放在第$k$层上，由归纳法知就这样放满$n$层就是可行且最优的方案

最大值显然就是全部排满$n^3$，只要计算一下答案即可
\[
ret_{max}=(\sum_{z=1}^nz)(\sum_{x=1}^nx)(\sum_{y=1}^ny^2) \\
ret_{min}=(\sum_{x=1}^nx)(\sum_{y=1}^ny^2)+\sum_{z=2}^nz(\sum_{x=2}^nx+\sum_{y=2}^ny^2)
\]

E. spanning-tree

题意

问1到n这些数，构成完全图，w(i,j)=i+j，次小生成树

题解

很简单的贪心，就所有点都连1，这样就是最小的，然后把3连1改成3连2即可，就是次小的了(比最小的多1)

证明：

首先，最小生成树严格有$n-1$条边，$2n-2$个度之和，那么答案显然为$2n-2$的正整数之和$S=\sum_{i=1}^na_i$

最小生成树要联通，即每个点至少一个度，那么其中$n$个数固定为$1,2,3\dots n$

剩下的$n-2$个数，显然至少为$1$，那么$S \ge n-2 +\sum_{i=1}^ni=n(n+1)/2+n-2$

前面我们显然找到了一种构造方案，使得上式取到等号

F. 8862015

数位DP中的基础题

G. Euclid

可以发现两个式子可以拼成一个矩形内整点数量，所以答案是（p - 1） * (q - 1) /4，注意p和q相等时拼的线要多算一次，所以还要加 (p - 1) / 2.

H. i-love-gcd

题意与题解

本题留有空白，给选手们自己思考，考点和算法方向也隐藏