NOIP 2018 简要题解

从这里开始

Day 1

Problem A

　　考虑贪心地选取极大非 0 段减少。

　　如果两次操作有交，并且不是包含关系，那么把其中一次操作的，但另一次没有操作的移过去，然后就变成了上面那个贪心了。

Code

#include <iostream>
#include <cstdlib>
#include <cstdio>
using namespace std;
typedef bool boolean;

const int N = 1e5 + 5;

int n;
int res = 0;
int ar[N];

inline void init() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
		scanf("%d", ar + i);
}

inline void solve() {
	int lst = 0;
	for (int i = 1; i <= n; i++) {
		if (ar[i] > lst)
			res += ar[i] - lst;
		lst = ar[i];
	}
	printf("%d\n", res);
}

int main() {
	freopen("road.in", "r", stdin);
	freopen("road.out", "w", stdout);
	init();
	solve();
	return 0;
}

Problem B

　　考虑从小到达确定 $b$ 中的面额。不难发现：

• $b$ 一定是 $a$ 的子集。
• $a$ 中一种面值不在 $b$ 中当且仅当它能被除掉它之后的面额表示出来。

Code

#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;

const int N = 105, M = 25005;

int T;
int n, m;
int a[N];
bitset<M> f;

void solve() {
	scanf("%d", &n);
	m = 0;
	for (int i = 1; i <= n; i++) {
		scanf("%d", a + i);
		m = max(m, a[i]);
	}
	sort(a + 1, a + n + 1);
	f.reset();
	f.set(0);
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		if (!f.test(a[i])) {
			for (int j = a[i]; j <= m; j++) {
				if (f.test(j - a[i])) {
					f.set(j);
				}
			}
			ans++;
		}
	}
	printf("%d\n", ans);
}

int main() {
	freopen("money.in", "r", stdin);
	freopen("money.out", "w", stdout);
	scanf("%d", &T);
	while (T--) {
		solve();
	}
	return 0;
}

Problem C

　　考虑二分答案。考虑在每个子树内决策，每个子树内最多有一条未完成的路径对父节点有贡献。

　　首先需要最大化数量，不难证明这样不会更劣。

　　首先已经满足条件的可以直接算入答案，没有满足条件考虑两两配对。这个从大的开始考虑，每次和最小的能够匹配的配对。

　　考虑如何在数量最大的情况下，最大化对父节点的贡献。考虑最大没有匹配的路径，考虑用它替换掉某组匹配中的较大值。

　　时间复杂度 $O(n\log V\log n)$。

Code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <vector>
using namespace std;
typedef bool boolean;

template <typename T>
void pfill(T* pst, const T* ped, T val) {
	for ( ; pst != ped; *(pst++) = val);
}

typedef class Edge {
	public:
		int ed, nx, w;

		Edge(int ed = 0, int nx = 0, int w = 0):ed(ed), nx(nx), w(w) {	}
}Edge;

typedef class MapManager {
	public:
		int ce;
		int* h;
		Edge* es;

		MapManager() : ce(-1), h(NULL), es(NULL) {	}
		MapManager(int n, int m) : ce(-1) {
			h = new int[(n + 1)];
			es = new Edge[(m + 1)];
			pfill(h, h + n + 1, -1);
		}	

		void addEdge(int u, int v, int w) {
			es[++ce] = Edge(v, h[u], w);
			h[u] = ce;
		}

		Edge& operator [] (int p) {
			return es[p];
		}
}MapManager;

template <typename T>
class Pool {
	public:
		int sz;
		T *p;
		T *tp;

		Pool(int sz) : sz(sz) {
			p = new T[sz + 1];
			tp = p;
		}

		void reset() {
			tp = p;
		}

		T* alloc(int len) {
			T* rt = tp;
			tp += len;
//			cerr << tp - p << '\n';
			return rt;
		}
};

typedef pair<int, int> pii;

const int N = 5e4 + 3;

int n, m;
int deg[N];
MapManager g;
Pool<int> pl1(N << 2);
Pool<pii> pl2(N << 2);
Pool<boolean> pl3(N << 2);

inline void init() {
	scanf("%d%d", &n, &m);
	g = MapManager(n, n << 1);
	pfill(deg + 1, deg + n + 1, 0);
	for (int i = 1, u, v, w; i < n; i++) {
		scanf("%d%d%d", &u, &v, &w);
		g.addEdge(u, v, w);
		g.addEdge(v, u, w);
		deg[u]++, deg[v]++;
	}
}

//int cnt;
pii dfs(int p, int fa, int mid) {
	int* a = pl1.alloc(deg[p] + 1);
	pii* m = pl2.alloc(deg[p] + 1);
	boolean* vis = pl3.alloc(deg[p] + 1);
//	cerr << ++cnt << '\n';

	int rt = 0, tp = 0;
	for (int i = g.h[p], e; ~i; i = g[i].nx) {
		 if ((e = g[i].ed) == fa)
			 continue;
		 pii x = dfs(e, p, mid);
		 rt += x.first, a[++tp] = (x.second + g[i].w);
	}

	sort(a + 1, a + tp + 1);
	while (tp && a[tp] >= mid)
		tp--, rt++;

	if (!tp)
		return pii(rt, 0);

	for (int i = 0; i <= tp; i++)
		vis[i] = false;

	int l = 1, r = tp, _tp = 0;
	while (l < r) {
		while (l < r && a[l] + a[r] < mid)
			l++;
		if (l < r) {
			m[++_tp] = pii(a[l], a[r]);
			vis[l] = vis[r] = true;
			l++, r--, rt++;
		}
	}

	while (r && vis[r])
		r--;

	if (!r)
		return pii(rt, 0);

	int b = a[r];
	for (int i = _tp; i; i--)
		if (m[i].first + b >= mid)
			return pii(rt, m[i].second);
	return pii(rt, b);
}

boolean check(int mid) {
//	cnt = 0;
	pl1.reset();
	pl2.reset();
	pl3.reset();
	return dfs(1, 0, mid).first >= m;
}

inline void solve() {
	int l = 1, r = 5e8, mid;
	while (l <= r) {
		mid = (l + r) >> 1;
		if (check(mid))
			l = mid + 1;
		else
			r = mid - 1;
	}
	printf("%d\n", l - 1);
}

int main() {
	freopen("track.in", "r", stdin);
	freopen("track.out", "w", stdout);
	init();
	solve();
	return 0;
}

Day 2

Problem A

　　暴力枚举断掉环上的哪一条边。

Code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <vector>
#include <stack>
using namespace std;
typedef bool boolean;

const int N = 5005;

int n, m;
int tp;
int ans[N];
int cmp[N];
vector<int> g[N];

inline void init() {
	scanf("%d%d", &n, &m);
	for (int i = 1, u, v; i <= m; i++) {
		scanf("%d%d", &u, &v);
		g[u].push_back(v);
		g[v].push_back(u);
	}
}

namespace tree {

void dfs(int p, int fa) {
	ans[++tp] = p;
	for (int i = 0, e; i < (signed) g[p].size(); i++)
		if ((e = g[p][i]) ^ fa)
			dfs(e, p);
}

inline void solve() {
	tp = 0;
	for (int i = 1; i <= n; i++)
		sort(g[i].begin(), g[i].end());
	dfs(1, 0);
	for (int i = 1; i <= n; i++)
		printf("%d%c", ans[i], (i == n) ? ('\n') : (' '));
}

}

namespace circle {

stack<int> s;
boolean vis[N];
vector<int> cir;

boolean dfs1(int p, int fa) {
	if (vis[p]) {
		int cur;
		do {
			cur = s.top();
			s.pop();
			cir.push_back(cur);
		} while (cur != p);
		return true;
	}
	s.push(p), vis[p] = true;
	for (int i = 0, e; i < (signed) g[p].size(); i++)
		if (((e = g[p][i]) ^ fa) && dfs1(e, p))
			return true;
	s.pop();
	return false;
}

void dfs(int p, int fa, int banu, int banv) {
	cmp[++tp] = p;
//	cerr << p << " " << tp << '\n';
	boolean sgn1 = (p == banu || p == banv);
	for (int i = 0, e; i < (signed) g[p].size(); i++) {
		e = g[p][i];
		if ((e ^ fa) && !(sgn1 && (e == banu || e == banv)))
			dfs(e, p, banu, banv);
	}
}

boolean check_update() {
	for (int i = 1; i <= n; i++)
		if (ans[i] ^ cmp[i])
			return cmp[i] < ans[i];
	return false;
}

inline void solve() {
	for (int i = 1; i <= n; i++)
		sort(g[i].begin(), g[i].end());
	dfs1(1, 0);
	signed int s = (signed) cir.size();
	tp = 0;
	dfs(1, 0, cir[0], cir[1]);
	for (int j = 1; j <= n; j++)
		ans[j] = cmp[j];
	for (int i = 1; i < s; i++) {
//		cerr << cir[i] << '\n';
		tp = 0;
		dfs(1, 0, cir[i], cir[(i + 1) % s]);
		if (check_update())
			for (int j = 1; j <= n; j++)
				ans[j] = cmp[j];
	}
	for (int i = 1; i <= n; i++)
		printf("%d%c", ans[i], (i == n) ? ('\n') : (' '));
}

}

int main() {
	freopen("travel.in", "r", stdin);
	freopen("travel.out", "w", stdout);
	init();
	if (n == m)
		circle :: solve();
	else
		tree :: solve();
	return 0;
}

　　好像校内 oj 上测，最慢一个点 978ms，Emm......

　　其实考虑在环上每一个位置往回走的下一个标号是确定的。然后就能 $O(n\log n)$ 了。

　　最近手残得比较厉害，sad.....

Code

#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;

const int N = 5e3 + 5;

int n, m;
vector<int> ans;
vector<int> G[N];

void dfs(int p, int fa, vector<int> &ans = ::ans) {
	ans.push_back(p);
	for (int _ = 0, e; _ < (signed) G[p].size(); _++) {
		if ((e = G[p][_]) ^ fa) {
			dfs(e, p);
		}
	}
} 

boolean vis[N];
vector<int> cir;
boolean findcir(int p, int fa) {
	if (vis[p]) {
		vector<int>::iterator it = --cir.end();
		while (*it ^ p)
			it--;
		cir.erase(cir.begin(), it);
		return true;
	}
	vis[p] = true;
	cir.push_back(p);
	for (int _ = 0, e; _ < (signed) G[p].size(); _++) {
		if (((e = G[p][_]) ^ fa) && findcir(e, p)) {
			return true;
		}
	}
	cir.pop_back();
	return false;
}

void finderase(vector<int>& a, int x) {
	vector<int>::iterator it = a.begin();
	while (*it ^ x)
		it++;
	a.erase(it);
}

int main() {
	freopen("travel.in", "r", stdin);
	freopen("travel.out", "w", stdout);
	scanf("%d%d", &n, &m);
	for (int i = 1, u, v; i <= m; i++) {
		scanf("%d%d", &u, &v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	for (int i = 1; i <= n; i++)
		sort(G[i].begin(), G[i].end());
	if (n == m) {
		findcir(1, 0);
		int nxt = *upper_bound(G[cir[0]].begin(), G[cir[0]].end(), cir[1]);
		for (int i = 1, x, y; ; i++) {
			x = cir[i];
			if (x >= nxt) {
				y = cir[i - 1];
				finderase(G[x], y);
				finderase(G[y], x);
//				cerr << x << " " << y << " " << nxt << '\n';
				break;
			}
			vector<int>::iterator it = upper_bound(G[x].begin(), G[x].end(), cir[i + 1]);
			if (it != G[x].end() && *it == cir[i - 1])
				it++;
			if (it != G[x].end())
				nxt = *it;
		}
	}
	dfs(1, 0, ans);
	for (int i = 0; i < n; i++)
		printf("%d ", ans[i]);
	return 0;
}

Problem B

　　请欣赏神仙行为：

• 早上教练发题，神仙 jerome_wei 说难道这题能做，下午发成绩，rk 1 cdqz-wyp 100 100 100 300
• 早上教练发题，神仙 jerome_wei 说咕了咕了，下午发成绩，rk 1 cdqz-wyp 100 100 100 300
• 一天，神仙  jerome_wei 看到了这道题，说这什么鬼题，跑了跑了，不久之后博客上出现了详细题解和证明

---

　　不难发现 $a_{x, y} \geqslant a_{x - 1, y + 1}$。

　　考虑一处不合法的路径，如果存在一定是字典序相邻的一对，这样话就是考虑把最后一个不在最后一行的 R 替换成 D，大概是这样的：

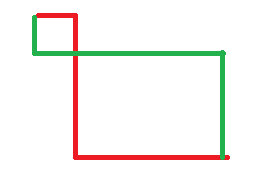
　　你发现如果第二个位置相等，由于在另一条路径下方的权值一定是小于等于它的，由此可以推出它们字典序相等。那么右下角的大矩形内每一对 $x + y$ 相等的 $a_{x, y}$ 都是相同的。

　　随便 dp 一下应该能拿到 65 分的好成绩。（枚举 $x + y$ 的值，状压一下当前的满足 $a_{x, y} = a_{x - 1, y + 1}$ 以及横纵坐标和等于 $x + y + 1$ 的状态）

　　不难注意到，当 $m$ 比较大的时候，中间的有效状态只有常数个，考虑 $x = 0, 1$ 总是可行的，当 $x \geqslant 3, y \geqslant 2$ 的时候，这些格子必须满足 $a_{x, y} = a_{x - 1, y + 1}$。因为：

　　因为红格子和蓝格子以及蓝格子和黄格子不可能同时都不同。

　　理论上中间暴力 dp 能过，不过写个矩乘快速幂怎么都能过，我好像有地方写菜了，然后好像就过不了？因为我非常地懒，众所周知，打表可得当 $m \geqslant n + 1$ 的时候当 $m$ 每增加 1，答案乘上 3。

　　如果我 csp 后没退役再来填这个规律的坑好了。

Code

#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;

#define ll long long

void exgcd(int a, int b, int& x, int& y) {
	if (!b) {
		x = 1, y = 0;
	} else {
		exgcd(b, a % b, y, x);
		y -= (a / b) * x;
	}
}

int inv(int a, int n) {
	int x, y;
	exgcd(a, n, x, y);
	return (x < 0) ? (x + n) : (x);
}

const int Mod = 1e9 + 7;

template <const int Mod = :: Mod>
class Z {
	public:
		int v;

		Z() : v(0) {	}
		Z(int x) : v(x){	}
		Z(ll x) : v(x % Mod) {	}

		friend Z operator + (const Z& a, const Z& b) {
			int x;
			return Z(((x = a.v + b.v) >= Mod) ? (x - Mod) : (x));
		}
		friend Z operator - (const Z& a, const Z& b) {
			int x;
			return Z(((x = a.v - b.v) < 0) ? (x + Mod) : (x));
		}
		friend Z operator * (const Z& a, const Z& b) {
			return Z(a.v * 1ll * b.v);
		}
		friend Z operator ~(const Z& a) {
			return inv(a.v, Mod);
		}
		friend Z operator - (const Z& a) {
			return Z(0) - a;
		}
		Z& operator += (Z b) {
			return *this = *this + b;
		}
		Z& operator -= (Z b) {
			return *this = *this - b;
		}
		Z& operator *= (Z b) {
			return *this = *this * b;
		}
		friend boolean operator == (const Z& a, const Z& b) {
			return a.v == b.v;
		}
};

Z<> qpow(Z<> a, int p) {
	Z<> rt = Z<>(1), pa = a;
	for ( ; p; p >>= 1, pa = pa * pa) {
		if (p & 1) {
			rt = rt * pa;
		}
	}
	return rt;
}

typedef Z<> Zi;

#define pii pair<int, int>

const int N = 1e6 + 10;

int n, m;
int Lx[N], Rx[N];
map<pii, Zi> G[N];

int opt(int sum, int s, int x) {
	if (x <= Lx[sum] || x > Rx[sum])
		return s;
	return s | (1 << x);
}

Zi dp(int sum, int s0, int s1) {
	if (sum == n + m - 2)
		return 2;
	if (G[sum].count(pii(s0, s1))) {
		return G[sum][pii(s0, s1)];
	}
	Zi rt = 0;
	int ns0 = s1;
	for (int i = Lx[sum]; i <= Rx[sum]; i++) {
		if ((s0 >> i) & 1) {
			ns0 = opt(sum + 1, ns0, i);
			ns0 = opt(sum + 1, ns0, i + 1);
		}
	}
	for (int i = Lx[sum]; i <= Rx[sum] + 1; i++) {
		if ((s0 >> i) & 1)
			continue;
		int ns1 = 0;
		for (int j = Lx[sum] + 1; j <= i && j <= Rx[sum]; j++)
			ns1 = opt(sum + 2, ns1, j + 1);
		for (int j = i + 2; j <= Rx[sum]; j++)
			ns1 = opt(sum + 2, ns1, j + 1);
		rt += dp(sum + 1, ns0, ns1);
	}
//	cerr << sum << " " << s0 << " " << s1 << " " << rt.v << '\n';
	return G[sum][pii(s0, s1)] = rt;
}

Zi solve(int n, int m) {
	if (n > m)
		swap(n, m);
	if (n == m || m == n + 1) {
		::n = n, ::m = m;
		for (int i = 0; i < m + 10; i++) {
			Lx[i] = 20, Rx[i] = 0;
		}
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				Lx[i + j] = min(Lx[i + j], i);
				Rx[i + j] = max(Rx[i + j], i);
			}
		}
		return dp(0, 0, 0);
	}
	if (n == 1)
		return qpow(2, m);
	return solve(n, n + 1) * qpow(3, m - n - 1);
}

int main() {
	freopen("game.in", "r", stdin);
	freopen("game.out", "w", stdout);
	scanf("%d%d", &n, &m);
	printf("%d\n", solve(n, m).v);
	return 0;
}

Problem C

　　ddp 板题。

　　考察选手能否熟练地敲打 ddp 板子。

Code

#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;

const int N = 1e5 + 5;

#define ll long long

template <typename T>
T smin(T a, T b) {
	return min(a, b);
}
template <typename T, typename ...Q>
T smin(T a, const Q &...args) {
	return min(a, smin(args...));
}

const ll llf = 1e12;

typedef class Data {
	public:
		ll a[2][2];

		Data() {	}
		Data(ll x) {
			a[0][0] = llf, a[0][1] = 0;
			a[1][0] = x, a[1][1] = x;
		}
		Data(ll x, ll y, ll z, ll w) {
			a[0][0] = x, a[0][1] = y;
			a[1][0] = z, a[1][1] = w;
		}

		Data get() {
			ll g = min(a[0][0], a[0][1]);
			ll f = min(a[1][0], a[1][1]);
			g = min(g, f);
			return Data(f, f, g, g);
		}
		ll* operator [] (int p) {
			return a[p];
		}
		friend Data operator * (Data a, Data b) {
			Data rt;
			rt[0][0] = min(a[0][0] + b[0][0], a[0][1] + b[1][0]);
			rt[0][1] = min(a[0][0] + b[0][1], a[0][1] + b[1][1]);
			rt[1][0] = min(a[1][0] + b[0][0], a[1][1] + b[1][0]);
			rt[1][1] = min(a[1][0] + b[0][1], a[1][1] + b[1][1]);
			return rt;
		}
		friend Data operator + (Data a, Data b) {
			Data rt;
			rt[0][0] = a[0][0] + b[0][0];
			rt[0][1] = a[0][1] + b[0][1];
			rt[1][0] = a[1][0] + b[1][0];
			rt[1][1] = a[1][1] + b[1][1];
			return rt;
		}
		friend Data operator - (Data a, Data b) {
			Data rt;
			rt[0][0] = a[0][0] - b[0][0];
			rt[0][1] = a[0][1] - b[0][1];
			rt[1][0] = a[1][0] - b[1][0];
			rt[1][1] = a[1][1] - b[1][1];
			return rt;
		}
		ll get_ans() {
			ll rt = smin(a[0][0], a[0][1], a[1][0], a[1][1]);
			return (rt >= llf) ? (-1) : (rt);
		}
} Data;

typedef class SegTreeNode {
	public:
		Data d;
		SegTreeNode *fa;
		SegTreeNode *l, *r;

		void push_up() {
			d = l->d * r->d;
		}
} SegTreeNode;

typedef class Chain {
	public:
		SegTreeNode *st;
		int len, top;

		Chain() {	}
		Chain(int top);

		void update(int, Data, Data);
} Chain;

SegTreeNode pool[N << 1];
SegTreeNode *_top = pool;

int S[N];
Data dat[N];

int tp;
Chain *ch[N];
SegTreeNode *tr[N];

void build(SegTreeNode*& p, int l, int r) {
	p = _top++;
	if (l == r) {
		p->d = dat[S[l]];
		tr[S[l]] = p;
		return;
	}
	int mid = (l + r) >> 1;
	build(p->l, l, mid);
	build(p->r, mid + 1, r);
	p->push_up();
	p->l->fa = p;
	p->r->fa = p;
}

Chain::Chain(int top) : st(_top), len(tp), top(top) {
	reverse(S + 1, S + tp + 1);
	build(st, 1, len);
	for (int i = 1; i <= len; i++) {
		ch[S[i]] = this;
	}
	if (top) {
		dat[top] = dat[top] + st->d.get();
	}
}

void Chain::update(int x, Data old_d, Data new_d) {
	Data nold_d = st->d.get();
	tr[x]->d = tr[x]->d - old_d + new_d;
	for (SegTreeNode *p = tr[x]->fa; p; p = p->fa)
		p->push_up();
	if (top) {
		ch[top]->update(top, nold_d, st->d.get());
	}
}

int n, m;
int p[N];
int sz[N], zson[N];
vector<int> G[N];

void dfs1(int p, int fa) {
	int mx = 0, &id = zson[p];
	sz[p] = 1;
	for (auto e : G[p]) {
		if (e ^ fa) {
			dfs1(e, p);
			sz[p] += sz[e];
			if (mx < sz[e]) {
				mx = sz[e];
				id = e;
			}
		}
	}
}

void dfs2(int p, int fa) {
	if (zson[p]) {
		for (auto e : G[p]) {
			if ((e ^ fa) && (e ^ zson[p])) {
				dfs2(e, p);
				new Chain(p);
			}
		}
		dfs2(zson[p], p);
	} else {
		tp = 0;
	}
	S[++tp] = p;
}

int main() {
	freopen("defense.in", "r", stdin);
	freopen("defense.out", "w", stdout);
	scanf("%d%d%*s", &n, &m);
	for (int i = 1, x; i <= n; i++) {
		scanf("%d", &x);
		dat[i] = x;
		p[i] = x;
	}
	for (int i = 1, u, v; i < n; i++) {
		scanf("%d%d", &u, &v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	dfs1(1, 0);
	dfs2(1, 0);
	new Chain(0);
	int a, x, b, y;
	while (m--) {
		scanf("%d%d%d%d", &a, &x, &b, &y);
		Data olda = p[a], oldb = p[b];
		Data na = Data(llf * (1 - x)), nb = Data(llf * (1 - y));
		ch[a]->update(a, olda, na);
		ch[b]->update(b, oldb, nb);
		ll ans = ch[1]->st->d.get_ans() + olda[1][0] * x + oldb[1][0] * y;
		ch[a]->update(a, na, olda);
		ch[b]->update(b, nb, oldb);
		printf("%lld\n", ans);
	}
	return 0;
}