SP375 QTREE - Query on a tree (树剖)

题目

SP375 QTREE - Query on a tree

解析

也就是个蓝题，因为比较长

树剖裸题（基本上），单点修改，链上查询。

顺便来说一下链上操作时如何将边上的操作转化为点上的操作：

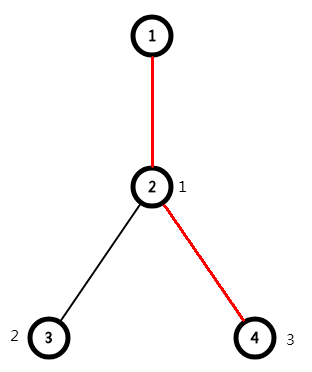
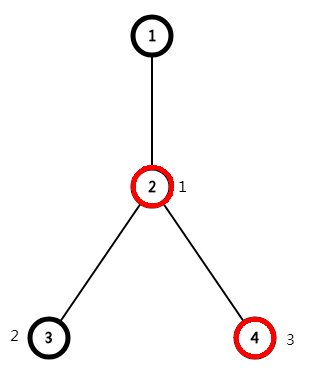
可以看到这个题然我们对边进行操作，我们的树剖是对节点进行操作的，所以我们考虑把边权变为点权。



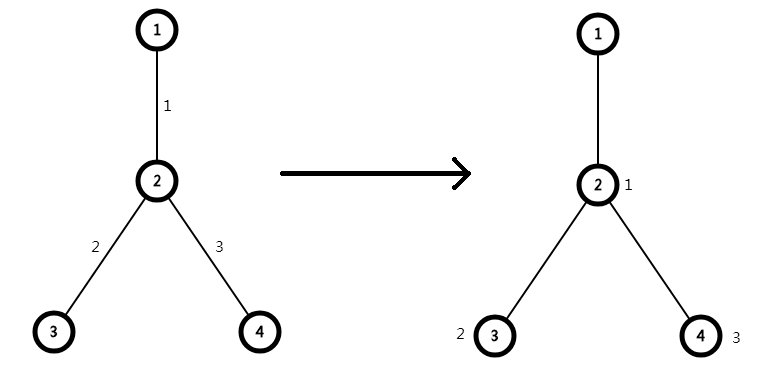
发现我们节点的点权是连向它的边的边权，所以我们要操作边权的话，我们操作的实际上是其连向点的点权，

假设我们要修改1-4之间的这两条边



我们修改的实际上就是这2,4两个点



我们节点的点权为其父节点连向它的边的边权，所以我们链上修操作的时候，不要操作深度较低的节点，因为它代表的边是它的父节点连向它的那一条，不是要操作的两点之间的边，就像上图我们不操作1号节点一样。

不用特意判断；两个位置的深浅，树剖中会判断，详见这里

再说一下这个题的修改，因为我们是要修改边权，我们的边权给了点，所以我们找一下这条边连的两个点，判断两个点的深度，较深的那个是我们要修改的点。

然后这是SPOJ上的题，我不知道为啥我写c++会挂，经king丨帝御威大佬的指点才用c过的,%%%

代码

#include <ctype.h>
#include <stdio.h>
#include <limits.h>
#include <stdlib.h>
#include <string.h>
#define lson rt << 1
#define rson rt << 1 | 1
#define N 10007
int t, n, m, num, cnt;
int head[N], a[N], w[N], son[N], size[N], f[N], top[N], dep[N], id[N], mx[N << 2];
class node {
	public :
		int nx, v, w;
} e[N << 2];
void add(int u, int v, int w) {
	e[++num].nx = head[u], e[num].v = v, e[num].w = w, head[u] = num;
}
int max(int a, int b) { return a > b ? a : b; }
#define swap(A, B)   \
    {                \
        int __T = A; \
        A = B;       \
        B = __T;     \
    }
void dfs1(int u, int fa) {
	size[u] = 1;
	for (int i = head[u]; ~i; i = e[i].nx) {
		int v = e[i].v;
		if (v != fa) {
			dep[v] = dep[u] + 1;
			f[v] = u;
			w[v] = e[i].w;	//边权赋给点
			dfs1(v, u);
			size[u] += size[v];
			if (size[v] > size[son[u]]) son[u] = v;
		}
	}
}
void dfs2(int u, int t) {
	id[u] = ++cnt;
	a[cnt] = w[u];
	top[u] = t;
	if (son[u]) dfs2(son[u], t);
	for (int i = head[u]; ~i; i = e[i].nx) {
		int v = e[i].v;
		if (v != f[u] && v != son[u]) dfs2(v, v);
	}
}
void pushup(int rt) {
	mx[rt] = max(mx[lson], mx[rson]);
}
void build(int l, int r, int rt) {
	if (l == r) {
		mx[rt] = a[l];
		return ;
	}
	int m = (l + r) >> 1;
	build(l, m, lson);
	build(m + 1, r, rson);
	pushup(rt);
}
void update(int L, int c, int l, int r, int rt) {
	if (l == r) {
		mx[rt] = c;
		return ;
	}
	int m = (l + r) >> 1;
	if (L <= m) update(L, c, l, m, lson);
	else update(L, c, m + 1, r, rson);
	pushup(rt);
}
int query(int L, int R, int l, int r, int rt) {
	if (L <= l && r <= R) return mx[rt];
	int m = (l + r) >> 1, ans = -0x3f3f3f3f;
	if (L <= m) ans = max(ans, query(L, R, l, m, lson));
	if (R > m) ans = max(ans, query(L, R, m + 1, r, rson));
	return ans;
}
int query_chain(int x, int y) {
	int fx = top[x], fy = top[y], ans = -0x3f3f3f3f;
	while (fx != fy) {
		if (dep[fx] < dep[fy]) {
			swap(x, y);
			swap(fx, fy);
		}
		ans = max(ans, query(id[fx], id[x], 1, cnt, 1));
		x = f[fx], fx = top[x];
	}
	if (id[x] > id[y]) swap(x, y);
	ans = max(ans, query(id[x] + 1, id[y], 1, cnt, 1));
	/*在这里注意是id[x]+1->id[y]，不要算上深度较浅的点*/
	return ans;
}
int main() {
	scanf("%d", &t);
	while (t -- ) {
		num = cnt = 0;
		memset(head, -1, sizeof(head));
		memset(dep, 0, sizeof(dep));
		memset(id, 0, sizeof(id));
		memset(a, 0, sizeof(a));
		memset(w, 0, sizeof(w));
		memset(top, 0, sizeof(top));
		memset(size, 0, sizeof(size));
		memset(e, 0, sizeof(e));
		memset(mx, 0, sizeof(mx));
		memset(son, 0, sizeof(son));
		memset(f, 0, sizeof(f));
		scanf("%d", &n);
		for (int i = 1, x, y, z; i < n; ++i) {
			scanf("%d%d%d", &x, &y, &z);
			add(x, y, z), add(y, x, z);
		}
		dfs1(1, 0), dfs2(1, 1);
		build(1, n, 1);
		char s[20];
		int x, y;
		while (1) {
			scanf("%s", s);
			if (s[0] == 'D') break;
			else if (s[0] == 'C') {
				scanf("%d%d", &x, &y);
				x = dep[e[x << 1].v] > dep[e[(x << 1) - 1].v] ? e[x << 1].v : e[(x << 1) - 1].v;
				/*因为是无向边，加了两次，两次的v都不是一个点*/
				update(id[x], y, 1, n, 1);
			} else {
				scanf("%d%d", &x, &y);
				printf("%d\n", query_chain(x, y));
			}
		}
	}
	return 0;
}