【Luogu】P3380树套树模板（线段树套Splay）

　　题目链接

　　幸甚至哉，歌以咏志。

　　拿下了曾经是那么遥不可及的线段树，学会了曾经高不可攀的平衡树，弄懂了装B的时候才挂在嘴边的树套树。

　　每道模板都是链上的一颗珠子。把它们挨个串起来，就成为我成长的历程。

　　抒情结束开始讲题

　　这道题我们用线段树存平衡树的根节点。比如我们有一棵线段树

　　

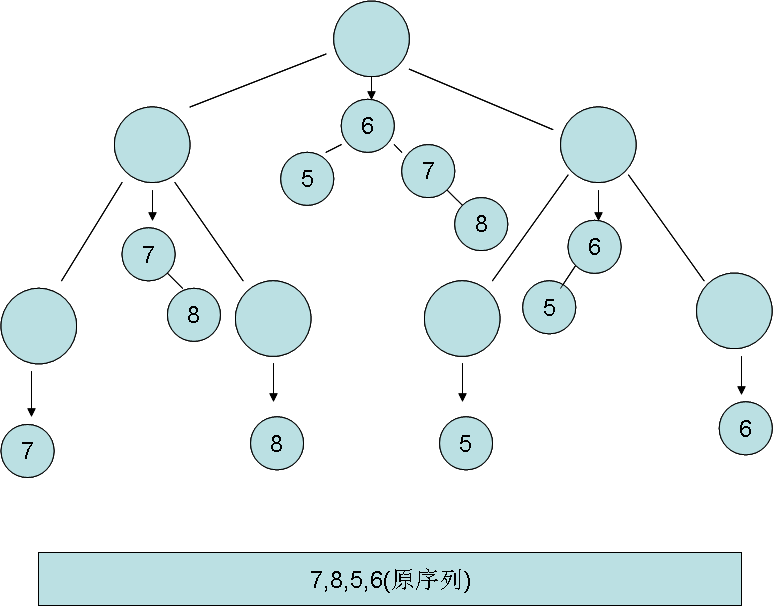
　　这样子。线段树的一个节点   存   它表示的那个区间   所对应的  平衡树   的根节点编号。这样每个节点都拥有一棵平衡树。是不是很炫呢？

　　对于操作1我们就可以把所有零散的区间里比它小的数的个数都找出来，+1就是答案啦。

　　对于操作2我们可以二分数，然后不断地进行操作1.

　　对于操作3我们用logn的时间把所有包含这个点的区间都修改一遍。

　　对于操作4和操作5，不多讲了。

　　很炫吧

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cctype>
#define mid ((l+r)>>1)
#define left (rt<<1)
#define right (rt<<1|1)
#define lson l,mid,left
#define rson mid+1,r,right

using std::max;
using std::min;

inline int read(){
    int num=,f=;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')    f=-;
        ch=getchar();
    }
    while(isdigit(ch)){
        num=num*+ch-'';
        ch=getchar();
    }
    return num*f;
}

int s[];
int q[];

struct Node{
    int e[],fa,val,size,sum;
}tree[];
int tot,point;
inline void update(int x){
    tree[x].size=tree[x].sum;
    if(tree[x].e[])    tree[x].size+=tree[tree[x].e[]].size;
    if(tree[x].e[])    tree[x].size+=tree[tree[x].e[]].size;
}
inline void connect(int x,int fa,int how){    tree[x].fa=fa;    tree[fa].e[how]=x;    }
inline int iden(int x){    return x==tree[tree[x].fa].e[];    }
void rotate(int x,int rt){
    int y=tree[x].fa;    int r=tree[y].fa;
    if(y==s[rt])    s[rt]=x;
    int sony=iden(x);    int sonr=iden(y);
    int b=tree[x].e[sony^];
    connect(b,y,sony);
    connect(y,x,sony^);
    connect(x,r,sonr);
    update(y);    update(x);
}

void splay(int pos,int to,int rt){
    to=tree[to].fa;
    while(tree[pos].fa!=to){
        if(tree[tree[pos].fa].fa==to)    rotate(pos,rt);
        else
            if(iden(pos)==iden(tree[pos].fa)){    rotate(tree[pos].fa,rt);    rotate(pos,rt);    }
            else    {    rotate(pos,rt);    rotate(pos,rt);    }
    }
}

inline int create(int val,int fa){
    tree[++tot].val=val;
    tree[tot].fa=fa;
    tree[tot].sum=tree[tot].size=;
    return tot;
}

inline void Delete(int x){
    tree[x].e[]=tree[x].e[]=;
    if(x==tot)    tot--;
}

int build(int val,int rt){
    point++;
    if(!s[rt]){    s[rt]=create(val,);    return s[rt];}
    else{
        int now=s[rt];
        while(){
            tree[now].size++;
            if(val==tree[now].val){    tree[now].sum++;    return now;    }
            int nxt=val<tree[now].val?:;
            if(!tree[now].e[nxt]){
                create(val,now);
                tree[now].e[nxt]=tot;
                return tot;
            }
            now=tree[now].e[nxt];
        }
    }
    return ;
}

inline void insert(int val,int rt){
    int p=build(val,rt);
    splay(p,s[rt],rt);
}

int find(int val,int rt){
    int now=s[rt];
    while(now){
        if(tree[now].val==val){    splay(now,s[rt],rt);    return now;    }
        int nxt=val>tree[now].val;
        if(!tree[now].e[nxt])    return ;
        now=tree[now].e[nxt];
    }
}

void pop(int val,int rt){
        int deal=find(val,rt);
        if(!deal)    return;
        point--;
        if(tree[deal].sum>){    tree[deal].sum--;    tree[deal].size--;    return;    }
        if(!tree[deal].e[]){    s[rt]=tree[deal].e[];    tree[s[rt]].fa=;    }
        else{
            int le=tree[deal].e[];
            while(tree[le].e[])    le=tree[le].e[];
            splay(le,tree[deal].e[],rt);
            int ri=tree[deal].e[];
            connect(ri,le,);    s[rt]=le;
            update(le);
        }
        Delete(deal);
}

int rank(int val,int rt){
    int ans=,now=s[rt];
    while(){
        //printf("%d %d\n",now,tree[now].sum);
        if(val<tree[now].val){
            now=tree[now].e[];
            if(!now)    return ans;
        }
        else{
            if(tree[now].e[])    ans+=tree[tree[now].e[]].size;
            if(val==tree[now].val||!tree[now].e[]){
                if(val>tree[now].val)    ans+=tree[now].sum;
                splay(now,s[rt],rt);
                return ans;
            }
            ans+=tree[now].sum;    now=tree[now].e[];
        }
    }
}

inline int lower(int val,int rt){
    int ans=-,now=s[rt];
    while(){
        if(!now)    return ans;
        if(tree[now].val<val&&tree[now].val>ans)    ans=tree[now].val;
        int nxt=val>tree[now].val?:;
        now=tree[now].e[nxt];
    }
}

inline int upper(int val,int rt){
    int ans=,now=s[rt];
    while(){
        if(!now)    return ans;
        if(tree[now].val>val&&tree[now].val<ans)    ans=tree[now].val;
        int nxt=val>tree[now].val?:;
        now=tree[now].e[nxt];
    }
}

int lows(int val,int rt){
    int ans=-,now=s[rt];
    while(){
        if(!now)    return ans;
        if(tree[now].val<=val&&tree[now].val>ans)    ans=tree[now].val;
        if(tree[now].val==val)    return ans;
        int nxt=val>tree[now].val?:;
        now=tree[now].e[nxt];
    }
}

void Build(int l,int r,int rt){
    if(l>r)    return;
    if(l==r){
        insert(q[l],rt);
        return;
    }
    Build(lson);
    Build(rson);
    for(int i=l;i<=r;++i)    insert(q[i],rt);
    return;
}

int findrank(int from,int to,int num,int l,int r,int rt){
    if(from<=l&&to>=r)    return rank(num,rt);
    int ans=;
    if(from<=mid)    ans+=findrank(from,to,num,lson);
    if(to>mid)        ans+=findrank(from,to,num,rson);
    return ans;
}

void Update(int o,int num,int l,int r,int rt){
    pop(q[o],rt);
    insert(num,rt);
    if(l==r)    return;
    if(o<=mid)    Update(o,num,lson);
    else        Update(o,num,rson);
}

int findlower(int from,int to,int num,int l,int r,int rt){
    if(from<=l&&to>=r)    return lower(num,rt);
    int ans=-;
    if(from<=mid)    ans=max(ans,findlower(from,to,num,lson));
    if(to>mid)        ans=max(ans,findlower(from,to,num,rson));
    return ans;
}

int findupper(int from,int to,int num,int l,int r,int rt){
    if(from<=l&&to>=r)    return upper(num,rt);
    int ans=;
    if(from<=mid)    ans=min(ans,findupper(from,to,num,lson));
    if(to>mid)        ans=min(ans,findupper(from,to,num,rson));
    return ans;
}

int main(){
    int n=read(),m=read();
    for(int i=;i<=n;++i)    q[i]=read();
    Build(,n,);
    for(register int i=;i<=m;++i){
        int opt=read();
        if(opt==){
            int l=read(),r=read(),q=read();
            printf("%d\n",findrank(l,r,q,,n,)+);
        }
        else if(opt==){
            int l=read(),r=read(),q=read();
            int a=,b=1e8,Ans=;
            while(a<=b){
                int m=(a+b)>>;
                int x=lows(m,);
                if(findrank(l,r,x,,n,)+>q)    b=m-;
                else{
                    a=m+;
                    Ans=x;
                }
            }
            printf("%d\n",Ans);
        }
        else if(opt==){
            int l=read(),r=read();
            Update(l,r,,n,);
            q[l]=r;
        }
        else if(opt==){
            int l=read(),r=read(),q=read();
            printf("%d\n",findlower(l,r,q,,n,));
        }
        else if(opt==){
            int l=read(),r=read(),q=read();
            printf("%d\n",findupper(l,r,q,,n,));
        }
    }
    return ;
}