HNOI2008 明明的烦恼 （purfer序列 + 组合数学）

传送门

这道题题意描述很清楚，不过我自己做的时候确实是一头雾水……又看了题解，发现要用到一个新知识，叫purfer序列。

我们来简单说一下什么是purfer序列。它可以被看作一种树的表现形式。一棵含有n个节点的树可以用一个长度为n-2的purfer序列表示，而其中每一个树都是1～n之间的一个数。

每一棵树，它都有自己唯一的purfer序列，反过来，对于每一个purfer序列，都能获得唯一的一棵树。也就是说，树与其purfer序列一一对应。

先说一下怎么求purfer序列。首先找出这棵树中，节点编号数最小的一个叶子结点（度数为1，只有连向其父亲的一条边），把与它相连的那个节点加入到purfer序列中，并且将这个节点和与之相连的边从这棵树中删除。重复上述过程n-2步，得到一个长度为n-2的purfer序列和一个只有两个节点的树。

（还是偷一下大神的图来描述这件事）

看看下面的例子：

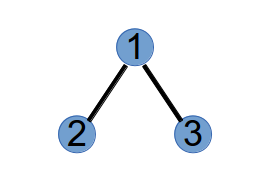
假设有一颗树有 5 个节点，四条边依次为：(1, 2), (1, 3), (2, 4), (2, 5)，如下图所示：

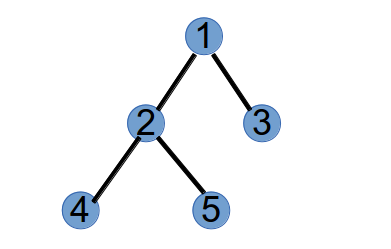
第 1 步，选取具有最小标号的叶子节点 3，将与它相连的点 1 作为第 1 个 Purfer Number，并从树中删掉节点 3：

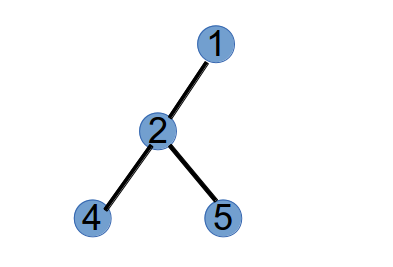
第 2 步，选取最小标号的叶子节点 1，将与其相连的点 2 作为第 2 个 Purfer Number，并从树中删掉点 1：

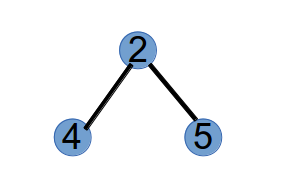
第 3 步，选取最小标号的叶子节点 4，将与其相连的点 2 作为第 3 个 Purfer Number，并从树中删掉点 4：

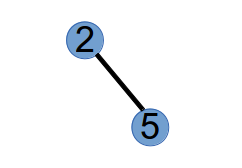
最后，我们得到的 Purfer Sequence 为：1 2 2

既然如此，purfer序列就求好了，那我们再说一下怎么通过purfer序列求它相对应的树。

先把所有节点的度数赋为1，再加上其在Purfer序列中出现过的次数，得到每一个节点的度。每次选取编号最小的度数为1的节点（比如当前枚举到第i个点），将这个节点和Purfer序列中第i个数所对应的点连一条边，并且把这两个点的度数-1。最后得到两个度数为1的点，我们再把他们连边，加入到树中。这样就成功的通过purfer序列求出一棵树了。

（我们再偷一次大神的图并且以上面的例子为例描述一下这个过程）（感谢大神orz）

顶点	1	2	3	4	5
度	2	3	1	1	1

第 1 次执行，选取最小标号度为 1 的点 3 和 Purfer Sequence 中的第 1 个数 1 连边：

将 1 和 3 的度分别减一：

顶点	1	2	3	4	5
度	1	3	0	1	1

第 2 次执行，选取最小标号度为 1 的点 1 和 Purfer Sequence 中的第 2 个数 2 连边：

将 1 和 2 的度分别减一：

顶点	1	2	3	4	5
度	0	2	0	1	1

第 3 次执行，将最小标号度为 1 的点 4 和 Purfer Sequence 第 3 个数 2 连边：

将 2 和 4 的度分别减一：

顶点	1	2	3	4	5
度	0	1	0	0	1

最后，还剩下两个点 2 和 5 的度为 1，连边：

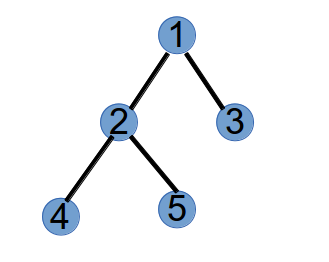
这样我们就知道，purfer序列必然与树是一一对应的。

而且我们还知道了一条性质，一个点在purfer序列中出现的次数等于其度数-1.

那我们来看一下这道题。

首先考虑无解的情况，这个很好判断，如果任意一个点的度数是0或者大于n-1那么就无解，否则有解。

之后再看一般的情况。我们假设一共有m个节点是有度数限制的，剩下n-m个节点没有度数限制。那么sum = sigma 1～m（d[i] - 1）

也就是说，这些点占据了purfer序列中sum个位置（一共有n-2个位置），所以这次选择的种类是C（n-2，sum）

之后对于这个长度为sum的序列，我们考虑一下，第一个位置可以填入d[1]-1个数，选择的方案为C（sum，d[1]-1）,那么在第二个位置可以填d[2]-1个数，选择的方案就是C（sum-（d[1]-1）,d[2]-1）。

这样推下去，可以得到总的排列数是：（偷一下图吧(^_^)）

之后，因为剩下的n-2-sum个位置，每个没有度数限制，所以可以随便填，那么就还有m^(n-2-sum)种情况。把两者相乘即为答案。

不过写高精度是不可能的。

我们可以对每个元素都进行质因数分解，开个桶记录一下每个数的出现次数，最后把他们乘起来就好。可以先行约去分子分母中相同的数。

不过最后一波把所有数乘起来还是要高精的……不过反正是高精乘低精，比较好写。

写题的时候还有个小插曲……质因数分解的时候，非常智障的写成了while(p)，结果导致出现了floating point exception ：8这么个错误（好像在Windows下是RE）

不管怎么说，以后要注意啊。

上一下代码。（这题其实很神奇因为不需要求puffer序列）

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cmath>
#include<queue>
#include<set>
#define rep(i,a,n) for(int i = a;i <= n;i++)
#define per(i,n,a) for(int i = n;i >= a;i--)
#define enter putchar('\n')
using namespace std;
const int M = ;
int n,len,a,sum,k,tot;
int t[],ans[M+],prime[M+];
bool np[M];
int read()
{
  int ans = ,op = ;
  char ch = getchar();
  while(ch < '' || ch > '')
  {
      if(ch == '-') op = -;
      ch = getchar();
  }
  while(ch >='' && ch <= '')
  {
      ans *= ;
      ans += ch - '';
      ch = getchar();
  }
  return ans * op;
}
void euler()
{
    rep(i,,n)
    {
    if(!np[i]) prime[++tot] = i;
    for(int j = ;i * prime[j] <= n;j++)
    {
        np[prime[j] * i] = ;
        if(!(i % prime[j])) break;
    }
    }
}
void C(int a,int b)
{
    rep(i,b+,a)
    {
    int p = i,d = ;
    while(p > )
    {
        while (!(p % prime[d])) ans[d]++,p /= prime[d];
        d++;
    }
    }
    rep(i,,a-b)
    {
    int p = i,d = ;
    while(p > )
    {
        while (!(p % prime[d])) ans[d]--,p /= prime[d];
        d++;
    }
    }
}
void calc()
{
    int d = ;
    while(sum > )
    {
    while (!(sum % prime[d])) ans[d] += len,sum /= prime[d];
    d++;
    }
}
int main()
{
    n = read();
    euler();
    len = n-;
    rep(i,,n)
    {
    a = read();
    if(!a || a >= n)
    {
        printf("");
        return ;
    }
    if(a == -)
    {
        sum++;
        continue;
    }
    a--,C(len,a),len -= a;
    }
    if(len) calc();
    t[] = ,k = ;
    rep(i,,)
    {
    while(ans[i])
    {
        ans[i]--;
        rep(j,,k) t[j] *= prime[i];
        rep(j,,k) if(t[j] >= ) t[j+] += t[j]/,t[j] %= ;
        while(t[k+]) k++,t[k+] += t[k] / ,t[k] %= ;
    }
    }
    per(i,k,) printf("%d",t[i]); enter;
    return ;
}