题解报告：hdu 2196 Computer（树形dp）

Problem Description

A school bought the first computer some time ago(so this computer's id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information. 

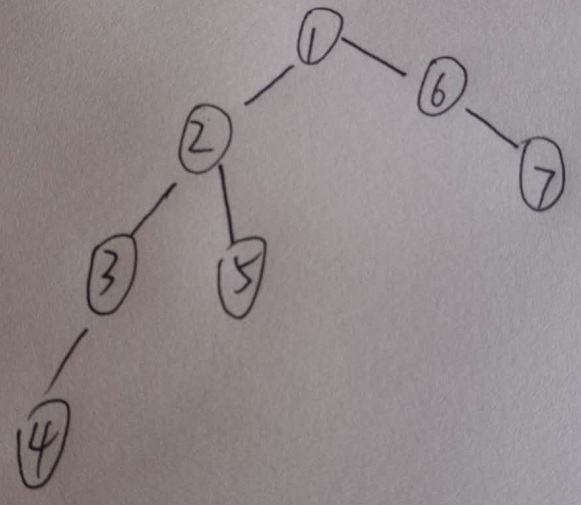
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

Input

Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.

Output

For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).

Sample Input

5

1 1

2 1

3 1

1 1

Sample Output

3

2

3

4

4

解题思路：求出树中每个节点能达到的最远距离。对于每个节点u来说，其可能到达的最长距离为max{其子树内的最长距离，其父节点不经过u的子树内的最长距离}。结合树的直径求法(1次dfs)便可得到最长链、每个节点的最长距离dp[u][0]和次长距离dp[u][1]。再一次dfs就是求节点u的反向最长距离即其父节点不经过u的子树内的最长距离dp[u][2]，有两种情况：①如果当前节点v不在树的直径上，那么dp[v][2]的值为max{其父节点u所在子树的最长距离dp[u][0]，其父节点u的父节点不经过u的子树内的最长距离即u的反向距离dp[u][2]}+dist(u,v)；例如5号节点，其dp[5][2]=max{dp[2][0],dp[2][2]}+1(2,5)=[5--2--1--6--7]=3+1=4。②如果当前节点v在树的直径上，那么dp[v][2]的值为max{其父节点u的反向最长距离dp[u][2]，其父节点的次长距离dp[u][1]}+dist(u,v)，例如3号节点，其dp[3][2]=max{dp[2][1],dp[2][2]}+1(2,3)=[3--2--1--6--7]=3+1=4。最后每个节点u能达到的最远距离就是max{正向最长距离dp[u][0]，反向最长距离dp[u][2]}。

AC代码(31ms)：

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn=;
 struct node{int to,next,len;}edge[maxn<<];
 int n,x,y,cnt,head[maxn],dp[maxn][],lgst[maxn];
 void add_edge(int u,int v,int w){
     edge[cnt].to=v;
     edge[cnt].len=w;
     edge[cnt].next=head[u];
     head[u]=cnt++;
 }
 int dfs1(int u,int fa){
     int Dmax=,Dsec=;
     for(int i=head[u];~i;i=edge[i].next){
         int v=edge[i].to;
         if(v^fa){
             int nowd=dfs1(v,u)+edge[i].len;
             if(nowd>Dmax)lgst[u]=v,Dsec=Dmax,Dmax=nowd;//lgst[u]=v记录u的正向最长路径上的节点v
             else if(nowd>Dsec)Dsec=nowd;
         }
     }
     dp[u][]=Dmax,dp[u][]=Dsec;//记录每个节点的正向最长距离和正向次长距离
     return Dmax;//返回正向最长距离
 }
 void dfs2(int u,int fa){
     for(int i=head[u];~i;i=edge[i].next){
         int v=edge[i].to;
         if(v^fa){
             if(v==lgst[u])dp[v][]=max(dp[u][],dp[u][])+edge[i].len;
             else dp[v][]=max(dp[u][],dp[u][])+edge[i].len;
             dfs2(v,u);
         }
     }
 }
 int main(){
     while(~scanf("%d",&n)){
         cnt=;memset(head,-,sizeof(head));
         memset(dp,,sizeof(dp));
         memset(lgst,,sizeof(lgst));
         for(int i=;i<=n;++i){
             scanf("%d%d",&x,&y);
             add_edge(i,x,y);
             add_edge(x,i,y);
         }
         dfs1(,-);
         dfs2(,-);
         for(int i=;i<=n;++i)
             printf("%d\n",max(dp[i][],dp[i][]));
     }
     return ;
 }