bzoj 1814: Ural 1519 Formula 1【插头dp】

设f[i][j][s]为轮廓线推到格子(i,j)，状态为s的方案数

括号表示一段线的左端和右端，表示成左括号和右括号，状压的时候用1和2表示，0表示已经闭合

下面的蓝线是黄色格子的轮廓线，dp转移要把它转到橙色轮廓线，设已经在状压的s中取到两条边的状态记为b1,b2



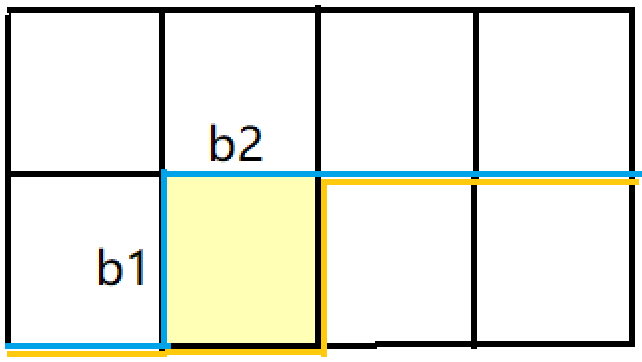
然后分很多情况讨论：

(i,j)是障碍：那就只能什么都不放的转移，也就是只能从b1=0,b2=0转移到新轮廓线的b1=0,b2=0

if(!a[i][j])
				{
					if(!b1&&!b2)
						add(x,v);
				}

b1=0,b2=0：因为不能空，所以只能转移一个拐角

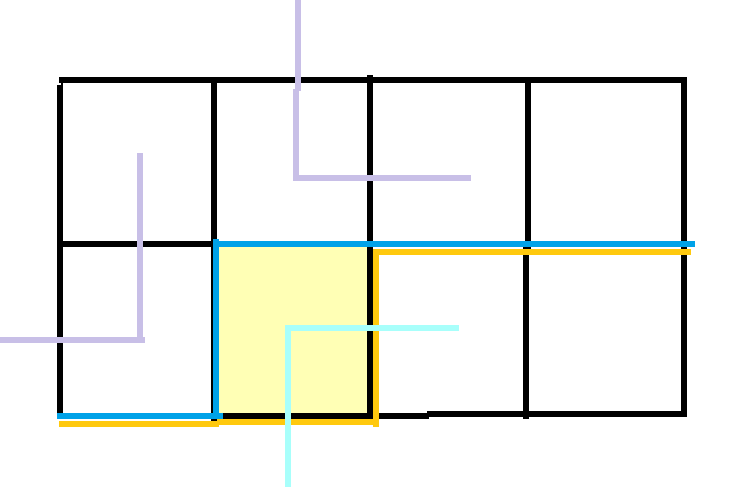
else if(!b1&&!b2)
				{
					if(a[i+1][j]&&a[i][j+1])
						add(x+b[j-1]+2*b[j],v);
				}

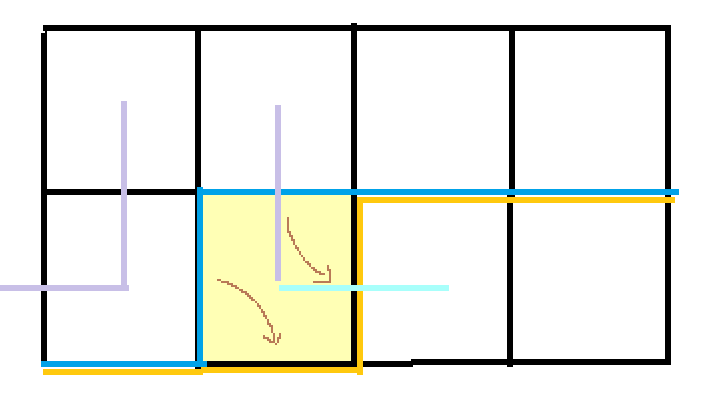
b1=0或者b2=0：根据有无障碍判断能不能转移，如果(i,j+1),(i+1,j)都没有障碍的话就有两种转移，以b1=0,b2!=0为例：

一种是接上然后拐弯，这样转移后的轮廓线括号状态不变



另一种是接上直着走，转移后的轮廓线括号状态b1b2互换



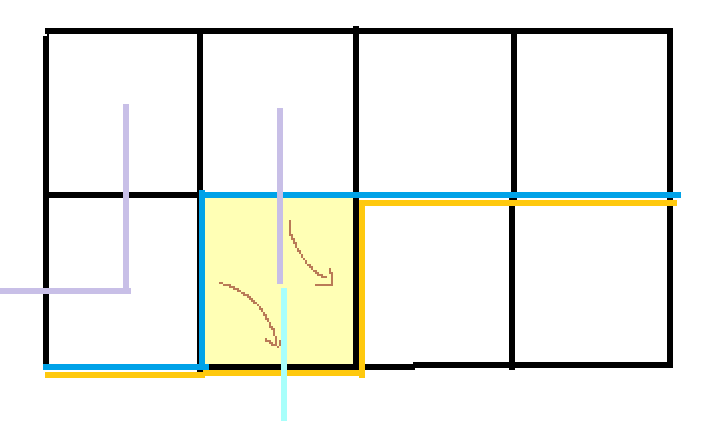
b1!=0,b2=0同理

else if(!b1&&b2)
				{
					if(a[i][j+1])
						add(x,v);
					if(a[i+1][j])
						add(x-b[j]*b2+b[j-1]*b2,v);
				}
				else if(b1&&!b2)
				{
					if(a[i][j+1])
						add(x-b[j-1]*b1+b[j]*b1,v);
					if(a[i+1][j])
						add(x,v);
				}

b1=b2=1或2：这样这两条线会在(i,j)格子连起来，两队括号合成一对，以b1=b2=1为例：

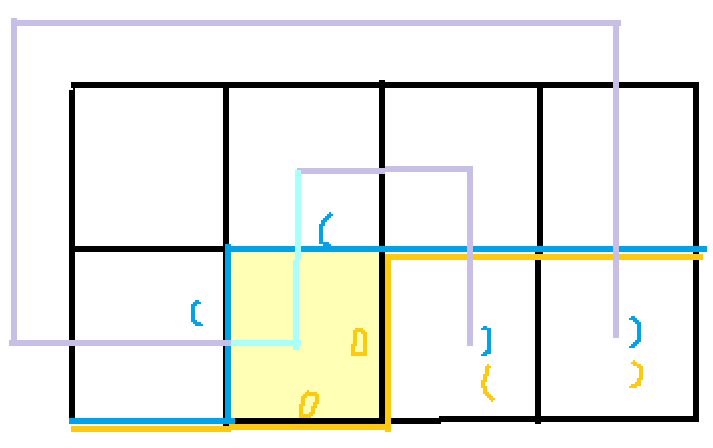
else if(b1==1&&b2==1)
				{
					for(int t=1,l=j+1;l<=m;l++)
					{
						if((x>>(l*2))%4==1)
							t++;
						if((x>>(l*2))%4==2)
							t--;
						if(!t)
						{
							add(x-b[j]-b[j-1]-b[l],v);
							break;
						}
					}
				}
				else if(b1==2&&b2==2)
				{
					for(int t=1,l=j-2;l>=0;l--)
					{
						if((x>>(l*2))%4==1)
							t--;
						if((x>>(l*2))%4==2)
							t++;
						if(!t)
						{
							add(x+b[l]-2*b[j]-2*b[j-1],v);
							break;
						}
					}
				}

b1=2,b2=1：和上面差不多，就是把这两个括号合并就行了

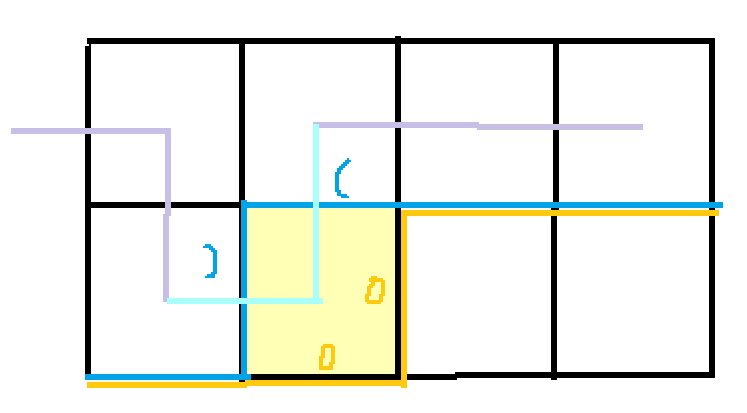
else if(b1==2&&b2==1)
					add(x-2*b[j-1]-b[j],v);

b1=1,b2=2：这个只有到最后一个没障碍的点才能转移，因为这是把一条线连成一个回路的最后一步

其实不用转移，直接加进答案就行了

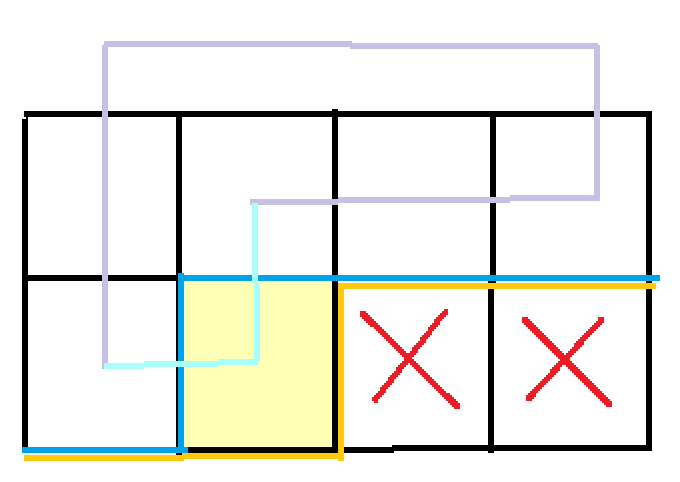
else if(i==tx&&j==ty)
					ans+=v;

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=15,mod=299989;
int n,m,la,nw,a[N][N],b[N],c[2],h[300005],tx,ty;
long long ans;
char s[N];
struct qwe
{
	int ne,to[2];
	long long va[2];
}e[300005];
void add(int x,long long v)
{
	int u=x%mod+1;
	for(int i=h[u];i;i=e[i].ne)
		if(e[i].to[nw]==x)
		{
			e[i].va[nw]+=v;
			return;
		}
	e[++c[nw]].ne=h[u];
	e[c[nw]].to[nw]=x;
	e[c[nw]].va[nw]=v;
	h[u]=c[nw];
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%s",s+1);
		for(int j=1;j<=m;j++)
			if(s[j]=='.')
				a[i][j]=1,tx=i,ty=j;
	}
	b[0]=1;
	for(int i=1;i<=12;i++)
		b[i]=b[i-1]<<2;
	c[0]=1,e[1].va[0]=1,e[1].to[0]=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=c[nw];j++)
			e[j].to[nw]<<=2;
		for(int j=1;j<=m;j++)
		{
			la=nw,nw^=1;
			memset(h,0,sizeof(h));
			c[nw]=0;
			for(int k=1;k<=c[la];k++)
			{
				int x=e[k].to[la],b1=(x>>(j*2-2))%4,b2=(x>>(j*2))%4;
				long long v=e[k].va[la];
				if(!a[i][j])
				{
					if(!b1&&!b2)
						add(x,v);
				}
				else if(!b1&&!b2)
				{
					if(a[i+1][j]&&a[i][j+1])
						add(x+b[j-1]+2*b[j],v);
				}
				else if(!b1&&b2)
				{
					if(a[i][j+1])
						add(x,v);
					if(a[i+1][j])
						add(x-b[j]*b2+b[j-1]*b2,v);
				}
				else if(b1&&!b2)
				{
					if(a[i][j+1])
						add(x-b[j-1]*b1+b[j]*b1,v);
					if(a[i+1][j])
						add(x,v);
				}
				else if(b1==1&&b2==1)
				{
					for(int t=1,l=j+1;l<=m;l++)
					{
						if((x>>(l*2))%4==1)
							t++;
						if((x>>(l*2))%4==2)
							t--;
						if(!t)
						{
							add(x-b[j]-b[j-1]-b[l],v);
							break;
						}
					}
				}
				else if(b1==2&&b2==2)
				{
					for(int t=1,l=j-2;l>=0;l--)
					{
						if((x>>(l*2))%4==1)
							t--;
						if((x>>(l*2))%4==2)
							t++;
						if(!t)
						{
							add(x+b[l]-2*b[j]-2*b[j-1],v);
							break;
						}
					}
				}
				else if(b1==2&&b2==1)
					add(x-2*b[j-1]-b[j],v);
				else if(i==tx&&j==ty)
					ans+=v;
			}
		}
	}
	printf("%lld\n",ans);
	return 0;
}