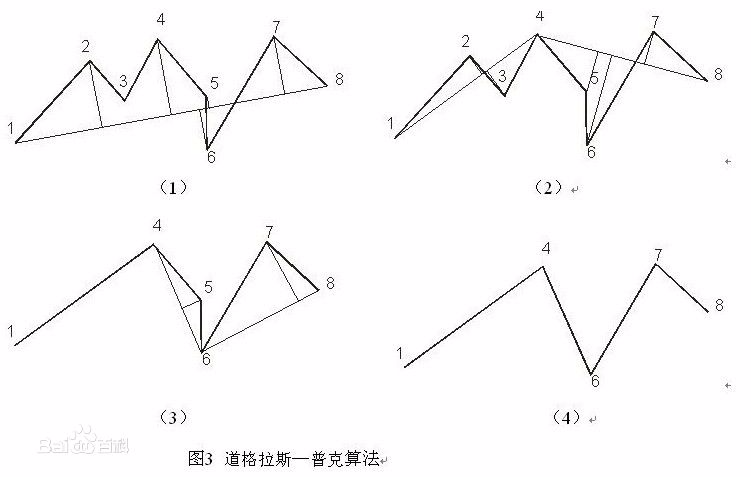
Douglas-Peucker 轨迹压缩算法
算法缺陷
对于一般路径而言,Douglas-Peucker算法是有效的,但是不难想到,当出现折返路径时,往外突出的部分很容易被压缩掉,因为偏差是以垂直距离为准的。下面的图片展示了这种情况下的压缩效果。 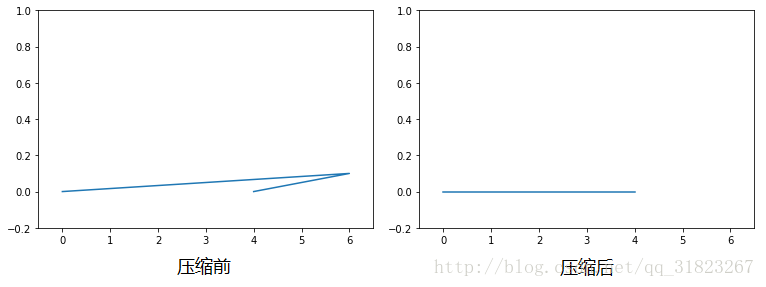
Douglas-Peucker 轨迹压缩算法的更多相关文章
- Douglas Peucker算法的C#实现
一.算法原理 Douglas-Peucker算法 在数字化过程中,需要对曲线进行采样简化,即在曲线上取有限个点,将其变为折线,并且能够在一定程度 上保持原有的形状. 经典的Douglas-Peucke ...
- 利用道格拉斯·普客法(DP法)压缩矢量多边形(C++)
1.算法描述 经典的Douglas-Peucker算法(简称DP法)描述如下: (1)在曲线首尾两点A,B之间连接一条直线AB,该直线为曲线的弦: (2)得到曲线上离该直线段距离最大的点C,计算其与A ...
- 盘点十大GIS相关算法
1.道格拉斯-普克算法(Douglas–Peucker) 道格拉斯-普克算法(Douglas–Peucker algorithm,亦称为拉默-道格拉斯-普克算法.迭代适应点算法.分裂与合并算法)是将曲 ...
- GIS原理学习目录
GIS原理学习目录 内容提要 本网络教程是教育部“新世纪网络课程建设工程”的实施课程.系统扼要地阐述地理信息系统的技术体系,重点突出地理信息系统的基本技术及方法. 本网络教程共分八章:第一章绪论,重点 ...
- OpenCV 学习笔记03 凸包convexHull、道格拉斯-普克算法Douglas-Peucker algorithm、approxPloyDP 函数
凸形状内部的任意两点的连线都应该在形状里面. 1 道格拉斯-普克算法 Douglas-Peucker algorithm 这个算法在其他文章中讲述的非常详细,此处就详细撰述. 下图是引用维基百科的.ε ...
- .net中使用 道格拉斯-普特 抽希轨迹点
Douglas一Peukcer算法由D.Douglas和T.Peueker于1973年提出,简称D一P算法,是目前公认的线状要素化简经典算法.现有的线化简算法中,有相当一部分都是在该算法基础上进行改进 ...
- ZIP压缩算法详细分析及解压实例解释
最近自己实现了一个ZIP压缩数据的解压程序,觉得有必要把ZIP压缩格式进行一下详细总结,数据压缩是一门通信原理和计算机科学都会涉及到的学科,在通信原理中,一般称为信源编码,在计算机科学里,一般称为数据 ...
- MATLAB中绘制质点轨迹动图并保存成GIF
工作需要在MATLAB中绘制质点轨迹并保存成GIF以便展示. 绘制质点轨迹动图可用comet和comet3命令,使用例子如下: t = 0:.01:2*pi;x = cos(2*t).*(cos(t) ...
- SQL Server 游标运用:鼠标轨迹字符串分割
一.本文所涉及的内容(Contents) 本文所涉及的内容(Contents) 背景(Contexts) 游标模板(Cursor Template) 鼠标轨迹字符串分割SQL脚本实现(SQL Code ...
随机推荐
- noj 2033 一页书的书 [ dp + 组合数 ]
传送门 一页书的书 时间限制(普通/Java) : 1000 MS/ 3000 MS 运行内存限制 : 65536 KByte总提交 : 53 测试通过 : 1 ...
- msp430入门编程17
msp430中C语言的寄存器操作 msp430入门学习 msp430入门编程
- vagrant的学习之Git学习
vagrant的学习之Git学习 参考学习网址: http://www.runoob.com/git/git-install-setup.html. http://www.bootcss.com/p/ ...
- python学习之-- importlib模块
importlib 模块 Python提供了importlib包作为标准库的一部分.目的就是提供Python中import语句的实现(以及__import__函数).另外,importlib允许程序员 ...
- Beat---hdu2614
http://acm.hdu.edu.cn/showproblem.php?pid=2614 题目大意 题目就不粘了 就是一个简单的深搜 由于我深搜实在是不懂 就在写一个博客记录一下 #in ...
- T1365 浴火银河星际跳跃 codevs
http://codevs.cn/problem/1365/ 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 黄金 Gold 题目描述 Description 小 K 又在玩浴 ...
- Java简单实验--关于课后提到的java重载函数的简单分析
根据这一小段代码,获得了以下的测试截图: 简单分析:根据输出结果,判断这段代码用到了两个不同的函数方法,输出的不止有double类型的数,还有整型的数. 又根据类中的定义情况,square是根据判断传 ...
- Linux进程IPC浅析[进程间通信SystemV共享内存]
Linux进程IPC浅析[进程间通信SystemV共享内存] 共享内存概念,概述 共享内存的相关函数 共享内存概念,概述: 共享内存区域是被多个进程共享的一部分物理内存 多个进程都可把该共享内存映射到 ...
- 深入浅出 - Android系统移植与平台开发(十二)- Android JNI机制
第五章.JNI机制 4.1 JNI概述 由前面基础知识可知,Android的应用层由Java语言编写,Framework框架层则是由Java代码与C/C++语言实现,之所以由两种不同的语言组合开发框架 ...
- 嵌入式开发之命令行---linux下的find文件查找命令与grep文件内容查找命令
在使用linux时,经常需要进行文件查找.其中查找的命令主要有find和grep.两个命令是有区的. 区别:(1)find命令是根据文件的属性进行查找,如文件名,文件大小,所有者,所属组,是否为空,访 ...
