浅析SkipList跳跃表原理及代码实现

本文将总结一种数据结构：跳跃表。前半部分跳跃表性质和操作的介绍直接摘自《让算法的效率跳起来--浅谈“跳跃表”的相关操作及其应用》上海市华东师范大学第二附属中学 魏冉。之后将附上跳跃表的源代码，以及本人对其的了解。难免有错误之处，希望指正，共同进步。谢谢。

跳跃表（Skip List）是1987年才诞生的一种崭新的数据结构，它在进行查找、插入、删除等操作时的期望时间复杂度均为O(logn),有着近乎替代平衡树的本领。而且最重要的一点，就是它的编程复杂度较同类的AVL树，红黑树等要低得多，这使得其无论是在理解还是在推广性上，都有着十分明显的优势。

首先，我们来看一下跳跃表的结构

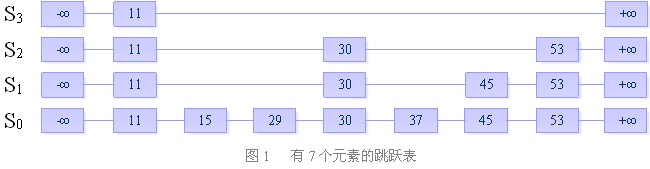
跳跃表由多条链构成（S0，S1，S2 ……，Sh），且满足如下三个条件：

每条链必须包含两个特殊元素：+∞ 和 -∞(其实不需要)
S0包含所有的元素，并且所有链中的元素按照升序排列。
每条链中的元素集合必须包含于序数较小的链的元素集合。
   操作

一、查找
   目的：在跳跃表中查找一个元素x
   在跳跃表中查找一个元素x，按照如下几个步骤进行：
      1. 从最上层的链（Sh）的开头开始
      2. 假设当前位置为p，它向右指向的节点为q（p与q不一定相邻），且q的值为y。将y与x作比较
          (1) x=y  输出查询成功及相关信息
          (2) x>y  从p向右移动到q的位置
          (3) x<y  从p向下移动一格

3. 如果当前位置在最底层的链中（S0），且还要往下移动的话，则输出查询失败

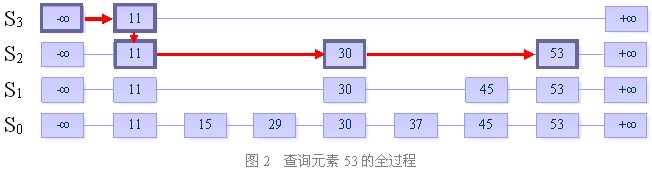
二、插入
     目的：向跳跃表中插入一个元素x
     首先明确，向跳跃表中插入一个元素，相当于在表中插入一列从S0中某一位置出发向上的连续一段元素。有两个参数需要确定，即插入列的位置以及它的“高度”。
     关于插入的位置，我们先利用跳跃表的查找功能，找到比x小的最大的数y。根据跳跃表中所有链均是递增序列的原则，x必然就插在y的后面。
     而插入列的“高度”较前者来说显得更加重要，也更加难以确定。由于它的不确定性，使得不同的决策可能会导致截然不同的算法效率。为了使插入数据之后，保持该数据结构进行各种操作均为O(logn)复杂度的性质，我们引入随机化算法（Randomized Algorithms）。

我们定义一个随机决策模块，它的大致内容如下：

产生一个0到1的随机数r     r ← random() 
如果r小于一个常数p，则执行方案A，  if  r<p then do A 
否则，执行方案B         else do B 
     初始时列高为1。插入元素时，不停地执行随机决策模块。如果要求执行的是A操作，则将列的高度加1，并且继续反复执行随机决策模块。直到第i次，模块要求执行的是B操作，我们结束决策，并向跳跃表中插入一个高度为i的列。

我们来看一个例子：
     假设当前我们要插入元素“40”，且在执行了随机决策模块后得到高度为4
     步骤一：找到表中比40小的最大的数，确定插入位置

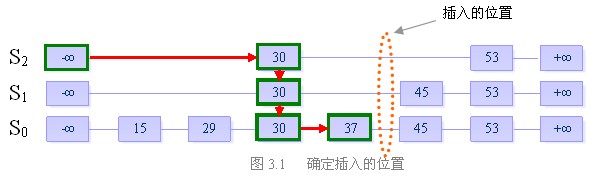
步骤二：插入高度为4的列，并维护跳跃表的结构

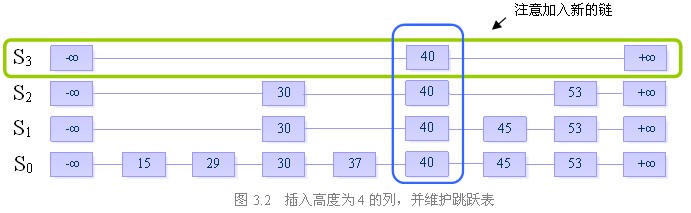
三、删除

目的：从跳跃表中删除一个元素x
    删除操作分为以下三个步骤：

在跳跃表中查找到这个元素的位置，如果未找到，则退出 
将该元素所在整列从表中删除 
将多余的“空链”删除

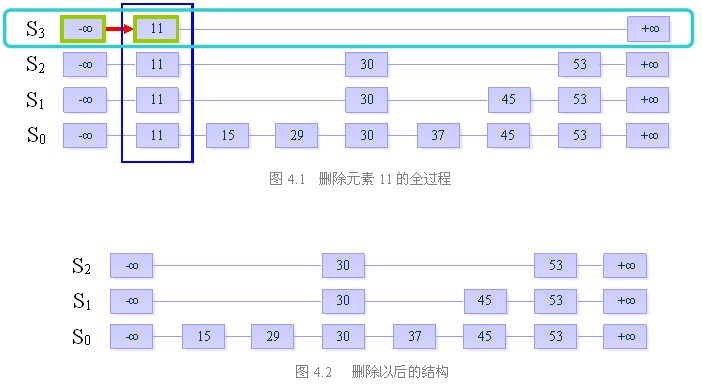
    我们来看一下跳跃表的相关复杂度：
 
       空间复杂度： O(n)       （期望）
       跳跃表高度： O(logn)  （期望）

相关操作的时间复杂度：
      查找：  O(logn)    （期望）
      插入：  O(logn)    （期望）
      删除：  O(logn)   （期望）
  
    之所以在每一项后面都加一个“期望”，是因为跳跃表的复杂度分析是基于概率论的。有可能会产生最坏情况，不过这种概率极其微小。

--------------------------------------------------------------------------------

以下是自己学习时碰到的一些问题

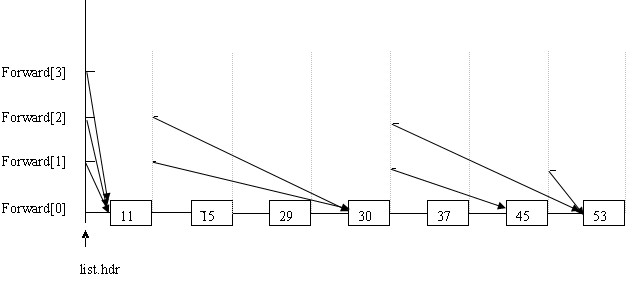
首先分配一个链表，用list.hdr指向，长度为跳跃表规定的最高层，说是链表，在以下代码中只是分配了一段连续的空间，用来指向每一层的开始位置。我们看到结构体nodeType中，有一个key,一个rec(用户数据)，还有一个指向结构体的指针数组。

一开始的那些图容易给人误解。如上图所示，例如每个节点的forward[2]，就认为是跳跃表的第3层。List.hdr的forward[2]指向11，11的forward[2]指向30，30的forward[2]指向53。这就是跳跃表的第3层：11---30-----53。（准确的说每个forward都指向新节点，新节点的同层forward又指向另一个节点，从而构成一个链表，而数据只有一个，并不是像开始途中所画的那样有N个副本）。本人天资愚钝，看了挺长时间才把它在内存里的结构看清楚了，呵呵。

SkipList在leveldb以及lucence中都广为使用，是比较高效的数据结构。由于它的代码以及原理实现的简单性，更为人们所接受。我们首先看看SkipList的定义，为什么叫跳跃表？

“     Skip lists  are data structures  that use probabilistic  balancing rather  than  strictly  enforced balancing. As a result, the algorithms  for insertion  and deletion in skip lists  are much simpler and significantly  faster  than  equivalent  algorithms  for balanced trees.   ”

译文：跳跃表使用概率均衡技术而不是使用强制性均衡，因此，对于插入和删除结点比传统上的平衡树算法更为简洁高效。

我们看一个图就能明白，什么是跳跃表，如图1所示：

图1：跳跃表简单示例

如上图所示，是一个即为简单的跳跃表。传统意义的单链表是一个线性结构，向有序的链表中插入一个节点需要O(n)的时间，查找操作需要O(n)的时间。如果我们使用图1所示的跳跃表，就可以减少查找所需时间为O(n/2)，因为我们可以先通过每个节点的最上面的指针先进行查找，这样子就能跳过一半的节点。比如我们想查找19，首先和6比较，大于6之后，在和9进行比较，然后在和12进行比较......最后比较到21的时候，发现21大于19，说明查找的点在17和21之间，从这个过程中，我们可以看出，查找的时候跳过了3、7、12等点，因此查找的复杂度为O(n/2)。查找的过程如下图2：

   图2：跳跃表查找操作简单示例

其实，上面基本上就是跳跃表的思想，每一个结点不单单只包含指向下一个结点的指针，可能包含很多个指向后续结点的指针，这样就可以跳过一些不必要的结点，从而加快查找、删除等操作。对于一个链表内每一个结点包含多少个指向后续元素的指针，这个过程是通过一个随机函数生成器得到，这样子就构成了一个跳跃表。这就是为什么论文“Skip Lists : A Probabilistic Alternative to Balanced Trees ”中有“概率”的原因了，就是通过随机生成一个结点中指向后续结点的指针数目。随机生成的跳跃表可能如下图3所示：

  图3：随机生成的跳跃表

跳跃表的大体原理，我们就讲述到这里。下面我们将从如下几个方面来探讨跳跃表的操作：

1、重要数据结构定义

2、初始化表

3、查找

4、插入

5、删除

6、随机数生成器

7、释放表

8、性能比较

（一）重要数据结构定义

从图3中，我们可以看出一个跳跃表是由结点组成，结点之间通过指针进行链接。因此我们定义如下数据结构：

//定义key和value的类型
typedef int KeyType;
typedef int ValueType;

//定义结点
typedef struct nodeStructure* Node;
struct nodeStructure{
    KeyType key;
    ValueType value;
    Node forward[];
};

//定义跳跃表
typedef struct listStructure* List;
struct listStructure{
    int level;
    Node header;
};

每一个结点都由3部分组成，key（关键字）、value（存放的值）以及forward数组（指向后续结点的数组，这里只保存了首地址）。通过这些结点，我们就可以创建跳跃表List，它是由两个元素构成，首结点以及level（当前跳跃表内最大的层数或者高度）。这样子，基本的数据结构定义完毕了。

（二）初始化表
     初始化表主要包括两个方面，首先就是header节点和NIL结点的申请，其次就是List资源的申请。

void SkipList::NewList(){
    //设置NIL结点
    NewNodeWithLevel(, NIL_);
    NIL_->key = 0x7fffffff;
    //设置链表List
    list_ = (List)malloc(sizeof(listStructure));
    list_->level = ;
    //设置头结点
    NewNodeWithLevel(MAX_LEVEL,list_->header);
    for(int i = ; i < MAX_LEVEL; ++i){
        list_->header->forward[i] = NIL_;
    }
    //设置链表元素的数目
    size_ = ;
}

void SkipList::NewNodeWithLevel(const int& level,
                                Node& node){
    //新结点空间大小
    int total_size = sizeof(nodeStructure) + level*sizeof(Node);
    //申请空间
    node = (Node)malloc(total_size);
    assert(node != NULL);
}

其中，NewNodeWithLevel是申请结点（总共level层）所需的内存空间。NIL_节点会在后续全部代码实现中可以看到。

（三）查找

查找就是给定一个key，查找这个key是否出现在跳跃表中，如果出现，则返回其值，如果不存在，则返回不存在。我们结合一个图就是讲解查找操作，如下图4所示：

图4：查找操作前的跳跃表

如果我们想查找19是否存在？如何查找呢？我们从头结点开始，首先和9进行判断，此时大于9，然后和21进行判断，小于21，此时这个值肯定在9结点和21结点之间，此时，我们和17进行判断，大于17，然后和21进行判断，小于21，此时肯定在17结点和21结点之间，此时和19进行判断，找到了。具体的示意图如图5所示：

图5：查找操作后的跳跃表

bool SkipList::Search(const KeyType& key,
                      ValueType& value){
    Node x = list_->header;
    int i;
    for(i = list_->level; i >= ; --i){
        while(x->forward[i]->key < key){
            x = x->forward[i];
        }
    }
    x = x->forward[];
    if(x->key == key){
        value = x->value;
        return true;
    }else{
        return false;
    }
}

（四）插入

插入包含如下几个操作：1、查找到需要插入的位置   2、申请新的结点    3、调整指针。

我们结合下图6进行讲解，查找如下图的灰色的线所示  申请新的结点如17结点所示， 调整指向新结点17的指针以及17结点指向后续结点的指针。这里有一个小技巧，就是使用update数组保存大于17结点的位置，这样如果插入17结点的话，就指针调整update数组和17结点的指针、17结点和update数组指向的结点的指针。update数组的内容如红线所示，这些位置才是有可能更新指针的位置。

  图6：插入操作示意图（感谢博主：来自cnblogs的qiang.xu ）

bool SkipList::Insert(const KeyType& key,
                      const ValueType& value){
    Node update[MAX_LEVEL];
    int i;
    Node x = list_->header;
    //寻找key所要插入的位置
    //保存大于key的位置信息
    for(i = list_->level; i >= ; --i){
        while(x->forward[i]->key < key){
            x = x->forward[i];
        }

        update[i] = x;
    }

    x = x->forward[];
    //如果key已经存在
    if(x->key == key){
        x->value = value;
        return false;
    }else{
        //随机生成新结点的层数
        int level = RandomLevel();
        //为了节省空间，采用比当前最大层数加1的策略
        if(level > list_->level){
            level = ++list_->level;
            update[level] = list_->header;
        }
        //申请新的结点
        Node newNode;
        NewNodeWithLevel(level, newNode);
        newNode->key = key;
        newNode->value = value;

        //调整forward指针
        for(int i = level; i >= ; --i){
            x = update[i];
            newNode->forward[i] = x->forward[i];
            x->forward[i] = newNode;
        }

        //更新元素数目
        ++size_;

        return true;
    }
}

（五）删除

删除操作类似于插入操作，包含如下3步：1、查找到需要删除的结点 2、删除结点  3、调整指针

图7：删除操作示意图（感谢博主qiang.xu 来自cnblogs）

bool SkipList::Delete(const KeyType& key,
                      ValueType& value){
    Node update[MAX_LEVEL];
    int i;
    Node x = list_->header;
    //寻找要删除的结点
    for(i = list_->level; i >= ; --i){
        while(x->forward[i]->key < key){
            x = x->forward[i];
        }

        update[i] = x;
    }

    x = x->forward[];
    //结点不存在
    if(x->key != key){
        return false;
    }else{
        value = x->value;
        //调整指针
        for(i = ; i <= list_->level; ++i){
            if(update[i]->forward[i] != x)
                break;
            update[i]->forward[i] = x->forward[i];
        }
        //删除结点
        free(x);
        //更新level的值，有可能会变化，造成空间的浪费
        while(list_->level >
            && list_->header->forward[list_->level] == NIL_){
            --list_->level;
        }

        //更新链表元素数目
        --size_;

        return true;
    }
}

（六）随机数生成器

再向跳跃表中插入新的结点时候，我们需要生成该结点的层数，使用的就是随机数生成器，随机的生成一个层数。这部分严格意义上讲，不属于跳跃表的一部分。随机数生成器说简单很简单，说难很也很难，看你究竟是否想生成随机的数。可以采用c语言中srand以及rand函数，也可以自己设计随机数生成器。

此部分我们采用levelDB随机数生成器：

// Copyright (c) 2011 The LevelDB Authors. All rights reserved.
// Use of this source code is governed by a BSD-style license that can be
// found in the LICENSE file. See the AUTHORS file for names of contributors.

#include <stdint.h>

//typedef unsigned int           uint32_t;
//typedef unsigned long long     uint64_t;

// A very simple random number generator.  Not especially good at
// generating truly random bits, but good enough for our needs in this
// package.
class Random {
 private:
  uint32_t seed_;
 public:
  explicit Random(uint32_t s) : seed_(s & 0x7fffffffu) {
    // Avoid bad seeds.
    if (seed_ ==  || seed_ == 2147483647L) {
      seed_ = ;
    }
  }
  uint32_t Next() {
    static const uint32_t M = 2147483647L;   // 2^31-1
    static const uint64_t A = ;  // bits 14, 8, 7, 5, 2, 1, 0
    // We are computing
    //       seed_ = (seed_ * A) % M,    where M = 2^31-1
    //
    // seed_ must not be zero or M, or else all subsequent computed values
    // will be zero or M respectively.  For all other values, seed_ will end
    // up cycling through every number in [1,M-1]
    uint64_t product = seed_ * A;

    // Compute (product % M) using the fact that ((x << 31) % M) == x.
    seed_ = static_cast<uint32_t>((product >> ) + (product & M));
    // The first reduction may overflow by 1 bit, so we may need to
    // repeat.  mod == M is not possible; using > allows the faster
    // sign-bit-based test.
    if (seed_ > M) {
      seed_ -= M;
    }
    return seed_;
  }
  // Returns a uniformly distributed value in the range [0..n-1]
  // REQUIRES: n > 0
  uint32_t Uniform(int n) { return (Next() % n); }

  // Randomly returns true ~"1/n" of the time, and false otherwise.
  // REQUIRES: n > 0
  bool OneIn(int n) { return (Next() % n) == ; }

  // Skewed: pick "base" uniformly from range [0,max_log] and then
  // return "base" random bits.  The effect is to pick a number in the
  // range [0,2^max_log-1] with exponential bias towards smaller numbers.
  uint32_t Skewed(int max_log) {
    return Uniform( << Uniform(max_log + ));
  }
};

其中核心的是 seed_ = (seed_ * A) % M这个函数，并且调用一次就重新更新一个种子seed。以达到随机性。

根据个人喜好，自己可以独立设计随机数生成器，只要能够返回一个随机的数字即可。

（七）释放表

释放表的操作比较简单，只要像单链表一样释放表就可以，释放表的示意图8如下：

      图8：释放表

void SkipList::FreeList(){
    Node p = list_->header;
    Node q;
    while(p != NIL_){
        q = p->forward[];
        free(p);
        p = q;
    }
    free(p);
    free(list_);
}

（八）性能比较

我们对跳跃表、平衡树等进行比较，如下图9所示：

  图9：性能比较图

从中可以看出，随机跳跃表表现性能很不错，节省了大量复杂的调节平衡树的代码。