linux makefle学习

学习材料取之这个网址：http://blog.chinaunix.net/uid-27717694-id-3696246.html

学习环境：ubuntu10.04-64bit-desktop版，gcc-4.4.3

实际操作时考虑到方便性采用：Cygwin Terminal + source Insight3.5学习

首先贴上Makefile文件

edit : main.o kbd.o command.o display.o insert.o search.o files.o utils.o

    cc -o edit main.o kbd.o command.o display.o insert.o search.o files.o utils.o

main.o : main.c defs.h

    cc -c main.c

kbd.o : kbd.c defs.h command.h

    cc -c kbd.c

command.o : command.c defs.h command.h

    cc -c command.c

display.o : display.c defs.h buffer.h

    cc -c display.c

insert.o : insert.c defs.h buffer.h

    cc -c insert.c

search.o : search.c defs.h buffer.h

    cc -c search.c

files.o : files.c defs.h buffer.h command.h

    cc -c files.c

utils.o : utils.c defs.h

    cc -c utils.c

clean :

    rm edit main.o kbd.o command.o display.o insert.o search.o files.o utils.o

.csharpcode, .csharpcode pre
{
font-size: small;
color: black;
font-family: consolas, "Courier New", courier, monospace;
background-color: #ffffff;
/*white-space: pre;*/
}
.csharpcode pre { margin: 0em; }
.csharpcode .rem { color: #008000; }
.csharpcode .kwrd { color: #0000ff; }
.csharpcode .str { color: #006080; }
.csharpcode .op { color: #0000c0; }
.csharpcode .preproc { color: #cc6633; }
.csharpcode .asp { background-color: #ffff00; }
.csharpcode .html { color: #800000; }
.csharpcode .attr { color: #ff0000; }
.csharpcode .alt
{
background-color: #f4f4f4;
width: 100%;
margin: 0em;
}
.csharpcode .lnum { color: #606060; }

 

 

上来报“gcc 和makefile 以及Makefile:2: *** 遗漏分隔符 。 停止”错误，到网上一查，原来所有的命令前都需要加上一个tab空格，重新修改之，回到工程目录下，键入make再运行，成功，如下截图：

 

发现系统中生成了一个edit.exe文件，键入edit.exe再运行，结果报如下错误：

 

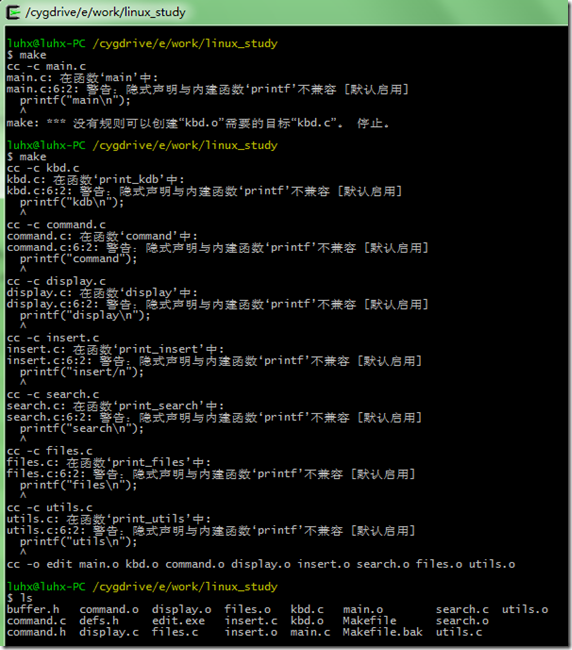
如果直接a.out，系统会在path路径下寻找该程序，如果找不到就会出command not found，运行自己的程序可以在该程序前加上该程序的绝对路径，但一般如果在该文件所在目录可以用./a.out运行

将当前路径加入PATH目录中即可，我的路径为：

/cygdrive/e/work/linux_study （通过pwd命令可查看）

则通过命令

vi ~/.bash_profile   修改PATH

打开文件，加入这行代码： #PATH=$PATH:/cygdrive/e/work/linux_study

然后狂按ESC键，按:w,再按:q保存修改，关闭cygwin,再次找开，进入之前运行的目录/cygdrive/e/work/linux_study,输入edit.exe，成功

截图如下：