HDU 5912 Fraction（模拟——分子式化简求解）

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=5912

Problem Description

Mr. Frog recently studied how to add two fractions up, and he came up with an evil idea to trouble you by asking you to calculate the result of the formula below:

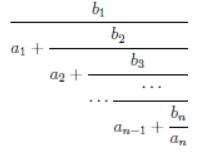
As a talent, can you figure out the answer correctly?

 

Input

The first line contains only one integer T, which indicates the number of test cases.

For each test case, the first line contains only one integer n (n≤8).

The second line contains n integers: a1,a2,⋯an(1≤ai≤10).
The third line contains n integers: b1,b2,⋯,bn(1≤bi≤10).

 

Output

For each case, print a line “Case #x: p q”, where x is the case number (starting from 1) and p/q indicates the answer.

You should promise that p/q is irreducible.

 

Sample Input

1

2

1 1

2 3

 

Sample Output

Case #1: 1 2

Hint

Here are the details for the first sample:
2/(1+3/1) = 1/2

 

Source

2016中国大学生程序设计竞赛（长春）-重现赛

题意描述：

给出上述图中的分子式，给出ai和bi

计算该分子形式的最简结果

解题思路：

总体来说还是比较考验数学思维的。

简单实用代入法看一下，例如只有a1，a2和b1，b2，那么结果可以写成b1/(a1+b2/a2)

初始是fz（分子）=b2，fm=a2，经过化简可得结果为b1*fm/(a1*fm+fz)，容易得到fz += fm*a[i];和fm *= b[i];只不过fz和fm需要交换一下（仔细验算一下）。

代码实现：

 #include<stdio.h>
 #include<algorithm>
 using namespace std;
 int gcd(int a,int b)
 {
     return b==? a : gcd(b,a%b);
 }
 int main()
 {
     int T,t=,n,i,a[],b[],k;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&n);
         for(i=;i<=n;i++) scanf("%d",&a[i]);
         for(i=;i<=n;i++) scanf("%d",&b[i]);
         int fz=b[n],fm=a[n];
         for(i=n-;i>=;i--)
         {
             fz += fm*a[i];
             fm *= b[i];
             swap(fz,fm);
         }
         k=gcd(fz,fm);
         printf("Case #%d: %d %d\n",t++,fz/k,fm/k);
     }
     return ;
  }