[Bayesian] “我是bayesian我怕谁”系列 - Latent Variables

下一章有意讲讲EM和变分推断的内容。

EM和变分推断的内容能Google到很多，虽然质量乘次不齐，但本文也无意再赘述那么些个细节。

此处记录一些核心思想，帮助菜鸡形成整体上的认识。不过，变分推断也不是一篇博文能讲述通透的技术，希望读者读完此文，至少知道自己将要学一个什么好东西，能用它来做什么。

私以为，变分的理解就是统计机器学习的核心，那么，

• 不懂变分怎么能说学会了统计机器学习？  P(统计机器学习 | 变分)
• 不会统计机器学习怎么自诩会机器学习？  P(机器学习 | 统计机器学习)
• 不懂机器学习如何有资格研究深度学习？  P(深度学习 | 机器学习)
• 不懂深度学习又怎么能从事人工智能呢？  P(人工智能 | 深度学习)
• 求边缘条件概率分布：P(人工智能 | 变分=False) = ?

但在此之前，需要提提Latent Variables隐变量。

隐变量，潜在的隐藏的变量，这个东西非常好，同时也能启迪你一些人生哲学。

“若能肯定自己，需要之前有一段否定自己的过程。“

看到的，即使看似合理也要抱着怀疑自己的态度，寻求背后的真实状态，比如hmm。

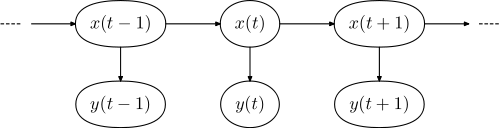
hmm PGM

看到了表象y，y之间貌似相关性也很强，但就是要先怀疑自己，反问：是否有”幕后黑手x“控制着整个局面？

然后，假设了隐变量以及之间的概率关系，剩下的问题就是如何求解概率关系的过程，即各个边（条件概率分布）咯。

因为要用到隐变量，所以更需要概率图来给读者以直观的感受，不同场景不同模型中的隐变量设计又有很多的共性，概率图中对这些共性的研究也可以形成一种”定理”类似的东西，发现某个新问题的概率图有某种共性出现，直接使用对应的性质即可，而不是重新造轮子。

有菜鸡问了，加那么多隐变量，边自然就多了，也就是需要估计的概率关系（变量）多了，自找麻烦么？

麻烦确实不少，所以不能加太多，但也有变态的事情，比如头几年的日本学界，据说有人在模型中加了二十多个圈圈，然后论文就容易发表了。（不可考证，笑笑即可）

变分推断就是估参的一个利器，既然是估计参数，就不必在精度上斤斤计较，渐进就好，当然”逼近真实“，“逼近的程度”也是一门艺术，更是技术。提到渐进，也就是常说的”优化“，其实机器学习整个领域都充斥着优化方法，你说不学“优化理论”能混下去么？

菜鸡菜鸡，不学习《多元变量分析》、《优化》，如何登榜提名，好发愁。

哎，到处都是潜规则。

还有一个原因，隐变量都是自己设计的，当然要设计一个友好的，隐变量间关系比较强，容易计算，且相对通用的结构。

而变分推断中假设了一些友好的分布来尽可能的逼近实际分布，在这个逼近的过程中，当然希望承载在一个相对友好的变量关系上面。

如此看来，似乎明了了许多。

变分推断的目的是逼近真实分布，mcmc采样方法也是同样的目的，二者选其一皆可。

至于两者的优劣，可以百度之，内容都烂大街咯。

EM可以理解为变分推断的一种狭义情况，好比二项分布是狭义的多项分布。

说到底， Latent Variables真没什么，多几个圈圈又能如何。

最近，cmu的Machine Learning 10-702刷屏，互联网带来的教育共享就是好啊，好东西就在网上，你能嗅得到么？让我们瞧上一瞧。

Schedule

Here is the estimated class schedule. It is subject to change, depending on time and class interests.

Tues Jan 17	L	Linear regression	Notes, video
Thurs Jan 19	L	Linear classification	Notes, video, cool plot
Tues Jan 24	R	Nonparametric regression	Notes, video
Thurs Jan 26	R	Nonparametric regression	Notes, video
Tues Jan 31	R	Nonparametric regression	Notes, video
Thurs Feb 2	R	Nonparametric classification	Notes, video	Hw 1 due Fri Feb 3
Tues Feb 7	L	Reproducing kernel Hilbert spaces	Notes, video
Thurs Feb 9	L	Density estimation	Notes, video
Tues Feb 14	L	Clustering	Notes, video
Thurs Feb 16	L	Clustering	Notes, video	Project milestone 1 due Fri Feb 17
Tues Feb 21	L	Clustering	Notes, video
Thurs Feb 23	L	High-dimensional testing	Notes, video
Tues Feb 28	L	Concentration of measure	Notes, video
Thurs Mar 2	L	Concentration of measure	Notes, video	Hw 2 due Fri Mar 3
Tues Mar 7	-	Midterm
Thurs Mar 9	-	Spring break (no class)
Tues Mar 14	-	Spring break (no class)
Thurs Mar 16	-	Spring break (no class)
Tues Mar 21	L	Minimax theory	Notes, video
Thurs Mar 23	L	Minimax theory	Notes, video
Tues Mar 28	R	Sparsity and the lasso	Notes, video
Thurs Mar 30	R	Sparsity and the lasso	Notes, video	Hw 3 due Mon Apr 3
Tues Apr 4	R	Sparsity and the lasso	Notes, video
Thurs Apr 6	R	Sparsity and the lasso	Notes, video	Project milestone 2 due Mon Apr 10
Tues Apr 11	L	Graphical models	Notes, video
Thurs Apr 13	L	Graphical models	Notes, video
Tues Apr 18	L	Advanced topic	Lei, Robins, and Wasserman, and Lei and Wasserman
Thurs Apr 20	-	Spring Carnival (no class)
Tues Apr 25	R	Advanced topic	Lei, Robins, and Wasserman, and Lei and Wasserman	Hw 4 due Wed Apr 26
Thurs Apr 27	R	Advanced topic	Lee, Sun, Sun, and Taylor, and Tibs, Taylor, Lockhart, and Tibs
Tues May 2	-	Course conference	Slides
Thurs May 4	-	Course conference	Slides	Project writeup due Fri May 5

从大纲看去，跟我的计划内容大有区别。在此就顺便再报一个潜规则。

如果你是数学系的同学，对数据分析感兴趣，学成之后，千万不要在计算机系的同学面前自夸数据分析；搞数据分析（机器学习）的计算机的同学们也不要在数学系面前卖弄算法。

很可能，很可能，很可能。。。　你们争辩的不是一个东西，但名字却都叫“统计学习”或者相关的名字。

不要纠结我的说法，自个儿瞧瞧各大院校统计学习课程的大纲，然后对比，玩味。

那么问题来了，为什么会如此？

数学系做数据分析很正常，往往从Linear regression，Linear classification这些考验数学基础的地方入手，如cmu的这份教学大纲。

统计机器学习内部也有派别，一派的代表就是prml，似乎更强调工程实践性，下图左；另一派的代表就是小黄书《The Elements of Statistical Learning》，下图右。

　　　左, prml;                 　右, little yellow book

当然了，到底学习的是哪个派别跟课程设在cse or math没有太多相关，主要还是看讲课教授的品味。

• 不要问我学哪一本比较好，我觉得都学了比较好。
• 不要问我哪一本更有优势，正妹从哪个角度看都是正妹。

正所谓知己知彼百战不殆，你若有心干掉数学系出身的竞争对手，建议“深入敌后，趁其课，学其书，使其优势化为乌有”。

这也是交叉学科领域的生存之道。

最后，cmu的课程设计更偏重数学修炼，这也是名校的潜规则。