源码分析 Large-Margin Softmax Loss for Convolutional Neural Networks
作者在Caffe中引入了一个新层,一般情况在Caffe中引入一个新层需要修改caffe.proto,添加该层头文件*.hpp,CPU实现*.cpp,GPU实现*.cu,代码结果如下图所示:

- caffe.proto
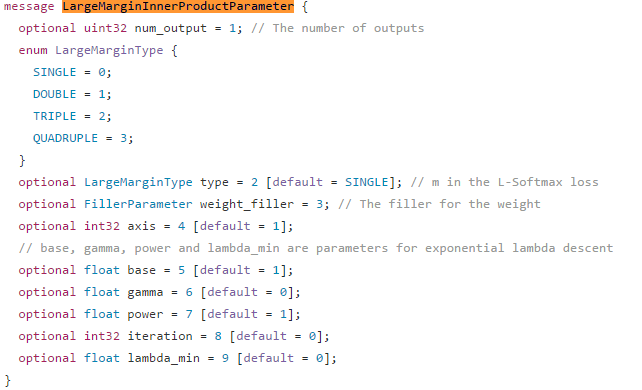
作者在caffe.proto中引入了largemargin_inner_product_laye层所需要的一些参数,例如num_output、type等,请注意一些参数有默认取值。
- largemargin_inner_product_laye.hpp
#ifndef CAFFE_LARGEMARGIN_INNER_PRODUCT_LAYER_HPP_
#define CAFFE_LARGEMARGIN_INNER_PRODUCT_LAYER_HPP_ #include <vector> #include "caffe/blob.hpp"
#include "caffe/layer.hpp"
#include "caffe/proto/caffe.pb.h" namespace caffe { /**
* @brief Also known as a "LargeMargin fully-connected" layer, computes an LargeMargin inner product
* with a set of learned weights, and (optionally) adds biases.
*
* TODO(dox): thorough documentation for Forward, Backward, and proto params.
*/
template <typename Dtype>
class LargeMarginInnerProductLayer : public Layer<Dtype> {
public:
explicit LargeMarginInnerProductLayer(const LayerParameter& param)
: Layer<Dtype>(param) {}
virtual void LayerSetUp(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Reshape(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top); virtual inline const char* type() const { return "LargeMarginInnerProduct"; }
virtual inline int ExactNumBottomBlobs() const { return ; }
virtual inline int MaxTopBlobs() const { return ; } protected:
virtual void Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Forward_gpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top);
virtual void Backward_cpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom);
virtual void Backward_gpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom); int M_;
int K_;
int N_; LargeMarginInnerProductParameter_LargeMarginType type_; // common variables
Blob<Dtype> x_norm_;
Blob<Dtype> w_norm_;
Blob<Dtype> cos_theta_;
Blob<Dtype> sign_0_; // sign_0 = sign(cos_theta)
// for DOUBLE type
Blob<Dtype> cos_theta_quadratic_;
// for TRIPLE type
Blob<Dtype> sign_1_; // sign_1 = sign(abs(cos_theta) - 0.5)
Blob<Dtype> sign_2_; // sign_2 = sign_0 * (1 + sign_1) - 2
Blob<Dtype> cos_theta_cubic_;
// for QUADRA type
Blob<Dtype> sign_3_; // sign_3 = sign_0 * sign(2 * cos_theta_quadratic_ - 1)
Blob<Dtype> sign_4_; // sign_4 = 2 * sign_0 + sign_3 - 3
Blob<Dtype> cos_theta_quartic_; int iter_;
Dtype lambda_; }; } // namespace caffe #endif // CAFFE_LARGEMARGIN_INNER_PRODUCT_LAYER_HPP_
作者在该头文件中遵循了“在caffe引入层的一般规范”,此外引入了一些变量。一些变量更具其命名,我们是可以大致猜出去含义的,如x_norm_,w_norm_。
- largemargin_inner_product_laye.cpp
由于该部分代码较多,因此笔者采取函数注释的方式进行分析(只要分析type=DOUBLE的情形)
#include <vector> #include "caffe/blob.hpp"
#include "caffe/common.hpp"
#include "caffe/filler.hpp"
#include "caffe/layer.hpp"
#include "caffe/util/math_functions.hpp"
#include "caffe/layers/largemargin_inner_product_layer.hpp" namespace caffe {
//该函数主要完成参数赋值、weight Blob初始化
template <typename Dtype>
void LargeMarginInnerProductLayer<Dtype>::LayerSetUp(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
CHECK_EQ(bottom[]->num(), bottom[]->num())
<< "Number of labels must match number of output; "
<< "DO NOT support multi-label this version."
<< "e.g., if prediction shape is (M X N), "
<< "label count (number of labels) must be M, "
<< "with integer values in {0, 1, ..., N-1}."; type_ = this->layer_param_.largemargin_inner_product_param().type();
iter_ = this->layer_param_.largemargin_inner_product_param().iteration();
lambda_ = (Dtype).; const int num_output = this->layer_param_.largemargin_inner_product_param().num_output();
N_ = num_output;
const int axis = bottom[]->CanonicalAxisIndex(
this->layer_param_.largemargin_inner_product_param().axis()); K_ = bottom[]->count(axis);
// Check if we need to set up the weights
if (this->blobs_.size() > ) {
LOG(INFO) << "Skipping parameter initialization";
} else {
this->blobs_.resize();
// Intialize the weight
vector<int> weight_shape();
weight_shape[] = N_;
weight_shape[] = K_;
this->blobs_[].reset(new Blob<Dtype>(weight_shape));//weight维度为(N_,K_)
// fill the weights
shared_ptr<Filler<Dtype> > weight_filler(GetFiller<Dtype>(
this->layer_param_.largemargin_inner_product_param().weight_filler()));
weight_filler->Fill(this->blobs_[].get());
} // parameter initialization
this->param_propagate_down_.resize(this->blobs_.size(), true);//weight大小设置以及初始化
} template <typename Dtype>
void LargeMarginInnerProductLayer<Dtype>::Reshape(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
// Figure out the dimensions
const int axis = bottom[]->CanonicalAxisIndex(
this->layer_param_.largemargin_inner_product_param().axis());
const int new_K = bottom[]->count(axis);
CHECK_EQ(K_, new_K)
<< "Input size incompatible with inner product parameters."; M_ = bottom[]->count(, axis);//单个样本输出维度N_,样本数M_,单个样本维度K_,请记住这三个参数的含义 vector<int> top_shape = bottom[]->shape();
top_shape.resize(axis + );
top_shape[axis] = N_;
top[]->Reshape(top_shape);//top的维度(M_,N_) // if needed, reshape top[1] to output lambda
vector<int> lambda_shape(, );
top[]->Reshape(lambda_shape);//为了加速收敛引入了指数退化项lambda // common variables
vector<int> shape_1_X_M(, M_);
x_norm_.Reshape(shape_1_X_M);//norm{xi},i属于[0,M_-1]
vector<int> shape_1_X_N(, N_);
w_norm_.Reshape(shape_1_X_N);//norm{wi},i属于[0,N_-1] sign_0_.Reshape(top_shape);
cos_theta_.Reshape(top_shape);//cos(theta)的维度(M_,N_) // optional temp variables
switch (type_) {
case LargeMarginInnerProductParameter_LargeMarginType_SINGLE:
break;
case LargeMarginInnerProductParameter_LargeMarginType_DOUBLE:
cos_theta_quadratic_.Reshape(top_shape);//cos(theta)^2的维度(M_,N_)
break;
case LargeMarginInnerProductParameter_LargeMarginType_TRIPLE:
cos_theta_quadratic_.Reshape(top_shape);
cos_theta_cubic_.Reshape(top_shape);
sign_1_.Reshape(top_shape);
sign_2_.Reshape(top_shape);
break;
case LargeMarginInnerProductParameter_LargeMarginType_QUADRUPLE:
cos_theta_quadratic_.Reshape(top_shape);
cos_theta_cubic_.Reshape(top_shape);
cos_theta_quartic_.Reshape(top_shape);
sign_3_.Reshape(top_shape);
sign_4_.Reshape(top_shape);
break;
default:
LOG(FATAL) << "Unknown L-Softmax type.";
}
} template <typename Dtype>
void LargeMarginInnerProductLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
iter_ += (Dtype).;
Dtype base_ = this->layer_param_.largemargin_inner_product_param().base();
Dtype gamma_ = this->layer_param_.largemargin_inner_product_param().gamma();
Dtype power_ = this->layer_param_.largemargin_inner_product_param().power();
Dtype lambda_min_ = this->layer_param_.largemargin_inner_product_param().lambda_min();
lambda_ = base_ * pow(((Dtype). + gamma_ * iter_), -power_);
lambda_ = std::max(lambda_, lambda_min_);
top[]->mutable_cpu_data()[] = lambda_;//指数退化项,iter_很大时,lambda_趋于0 /************************* common variables *************************/
const Dtype* bottom_data = bottom[]->cpu_data();
Dtype* mutable_x_norm_data = x_norm_.mutable_cpu_data();
for (int i = ; i < M_; i++) {
mutable_x_norm_data[i] = sqrt(caffe_cpu_dot(K_, bottom_data + i * K_, bottom_data + i * K_));//norm{xi}计算,i属于M_
}
const Dtype* weight = this->blobs_[]->cpu_data();
Dtype* mutable_w_norm_data = w_norm_.mutable_cpu_data();
for (int i = ; i < N_; i++) {
mutable_w_norm_data[i] = sqrt(caffe_cpu_dot(K_, weight + i * K_, weight + i * K_));//norm{wi}计算,i属于N_
} Blob<Dtype> xw_norm_product_;
xw_norm_product_.Reshape(cos_theta_.shape());
caffe_cpu_gemm<Dtype>(CblasTrans, CblasNoTrans, M_, N_, , (Dtype).,
x_norm_.cpu_data(), w_norm_.cpu_data(), (Dtype)., xw_norm_product_.mutable_cpu_data());//norm{wi}乘以norm{xj},输出维度为(M_,N_)
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasTrans, M_, N_, K_, (Dtype).,
bottom_data, weight, (Dtype)., cos_theta_.mutable_cpu_data());
caffe_add_scalar(M_ * N_, (Dtype)0.000000001, xw_norm_product_.mutable_cpu_data());//防止分母为0
caffe_div(M_ * N_, cos_theta_.cpu_data(), xw_norm_product_.cpu_data(), cos_theta_.mutable_cpu_data());//cos(theta),输出维度为(M_,N_) caffe_cpu_sign(M_ * N_, cos_theta_.cpu_data(), sign_0_.mutable_cpu_data()); switch (type_) {
case LargeMarginInnerProductParameter_LargeMarginType_SINGLE:
break;
case LargeMarginInnerProductParameter_LargeMarginType_DOUBLE:
caffe_powx(M_ * N_, cos_theta_.cpu_data(), (Dtype)., cos_theta_quadratic_.mutable_cpu_data());//cos(theta)^2,输出维度为(M_,N_)
break;
case LargeMarginInnerProductParameter_LargeMarginType_TRIPLE:
caffe_powx(M_ * N_, cos_theta_.cpu_data(), (Dtype)., cos_theta_quadratic_.mutable_cpu_data());
caffe_powx(M_ * N_, cos_theta_.cpu_data(), (Dtype)., cos_theta_cubic_.mutable_cpu_data());
caffe_abs(M_ * N_, cos_theta_.cpu_data(), sign_1_.mutable_cpu_data());
caffe_add_scalar(M_ * N_, -(Dtype)0.5, sign_1_.mutable_cpu_data());
caffe_cpu_sign(M_ * N_, sign_1_.cpu_data(), sign_1_.mutable_cpu_data());
caffe_copy(M_ * N_, sign_1_.cpu_data(), sign_2_.mutable_cpu_data());
caffe_add_scalar(M_ * N_, (Dtype)., sign_2_.mutable_cpu_data());
caffe_mul(M_ * N_, sign_0_.cpu_data(), sign_2_.cpu_data(), sign_2_.mutable_cpu_data());
caffe_add_scalar(M_ * N_, - (Dtype)., sign_2_.mutable_cpu_data());
break;
case LargeMarginInnerProductParameter_LargeMarginType_QUADRUPLE:
caffe_powx(M_ * N_, cos_theta_.cpu_data(), (Dtype)., cos_theta_quadratic_.mutable_cpu_data());
caffe_powx(M_ * N_, cos_theta_.cpu_data(), (Dtype)., cos_theta_cubic_.mutable_cpu_data());
caffe_powx(M_ * N_, cos_theta_.cpu_data(), (Dtype)., cos_theta_quartic_.mutable_cpu_data());
caffe_copy(M_ * N_, cos_theta_quadratic_.cpu_data(), sign_3_.mutable_cpu_data());
caffe_scal(M_ * N_, (Dtype)., sign_3_.mutable_cpu_data());
caffe_add_scalar(M_ * N_, (Dtype)-., sign_3_.mutable_cpu_data());
caffe_cpu_sign(M_ * N_, sign_3_.cpu_data(), sign_3_.mutable_cpu_data());
caffe_mul(M_ * N_, sign_0_.cpu_data(), sign_3_.cpu_data(), sign_3_.mutable_cpu_data());
caffe_copy(M_ * N_, sign_0_.cpu_data(), sign_4_.mutable_cpu_data());
caffe_scal(M_ * N_, (Dtype)., sign_4_.mutable_cpu_data());
caffe_add(M_ * N_, sign_4_.cpu_data(), sign_3_.cpu_data(), sign_4_.mutable_cpu_data());
caffe_add_scalar(M_ * N_, - (Dtype)., sign_4_.mutable_cpu_data());
break;
default:
LOG(FATAL) << "Unknown L-Softmax type.";
} /************************* Forward *************************/
Dtype* top_data = top[]->mutable_cpu_data();
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasTrans, M_, N_, K_, (Dtype).,
bottom_data, weight, (Dtype)., top_data);//top = XW’,X为bottom data维度为(M_,K_),W'为权重矩阵、维度为(K_,N_)
const Dtype* label = bottom[]->cpu_data();
const Dtype* xw_norm_product_data = xw_norm_product_.cpu_data();
switch (type_) {
case LargeMarginInnerProductParameter_LargeMarginType_SINGLE: {
break;
}
case LargeMarginInnerProductParameter_LargeMarginType_DOUBLE: {
const Dtype* sign_0_data = sign_0_.cpu_data();
const Dtype* cos_theta_quadratic_data = cos_theta_quadratic_.cpu_data();
for (int i = ; i < M_; i++) {
const int label_value = static_cast<int>(label[i]);
top_data[i * N_ + label_value] = xw_norm_product_data[i * N_ + label_value] *
((Dtype). * sign_0_data[i * N_ + label_value] *
cos_theta_quadratic_data[i * N_ + label_value] - (Dtype).);
}//修改样本i对应label的输出(请参考论文)
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasTrans, M_, N_, K_, lambda_,
bottom_data, weight, (Dtype)., top_data);//引入lambda_,加速收敛
caffe_scal(M_ * N_, (Dtype)./((Dtype). + lambda_), top_data);
break;//上述两个操作参考原始论文很好理解
}
case LargeMarginInnerProductParameter_LargeMarginType_TRIPLE: {
const Dtype* sign_1_data = sign_1_.cpu_data();
const Dtype* sign_2_data = sign_2_.cpu_data();
const Dtype* cos_theta_data = cos_theta_.cpu_data();
const Dtype* cos_theta_cubic_data = cos_theta_cubic_.cpu_data();
for (int i = ; i < M_; i++) {
const int label_value = static_cast<int>(label[i]);
top_data[i * N_ + label_value] = xw_norm_product_data[i * N_ + label_value] *
(sign_1_data[i * N_ + label_value] * ((Dtype). *
cos_theta_cubic_data[i * N_ + label_value] -
(Dtype). * cos_theta_data[i * N_ + label_value]) +
sign_2_data[i * N_ + label_value]);
}
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasTrans, M_, N_, K_, lambda_,
bottom_data, weight, (Dtype)., top_data);
caffe_scal(M_ * N_, (Dtype)./((Dtype). + lambda_), top_data);
break;
}
case LargeMarginInnerProductParameter_LargeMarginType_QUADRUPLE: {
const Dtype* sign_3_data = sign_3_.cpu_data();
const Dtype* sign_4_data = sign_4_.cpu_data();
const Dtype* cos_theta_quadratic_data = cos_theta_quadratic_.cpu_data();
const Dtype* cos_theta_quartic_data = cos_theta_quartic_.cpu_data();
for (int i = ; i < M_; i++) {
const int label_value = static_cast<int>(label[i]);
top_data[i * N_ + label_value] = xw_norm_product_data[i * N_ + label_value] *
(sign_3_data[i * N_ + label_value] * ((Dtype). *
cos_theta_quartic_data[i * N_ + label_value] -
(Dtype). * cos_theta_quadratic_data[i * N_ + label_value] +
(Dtype).) + sign_4_data[i * N_ + label_value]);
}
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasTrans, M_, N_, K_, lambda_,
bottom_data, weight, (Dtype)., top_data);
caffe_scal(M_ * N_, (Dtype)./((Dtype). + lambda_), top_data);
break;
}
default: {
LOG(FATAL) << "Unknown L-Softmax type.";
}
}
} //在反向传播中,我只简单介绍一下核心的误差传递,忽略导数的计算公式分析。计算公式参考论文是很好理解的
template <typename Dtype>
void LargeMarginInnerProductLayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top,
const vector<bool>& propagate_down,
const vector<Blob<Dtype>*>& bottom) {
Blob<Dtype> inv_w_norm_;
inv_w_norm_.Reshape(w_norm_.shape());
Blob<Dtype> xw_norm_ratio_;
xw_norm_ratio_.Reshape(cos_theta_.shape());
caffe_add_scalar(N_, (Dtype)0.000000001, w_norm_.mutable_cpu_data());
caffe_set(N_, (Dtype)., inv_w_norm_.mutable_cpu_data());
caffe_div(N_, inv_w_norm_.cpu_data(), w_norm_.cpu_data(), inv_w_norm_.mutable_cpu_data());
caffe_cpu_gemm<Dtype>(CblasTrans, CblasNoTrans, M_, N_, , (Dtype).,
x_norm_.cpu_data(), inv_w_norm_.cpu_data(), (Dtype)., xw_norm_ratio_.mutable_cpu_data()); const Dtype* top_diff = top[]->cpu_diff();
const Dtype* bottom_data = bottom[]->cpu_data();
const Dtype* label = bottom[]->cpu_data();
const Dtype* weight = this->blobs_[]->cpu_data(); if (this->param_propagate_down_[]) {
Dtype* weight_diff = this->blobs_[]->mutable_cpu_diff();//请注意:weight和weight_diff含义不同
const Dtype* xw_norm_ratio_data = xw_norm_ratio_.cpu_data();
switch (type_) {
case LargeMarginInnerProductParameter_LargeMarginType_SINGLE: {
caffe_cpu_gemm<Dtype>(CblasTrans, CblasNoTrans, N_, K_, M_, (Dtype).,
top_diff, bottom_data, (Dtype)., this->blobs_[]->mutable_cpu_diff());
break;
}
case LargeMarginInnerProductParameter_LargeMarginType_DOUBLE: {
const Dtype* sign_0_data = sign_0_.cpu_data();
const Dtype* cos_theta_data = cos_theta_.cpu_data();
const Dtype* cos_theta_quadratic_data = cos_theta_quadratic_.cpu_data();
for (int i = ; i < N_; i++) {
for (int j = ; j < M_; j++) {// dL/dwij = sum{dL/dfni*dfni/dwij},求和范围n属于[0,M_)
const int label_value = static_cast<int>(label[j]);
if (label_value != i) {
caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[j * N_ + i],
bottom_data + j * K_, (Dtype)., weight_diff + i * K_);
} else {
caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[j * N_ + i] *
(Dtype). * sign_0_data[j * N_ + i] * cos_theta_data[j * N_ + i],
bottom_data + j * K_, (Dtype)., weight_diff + i * K_);
caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[j * N_ + i] *
(-xw_norm_ratio_data[j * N_ + i]) * ((Dtype). * sign_0_data[j * N_ + i] *
cos_theta_quadratic_data[j * N_ + i] + (Dtype).),
weight + i * K_, (Dtype)., weight_diff + i * K_);
}
}
}
caffe_cpu_gemm<Dtype>(CblasTrans, CblasNoTrans, N_, K_, M_, lambda_/((Dtype). + lambda_),
top_diff, bottom_data, (Dtype)., this->blobs_[]->mutable_cpu_diff());
break;
}
case LargeMarginInnerProductParameter_LargeMarginType_TRIPLE: {
const Dtype* sign_1_data = sign_1_.cpu_data();
const Dtype* sign_2_data = sign_2_.cpu_data();
const Dtype* cos_theta_quadratic_data = cos_theta_quadratic_.cpu_data();
const Dtype* cos_theta_cubic_data = cos_theta_cubic_.cpu_data();
for (int i = ; i < N_; i++) {
for (int j = ; j < M_; j++) {
const int label_value = static_cast<int>(label[j]);
if (label_value != i) {
caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[j * N_ + i],
bottom_data + j * K_, (Dtype)., weight_diff + i * K_);
} else {
caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[j * N_ + i] *
sign_1_data[j * N_ + i] * ((Dtype). * cos_theta_quadratic_data[j * N_ + i] -
(Dtype).),
bottom_data + j * K_, (Dtype)., weight_diff + i * K_);
caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[j * N_ + i] *
(-xw_norm_ratio_data[j * N_ + i]) * ((Dtype). * sign_1_data[j * N_ + i] *
cos_theta_cubic_data[j * N_ + i] - sign_2_data[j * N_ + i]),
weight + i * K_, (Dtype)., weight_diff + i * K_);
}
}
}
caffe_cpu_gemm<Dtype>(CblasTrans, CblasNoTrans, N_, K_, M_, lambda_/((Dtype). + lambda_),
top_diff, bottom_data, (Dtype)., this->blobs_[]->mutable_cpu_diff());
break;
}
case LargeMarginInnerProductParameter_LargeMarginType_QUADRUPLE: {
const Dtype* sign_3_data = sign_3_.cpu_data();
const Dtype* sign_4_data = sign_4_.cpu_data();
const Dtype* cos_theta_data = cos_theta_.cpu_data();
const Dtype* cos_theta_quadratic_data = cos_theta_quadratic_.cpu_data();
const Dtype* cos_theta_cubic_data = cos_theta_cubic_.cpu_data();
const Dtype* cos_theta_quartic_data = cos_theta_quartic_.cpu_data();
for (int i = ; i < N_; i++) {
for (int j = ; j < M_; j++) {
const int label_value = static_cast<int>(label[j]);
if (label_value != i) { caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[j * N_ + i],
bottom_data + j * K_, (Dtype)., weight_diff + i * K_);
} else { caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[j * N_ + i] *
sign_3_data[j * N_ + i] * ((Dtype). * cos_theta_cubic_data[j * N_ + i] -
(Dtype). * cos_theta_data[j * N_ + i]),
bottom_data + j * K_, (Dtype)., weight_diff + i * K_); caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[j * N_ + i] *
(-xw_norm_ratio_data[j * N_ + i]) * (sign_3_data[j * N_ + i] *
((Dtype). * cos_theta_quartic_data[j * N_ + i] -
(Dtype). * cos_theta_quadratic_data[j * N_ + i] - (Dtype).) -
sign_4_data[j * N_ + i]),
weight + i * K_, (Dtype)., weight_diff + i * K_);
}
}
} caffe_cpu_gemm<Dtype>(CblasTrans, CblasNoTrans, N_, K_, M_, lambda_/((Dtype). + lambda_),
top_diff, bottom_data, (Dtype)., this->blobs_[]->mutable_cpu_diff());
break;
}
default: {
LOG(FATAL) << "Unknown L-Softmax type.";
}
}
} // Gradient with respect to bottom data
if (propagate_down[]) {
Dtype* bottom_diff = bottom[]->mutable_cpu_diff();
const Dtype* xw_norm_ratio_data = xw_norm_ratio_.cpu_data();
caffe_set(M_ * K_, (Dtype)., bottom_diff);
switch (type_) {
case LargeMarginInnerProductParameter_LargeMarginType_SINGLE: {
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, M_, K_, N_, (Dtype).,
top_diff, this->blobs_[]->cpu_data(), (Dtype).,
bottom[]->mutable_cpu_diff());
break;
}
case LargeMarginInnerProductParameter_LargeMarginType_DOUBLE: {
const Dtype* sign_0_data = sign_0_.cpu_data();
const Dtype* cos_theta_data = cos_theta_.cpu_data();
const Dtype* cos_theta_quadratic_data = cos_theta_quadratic_.cpu_data();
for (int i = ; i < M_; i++) {
const int label_value = static_cast<int>(label[i]);
for (int j = ; j < N_; j++) {// dL/dxij = sum{dL/dfin*dfin/dxij},求和范围n属于[0,N_)
if (label_value != j) { caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[i * N_ + j],
weight + j * K_, (Dtype)., bottom_diff + i * K_);
} else { caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[i * N_ + j] *
(Dtype). * sign_0_data[i * N_ + j] * cos_theta_data[i * N_ + j],
weight + j * K_, (Dtype)., bottom_diff + i * K_); caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[i * N_ + j] /
(-xw_norm_ratio_data[i * N_ + j]) * ((Dtype). * sign_0_data[i * N_ + j] *
cos_theta_quadratic_data[i * N_ + j] + (Dtype).),
bottom_data + i * K_, (Dtype)., bottom_diff + i * K_);
}
}
} caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, M_, K_, N_, lambda_/((Dtype). + lambda_),
top_diff, this->blobs_[]->cpu_data(), (Dtype).,
bottom[]->mutable_cpu_diff());
break;
}
case LargeMarginInnerProductParameter_LargeMarginType_TRIPLE: {
const Dtype* sign_1_data = sign_1_.cpu_data();
const Dtype* sign_2_data = sign_2_.cpu_data();
const Dtype* cos_theta_quadratic_data = cos_theta_quadratic_.cpu_data();
const Dtype* cos_theta_cubic_data = cos_theta_cubic_.cpu_data();
for (int i = ; i < M_; i++) {
const int label_value = static_cast<int>(label[i]);
for (int j = ; j < N_; j++) {
if (label_value != j) {
caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[i * N_ + j],
weight + j * K_, (Dtype)., bottom_diff + i * K_);
} else { caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[i * N_ + j] *
sign_1_data[i * N_ + j] * ((Dtype). * cos_theta_quadratic_data[i * N_ + j] -
(Dtype).),
weight + j * K_, (Dtype)., bottom_diff + i * K_); caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[i * N_ + j] /
(-xw_norm_ratio_data[i * N_ + j]) * ((Dtype). * sign_1_data[i * N_ + j] *
cos_theta_cubic_data[i * N_ + j] - sign_2_data[i * N_ +j]),
bottom_data + i * K_, (Dtype)., bottom_diff + i * K_);
}
}
} caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, M_, K_, N_, lambda_/((Dtype). + lambda_),
top_diff, this->blobs_[]->cpu_data(), (Dtype).,
bottom[]->mutable_cpu_diff());
break;
}
case LargeMarginInnerProductParameter_LargeMarginType_QUADRUPLE: {
const Dtype* sign_3_data = sign_3_.cpu_data();
const Dtype* sign_4_data = sign_4_.cpu_data();
const Dtype* cos_theta_data = cos_theta_.cpu_data();
const Dtype* cos_theta_quadratic_data = cos_theta_quadratic_.cpu_data();
const Dtype* cos_theta_cubic_data = cos_theta_cubic_.cpu_data();
const Dtype* cos_theta_quartic_data = cos_theta_quartic_.cpu_data();
for (int i = ; i < M_; i++) {
const int label_value = static_cast<int>(label[i]);
for (int j = ; j < N_; j++) {
if (label_value != j) {
caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[i * N_ + j],
weight + j * K_, (Dtype)., bottom_diff + i * K_);
} else { caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[i * N_ + j] *
sign_3_data[i * N_ + j] * ((Dtype). * cos_theta_cubic_data[i * N_ + j] -
(Dtype). * cos_theta_data[i * N_ + j]),
weight + j * K_, (Dtype)., bottom_diff + i * K_); caffe_cpu_axpby(K_, (Dtype). / ((Dtype). + lambda_) * top_diff[i * N_ + j] /
(-xw_norm_ratio_data[i * N_ + j]) * (sign_3_data[i * N_ + j] *
((Dtype). * cos_theta_quartic_data[i * N_ + j] -
(Dtype). * cos_theta_quadratic_data[i * N_ + j] - (Dtype).) -
sign_4_data[i * N_ + j]),
bottom_data + i * K_, (Dtype)., bottom_diff + i * K_);
}
}
}
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, M_, K_, N_, lambda_/((Dtype). + lambda_),
top_diff, this->blobs_[]->cpu_data(), (Dtype).,
bottom[]->mutable_cpu_diff());
break;
}
default: {
LOG(FATAL) << "Unknown L-Softmax type.";
}
}
}
} #ifdef CPU_ONLY
STUB_GPU(LargeMarginInnerProductLayer);
#endif INSTANTIATE_CLASS(LargeMarginInnerProductLayer);
REGISTER_LAYER_CLASS(LargeMarginInnerProduct); } // namespace caffe
反向传播时我只示例性的展示了链式法则(有d代表偏导符号∂了)。如果大家觉得lambda碍事,可以直接认为其值为0,这样能够简化我们的理解。
GPU实现部分原理应该差不多,只是实现方式有所差异,这里我就不进行分析了。大家可以参考这篇说明理解这篇论文的基本原理https://mp.weixin.qq.com/s?__biz=MzA3Mjk0OTgyMg==&mid=2651123524&idx=1&sn=0546ceca3d88e2ff1e66fbecc99bd6a7&chksm=84e6c615b3914f03bec98f22eefb00da5b30a82866c068cc4045e3ee9d0a31366f2f8bb5fec1&scene=0&ptlang=2052&source&ADUIN=1184611233&ADSESSION=1496371074&ADTAG=CLIENT.QQ.5527_.0&ADPUBNO=26632#rd
总结:通过阅读源码,我明白了链式法则在程序中是如何运用的,也学到了一个加速网络收敛的技巧(即引入指数退化项)。
源码分析 Large-Margin Softmax Loss for Convolutional Neural Networks的更多相关文章
- Large-Margin Softmax Loss for Convolutional Neural Networks
paper url: https://arxiv.org/pdf/1612.02295 year:2017 Introduction 交叉熵损失与softmax一起使用可以说是CNN中最常用的监督组件 ...
- 基于Caffe的Large Margin Softmax Loss的实现(中)
小喵的唠叨话:前一篇博客,我们做完了L-Softmax的准备工作.而这一章,我们开始进行前馈的研究. 小喵博客: http://miaoerduo.com 博客原文: http://www.miao ...
- 基于Caffe的Large Margin Softmax Loss的实现(上)
小喵的唠叨话:在写完上一次的博客之后,已经过去了2个月的时间,小喵在此期间,做了大量的实验工作,最终在使用的DeepID2的方法之后,取得了很不错的结果.这次呢,主要讲述一个比较新的论文中的方法,L- ...
- Large Margin Softmax Loss for Speaker Verification
[INTERSPEECH 2019接收] 链接:https://arxiv.org/pdf/1904.03479.pdf 这篇文章在会议的speaker session中.本文主要讨论了说话人验证中的 ...
- 源码分析——迁移学习Inception V3网络重训练实现图片分类
1. 前言 近些年来,随着以卷积神经网络(CNN)为代表的深度学习在图像识别领域的突破,越来越多的图像识别算法不断涌现.在去年,我们初步成功尝试了图像识别在测试领域的应用:将网站样式错乱问题.无线领域 ...
- BERT源码分析
一.整体 整个代码文件如下: 二.tensorflow基础 1.tf.expand_dims 作用:给定张量“ input”,此操作将在“ input”形状的尺寸索引“ axis”处插入尺寸为1的尺寸 ...
- FastText总结,fastText 源码分析
文本分类单层网络就够了.非线性的问题用多层的. fasttext有一个有监督的模式,但是模型等同于cbow,只是target变成了label而不是word. fastText有两个可说的地方:1 在w ...
- spark源码分析以及优化
第一章.spark源码分析之RDD四种依赖关系 一.RDD四种依赖关系 RDD四种依赖关系,分别是 ShuffleDependency.PrunDependency.RangeDependency和O ...
- Alink漫谈(十六) :Word2Vec源码分析 之 建立霍夫曼树
Alink漫谈(十六) :Word2Vec源码分析 之 建立霍夫曼树 目录 Alink漫谈(十六) :Word2Vec源码分析 之 建立霍夫曼树 0x00 摘要 0x01 背景概念 1.1 词向量基础 ...
随机推荐
- java复习(5)---接口、继承、多态
Java作为完全面向对象语言,接口.继承和多态是三个非常重要的概念. 1.继承. (1)关键字: extends (2)子类用super()调用父类构造函数,用super().方法 调用父类的成员方法 ...
- js 解析本地Excel文件!
通常,一般读取Excel都是由后台来处理,不过如果需求要前台来处理,也是可以的.. 1.需要用到js-xlsx,下载地址:js-xlsx 2.demo: <!DOCTYPE html>&l ...
- CF #356 div1 A. Bear and Prime 100
题目链接:http://codeforces.com/contest/679/problem/A CF有史以来第一次出现交互式的题目,大致意思为选择2到100中某一个数字作为隐藏数,你可以询问最多20 ...
- Amazon Alexa登录授权(Android)
访问Alexa的API,必须要携带AccessToken,也就是必须要登录授权,本文主要记录Amazon Alexa在Android平台上的登录授权过程. 一.在亚马逊开发者平台注册应用 进入亚马逊开 ...
- python基本数据类型——int
一.int的范围 python2: 在32位机器上,整数的位数为32位,取值范围为-2**31-2**31-1: 在64位系统上,整数的位数为64位,取值范围为-2**63-2**63-1: pyth ...
- 0基础搭建Hadoop大数据处理-初识
在互联网的世界中数据都是以TB.PB的数量级来增加的,特别是像BAT光每天的日志文件一个盘都不够,更何况是还要基于这些数据进行分析挖掘,更甚者还要实时进行数据分析,学习,如双十一淘宝的交易量的实时展示 ...
- Maven的pom.xml配置文件详解
Maven简述 Maven项目对象模型(POM),可以通过一小段描述信息来管理项目的构建,报告和文档的软件项目管理工具. Maven 除了以程序构建能力为特色之外,还提供高级项目管理工具.由于 Mav ...
- Pangolin学习
0.1. 资料 0.2. 使用说明 0.3. HelloPangolin 0.4. Plot data with ros 0.1. 资料 泡泡机器人 github example opengl中摄像机 ...
- POJ3252-Round Numbers 数学
题目链接:http://poj.org/problem?id=3252 题目大意: 输入两个十进制正整数a和b,求闭区间 [a ,b] 内有多少个Round number 所谓的Round Numbe ...
- mysql语句优化总结(一)
Sql语句优化和索引 1.Innerjoin和左连接,右连接,子查询 A. inner join内连接也叫等值连接是,left/rightjoin是外连接. SELECT A.id,A.nam ...
