HDU 6097---Mindis(二分)

题目链接

Problem Description

The center coordinate of the circle C is O, the coordinate of O is (0,0) , and the radius is r.
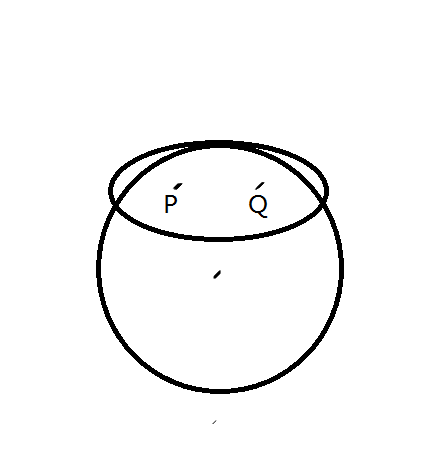
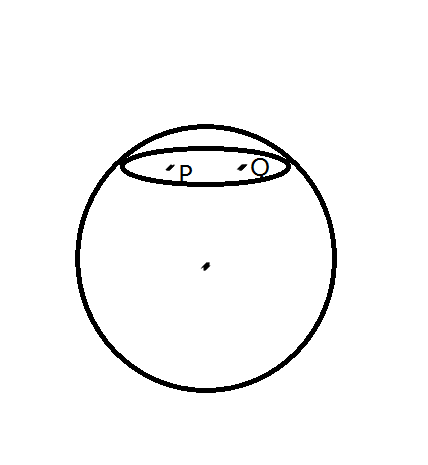
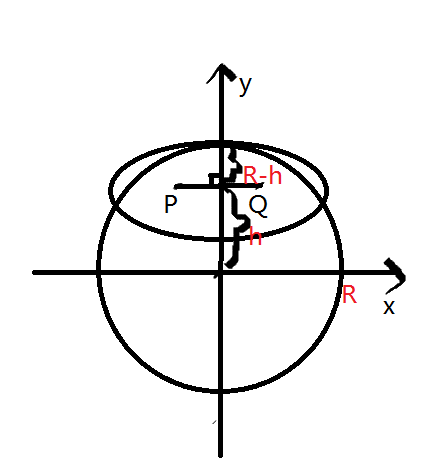
P and Q are two points not outside the circle, and PO = QO.
You need to find a point D on the circle, which makes PD+QD minimum.
Output minimum distance sum.

 

Input

The first line of the input gives the number of test cases T; T test cases follow.
Each case begins with one line with r : the radius of the circle C.
Next two line each line contains two integers x , y denotes the coordinate of P and Q.

Limits
T≤500000
−100≤x,y≤100
1≤r≤100

 

Output

For each case output one line denotes the answer.
The answer will be checked correct if its absolute or relative error doesn't exceed 10−6.
Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if |a−b|max(1,b)≤10−6.

 

Sample Input

4

4

4 0

0 4 

4

0 3

3 0

4

0 2

2 0

4

0 1

1 0

 

Sample Output

5.6568543

5.6568543

5.8945030

6.7359174

 

题意：有一个圆，圆心在原点，输入半径 r ，圆内有两个点P ， Q 到圆心距离相同，现在求在圆上找一点M，使得PM+QM最小？

 

思路：

            

      对于圆内的两个点 P 和 Q ，如果以其作为椭圆两个焦点，由图一可以看到：当椭圆顶点与圆相切时 ， 圆与椭圆会有三个焦点，而椭圆上的点到P、Q的距离和是定值。那么可以缩小椭圆，接下来会有四个交点，继续缩小椭圆，得到图二，椭圆与圆只有两个交点，因为椭圆外的点到两个焦点的距离和大于2a，而椭圆上的点到两个焦点的距离和为2a,。在图2中，除了两个交点外，其余圆上点均在椭圆外，所以这时的交点到P、Q两点的距离和最小，等于2a。

      如何找到这个相切的椭圆呢？二分解决。

      具体：由P、Q两个焦点，我们可以确定c=PQ/2 ,  现在如果再给出一个b值那么就能确定这个椭圆了，而b值越大椭圆越大，b值越小椭圆越小，所以我们要找到如图2所示，相切只有两个焦点时的b值，那么我们需要找的就是圆和椭圆相交时最小的b。我们可以求出图3中所示的 h 和 R -h ，那么椭圆的方程为：x^2/a^2 + (y-h)^2/b^2 = 1 ( 这个方程是PQ平行于X轴时的，但PQ不平行于X时也不影响，我们只是用它判断是否与圆相交 ) 圆：x^2 + y^2 =R^R ,    并且b>0（显然），b<R-h ，所以在（0，R-h） 二分查找b。

 

代码如下：

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <algorithm>
using namespace std;
const double eps = 1e-;
double dis(double x1,double y1,double x2,double y2 )
{
    return sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
}
namespace IO {
    const int MX = 4e7; //1e7占用内存11000kb
    char buf[MX]; int c, sz;
    void begin() {
        c = ;
        sz = fread(buf, , MX, stdin);
    }
    inline bool read(int &t) {
        while(c < sz && buf[c] != '-' && (buf[c] < '' || buf[c] > '')) c++;
        if(c >= sz) return false;
        bool flag = ; if(buf[c] == '-') flag = , c++;
        for(t = ; c < sz && '' <= buf[c] && buf[c] <= ''; c++) t = t *  + buf[c] - '';
        if(flag) t = -t;
        return true;
    }
}

int main()
{
    IO::begin();
    int T;
    double R,x1,x2,y1,y2;
    double x3,y3;
    double A,B,C,dt,ans1,ans2;
    //cin>>T;
    IO::read(T);
    while(T--)
    {
        //scanf("%lf%lf%lf%lf%lf",&R,&x1,&y1,&x2,&y2);
        int xr, xx1, xx2, yy1, yy2;
        IO::read(xr);
        IO::read(xx1);
        IO::read(yy1);
        IO::read(xx2);
        IO::read(yy2);
        R = xr;
        x1 = xx1;y1 = yy1;x2 = xx2;y2 = yy2;
        double c=dis(x1,y1,x2,y2)*0.5;
        c=c*c;
        x3=(x1+x2)*0.5;
        y3=(y1+y2)*0.5;
        double h=dis(x3,y3,0.0,0.0);
        //cout<<h<<endl;
        double Rb=R-h;
        double Lb=0.0,b,a,mid;

        for(int i=; i<; i++)
        {
            mid=(Lb+Rb)*0.5;
            b = mid;
            b=b*b;
            a=c+b;
            A=a-b;
            B=2.0*a*h;
            C=b*R*R+a*h*h-a*b;
            dt=B*B-4.0*A*C;
            int flag=;
            if(dt>=-eps)
            {
                ans1=(-B+sqrt(B*B-4.0*A*C))*0.5/A;
                ans2=(-B-sqrt(B*B-4.0*A*C))*0.5/A;
                ans1=ans1*ans1;
                ans2=ans2*ans2;
                if(R*R-ans1>=-eps||R*R-ans2>=-eps)
                    flag=;
            }
            if(flag==)
                Rb=mid;
            else
                Lb=mid;
        }
        printf("%.10f\n",sqrt(a)*2.0);

    }
    return ;
}