Ricequant-米筐金工-估值因子

Ricequant米筐金工——因子分析

作者：戴宇、小湖

上一篇介绍了单因子检验是因子分析前重要的一个步骤，是构建因子库、建立因子模型的基础，这篇报告首先对常见估值因子进行初步的检验。

第一篇．估值因子的分析

估值因子是一类具有特色的风格因子，本报告选取了PE，PB，PCF，PS，PEG五个常见的估值因子进行因子分析，测试区间是2014年1月1日~2017年8月1日，测试数据是全市场股票的月数据，主要从有效性和稳定性两个角度分析因子。

通过此次报告可以初步得出以下结论：

1、  此次选择的五个估值类因子的行业分布存在一定相似性，在银行、钢铁行业的暴露度普遍偏低，在通信行业、医药生物行业的估值因子的暴露度较高。

2、  通过观察因子暴露度在不同市值区间的分布差异，估值类因子与市值有轻微的递减关系，说明因子暴露度与市值存在一定关联。

3、  IC和RANK-IC两种计算因子暴露度与收益率相关系数的方式有差异，RANK-IC的显著性水平较低（p值较低），RANK-IC的绝对值较大，在时间序列上波动性较大。

4、  PE因子暴露度与收益率的负相关性的关系较明显，并且这种趋势持续时间较长，peg因子显著的状态切换比例和同向比例均较大，说明大部分情况下peg因子的相关系数较显著，但是难以判断peg因子与收益率关系的方向。

5、  所选估值因子中PE、PCF、PEG的同向显著比例普遍比状态切换显著比例大，说明在这三个因子最近一年存在趋势性。

6、  所选估值因子的负相关显著比例比正相关显著比例高，在最近一年的IC和RANK-IC的6月移动平均值都小于零，并且在负半轴上的绝对值有增大的趋势，说明在最近一年估值因子暴露度与因子收益率的大部分时间可能存在负相关关系。

7、  PB、PEG因子的IC分布直方图处于小于零的部分大于大于零的部分。

常见估值因子及其描述

表1

大类因子	具体因子	因子描述
估值因子	PB	市净率，每股股价与每股净资产的比率
	PE	市盈率，公司当时股价与每股盈利的比率，股价一般以最新收盘价
	PEG	市盈率相对盈利增长比率
	PS	市销率，指股票价格与每股销售收入之比
	PCF	市现率，股票价格与每股现金流量的比率

一、因子暴露度在不同行业的分布差异：

因子在行业之间的平均暴露度存在差距，以2017年8月1日为例。

图1到5展示了因子暴露度在不同行业的分布差异

通过对比各个因子暴露度的行业分布差异，银行行业平均暴露度最小的因子有PCF，PE，PB。各个因子在钢铁行业的平均暴露度均较小，在通信行业的平均暴露度都比较大。

图1展示了PB因子在食品饮料行业的平均暴露度最大，在钢铁、银行行业的平均暴露度最小。

图2展示了PE因子在通信行业的平均暴露度最大，在银行行业的平均暴露度最小

图3展示了PEG因子在一些综合性的股票中平均暴露度较大，在电气设备行业的平均暴露度最大，在钢铁行业的平均暴露度最小。

图4展示了PS因子在休闲服务行业的平均暴露度最大，在钢铁行业的平均暴露度最小。

图5展示了PCF因子在通信行业的平均暴露度最大，在银行行业的平均暴露度最小。

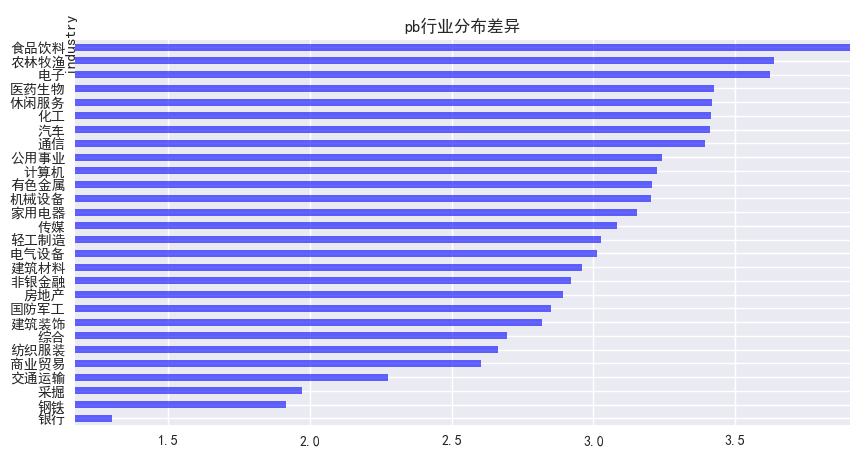
图1   PB行业分布差异

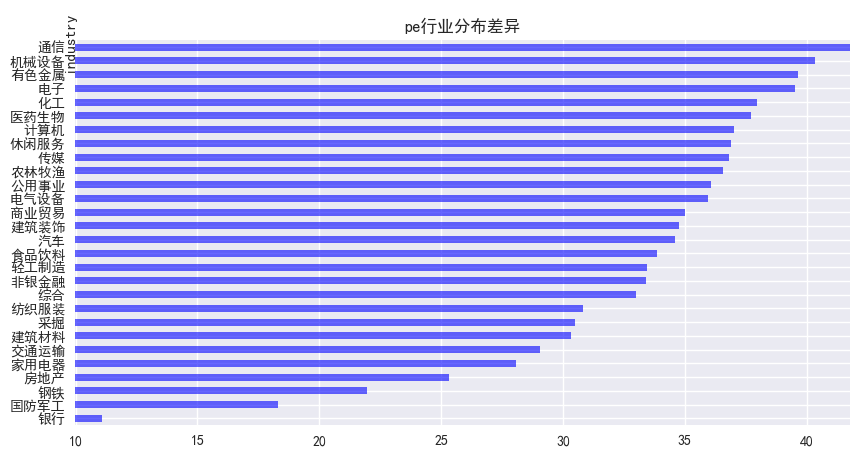
图2   PE行业分布差异

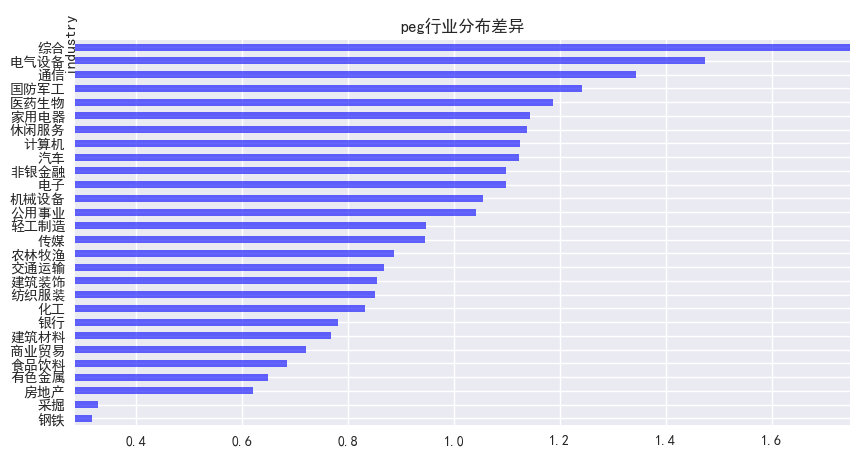
图3   PEG行业分布差异

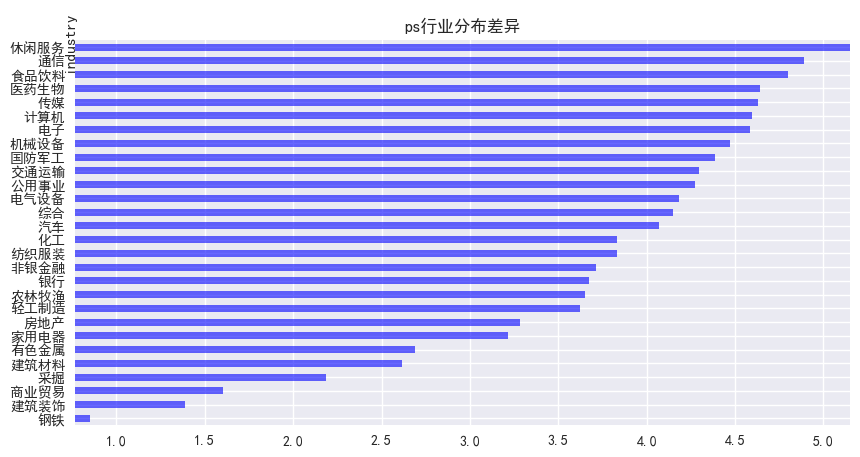
图4  PS行业分布差异

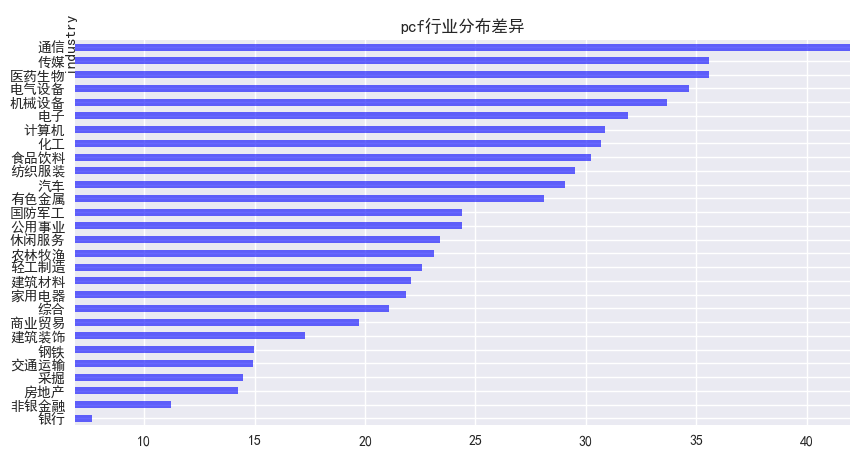
图5   PCF行业分布差异

二、因子暴露度在不同市值区间的分布差异

图6到图10展示了因子暴露度在不同市值区间的分布差异

因子暴露度在横截面和时间序列上均存在差异，即不同时间的同一个因子的暴露度存在差异，不同市值区间的因子暴露度也存在不同，此次报告中的5个因子都在某一时间段与市值有递减关系。

图6展示了PB因子在2015年的普遍暴露度较高，并且可以看出一般低市值股票具有较高的PB暴露度。

图7展示了PCF因子在2015年和2016年的暴露度较高，在2014年和2017年，一般低市值股票具有较高的PCF暴露度。

图8展示了PE因子在2015年和2016年的暴露度较高，在2014年和2017年的有明显的市值区分，与市值有递减的关系

图9展示了PEG因子在2015年和2016年的暴露度较高，在2017年与市值有递减的关系。

图10展示了PS因子在2014年暴露度较低，在2014年和2015年市值区间之间没有显著的差异，在2016年和2017年与市值有稍微的递减关系

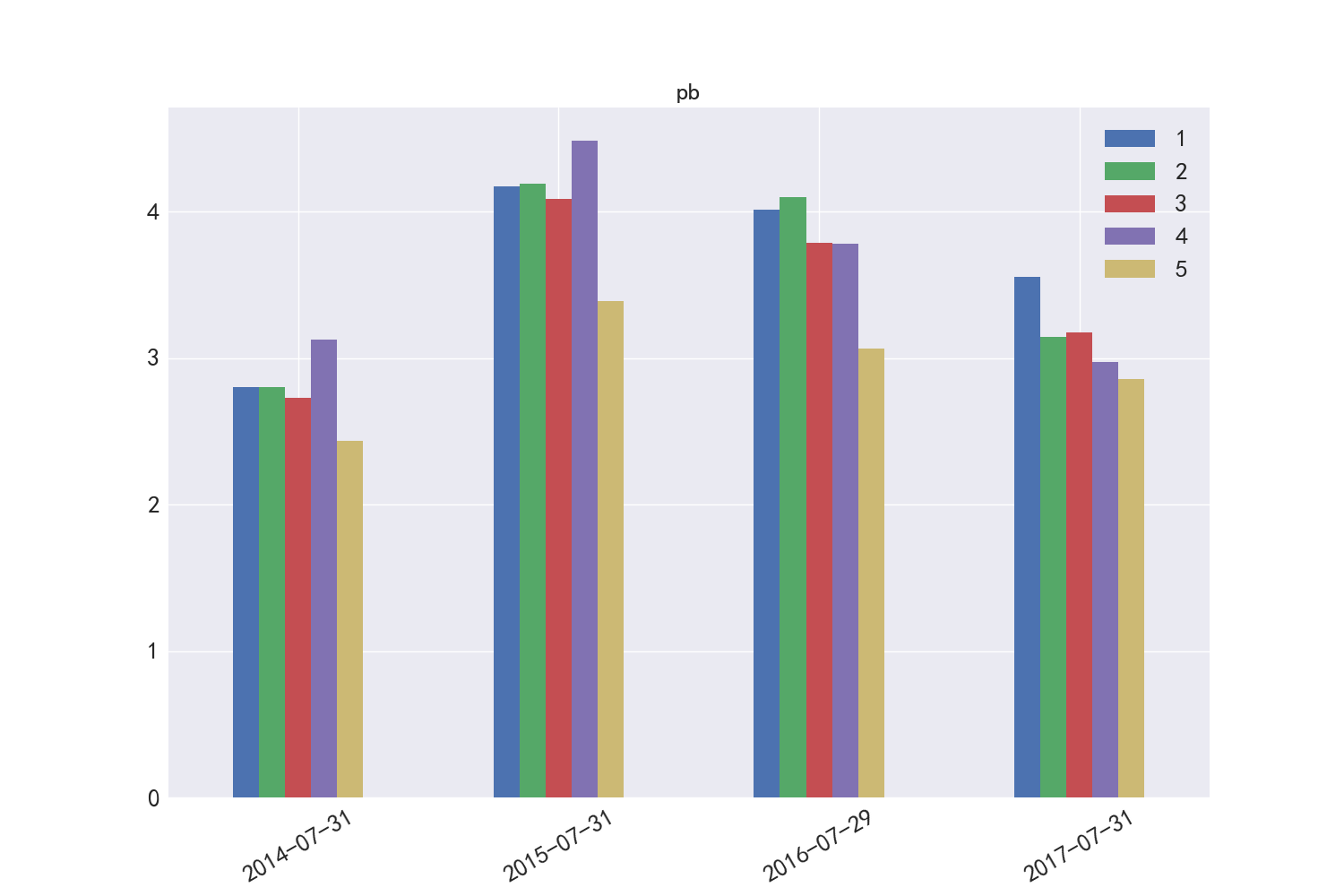
图6   PB市值分布差异

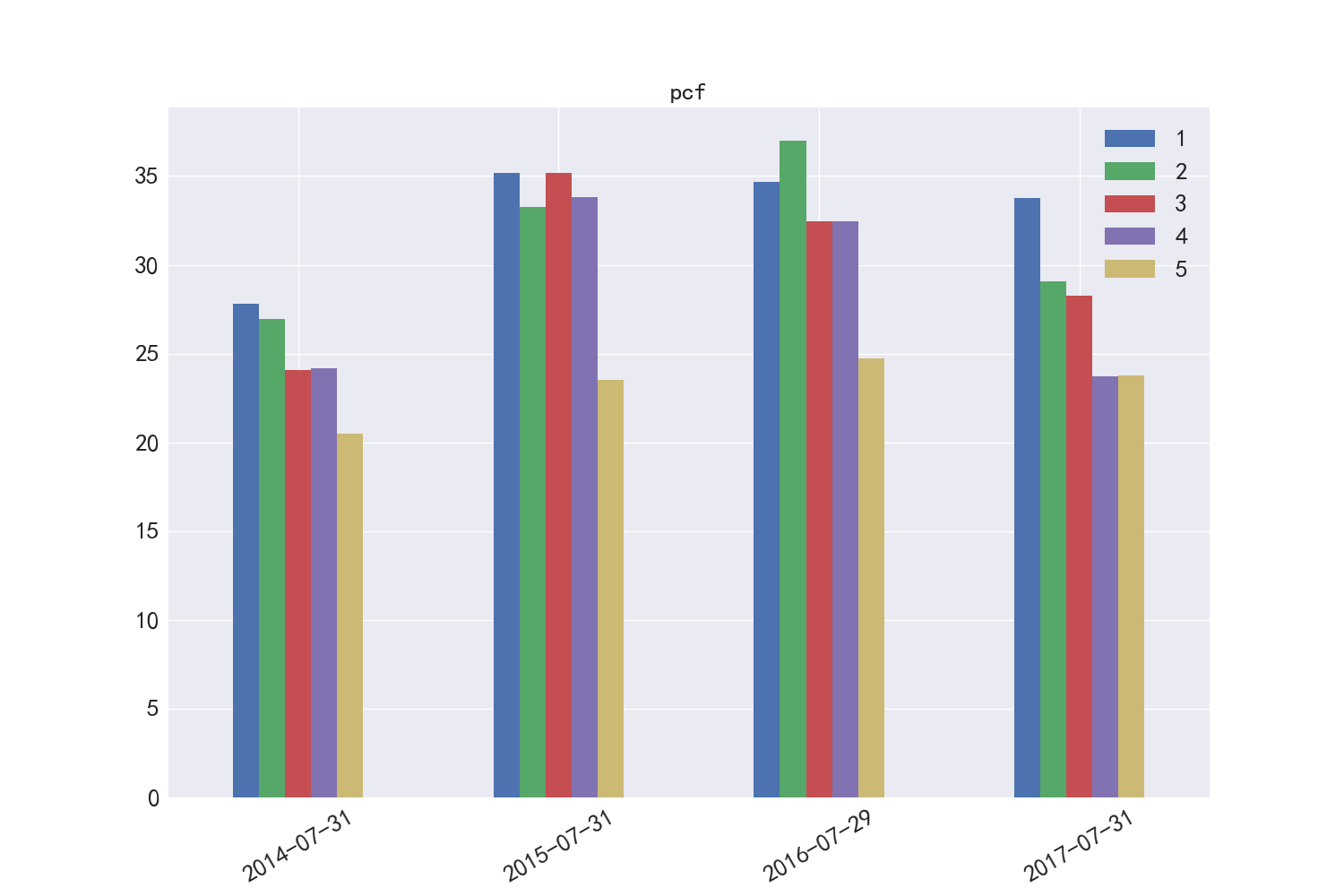
图7   PCF市值分布差异

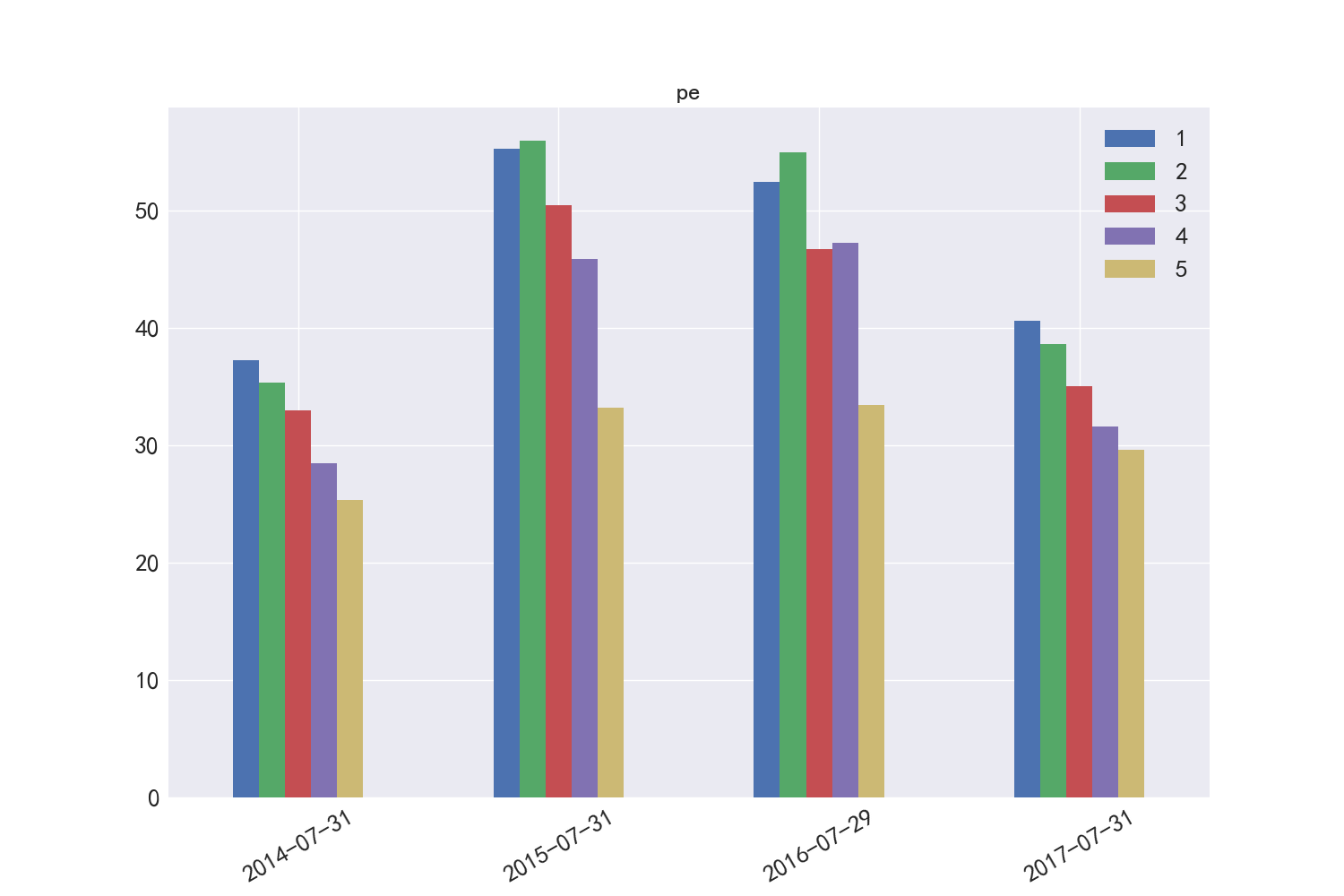
图8   PE市值分布差异

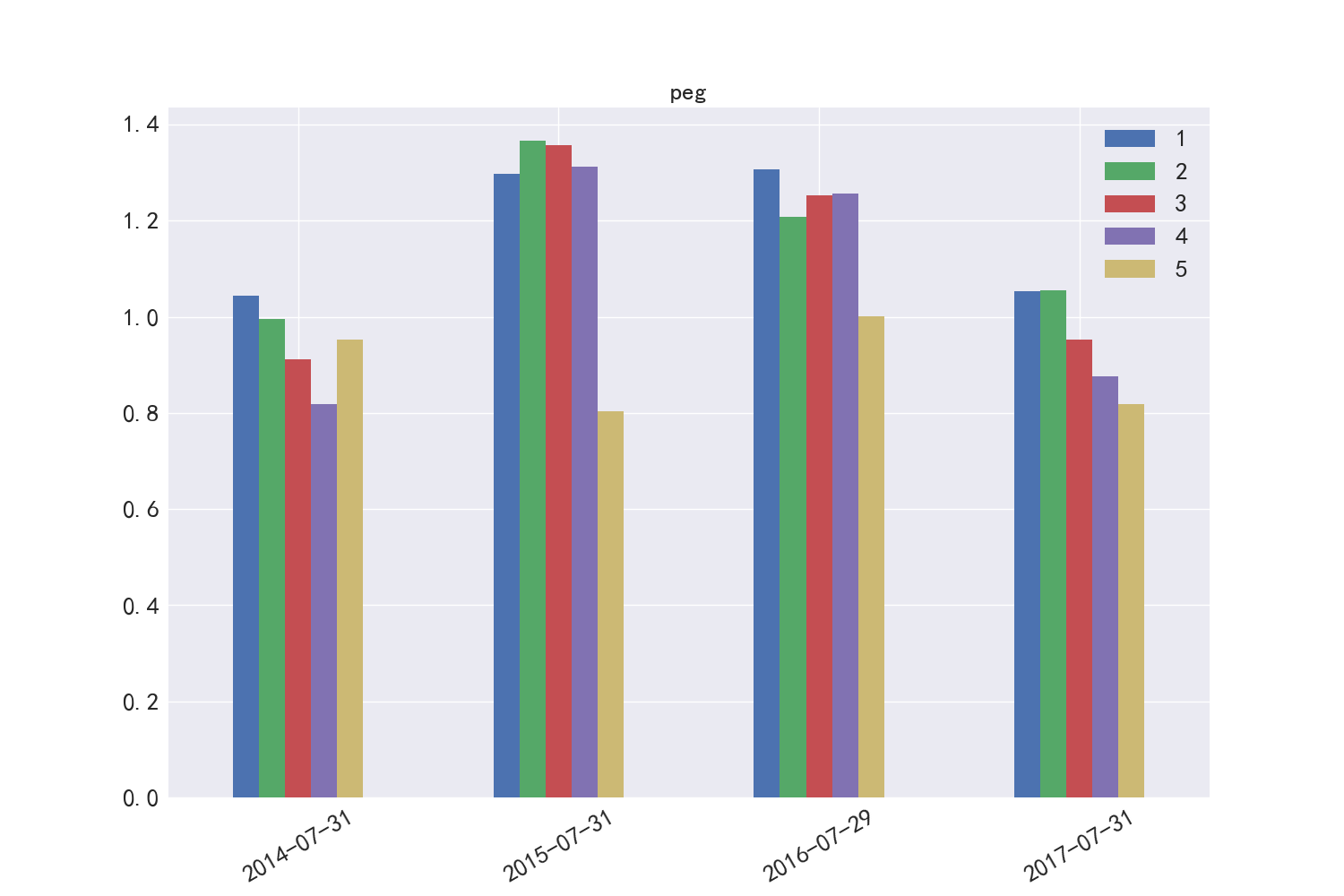
图9   PEG市值分布差异

图10   PS市值分布差异

三、因子暴露度的相关关系和自相关性

因子暴露度的相互关系

图11和图12展示了因子暴露度的平均相关性

基于2014年1月1日到2017年8月1日PB、PE、PCF、PS、PEG的暴露度数据，计算得到各因子之间的平均相关性如图11、图12所示。可以看出估值大类因子下的细分因子之间相关性都没有预期的高，其中相关性比较明显的是PCF和PE，PCF和PS，PCF和PB因子。

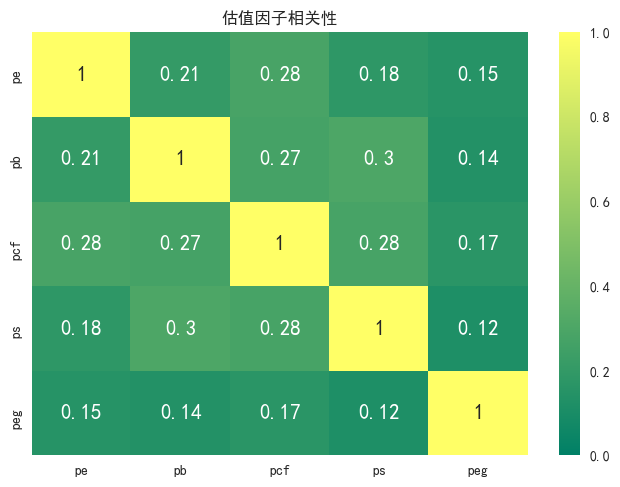
图11       估值因子暴露度的pearson相关性

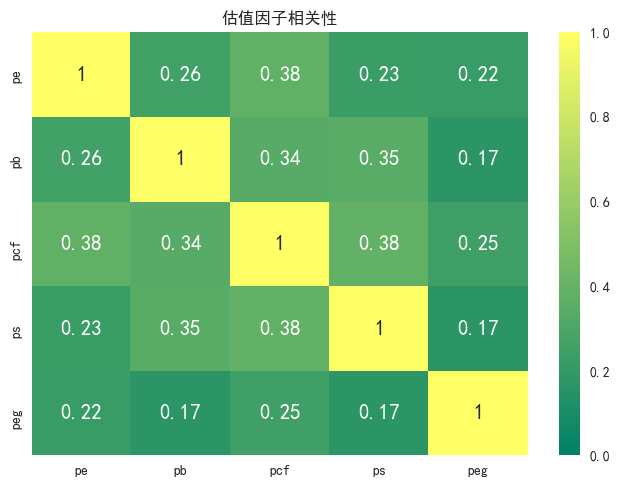
图12       估值因子暴露度的spearman相关性

因子暴露度的自相关关系

图13到图17展示了因子暴露度的自相关系数

同时，我们通过计算各子类因子的自相关性发现：各因子的自相关性绝大多数都是稳定衰减的；图15展示了PEG因子的自相关性的衰减速率较快，在第一期到第七期自相关性急速下降；图17展示了PS因子的自相关性下降最缓慢，而且通过spearman计算出的自相关数值普遍高于pearson。

图13       PB因子的暴露度自相关性

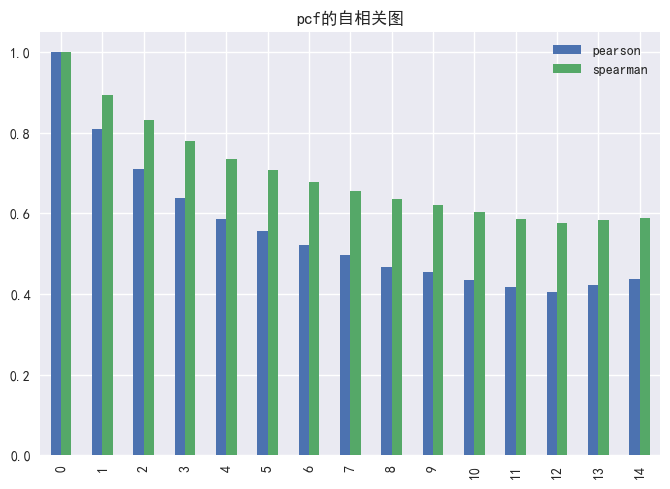
图14       PCF因子的暴露度自相关性

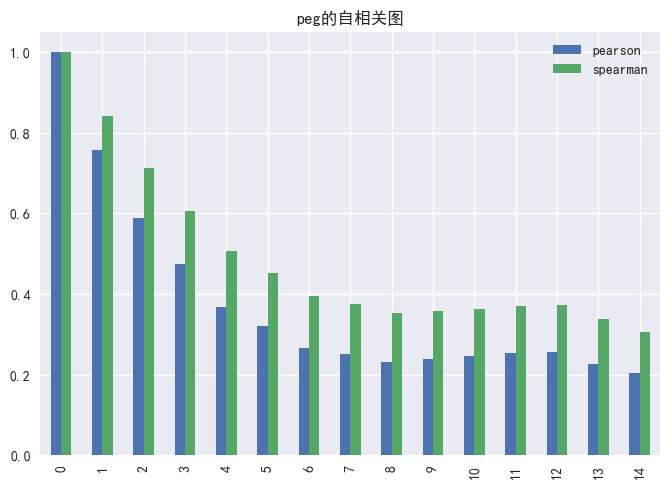
图15       PEG因子的暴露度自相关性

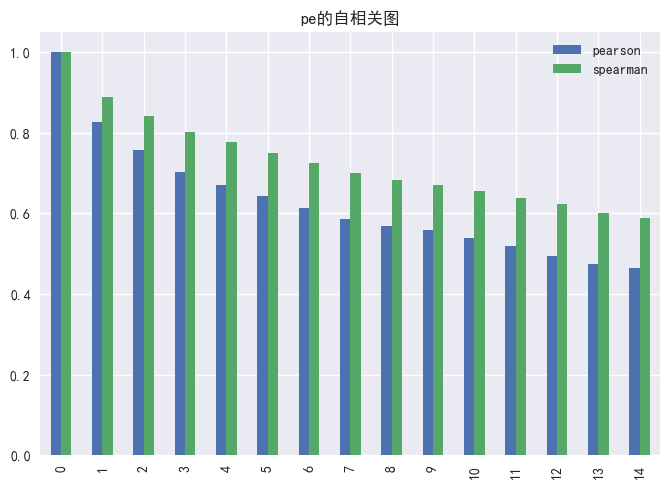
图16       PE因子的暴露度自相关性

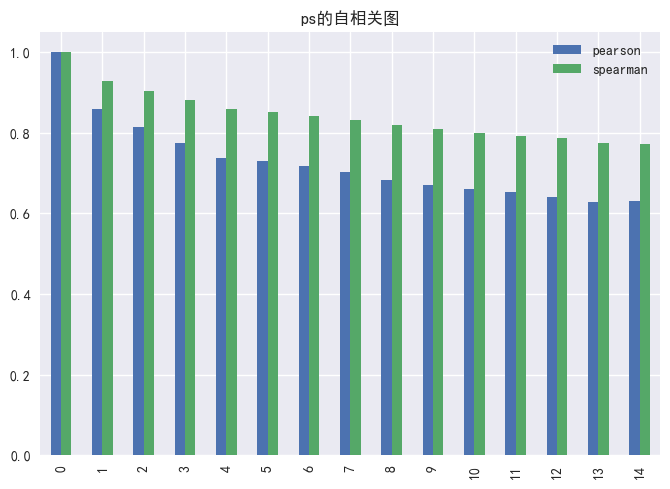
图17       PS因子的暴露度自相关性

四、因子有效性和稳定性的初步分析

IC：                                             股票的因子暴露度与下期股票收益率之间的pearson相关系数

RANK-IC：               股票的因子暴露度与下期股票收益率之间的spearman相关系数

IR：                                             对应相关系数（IC/RANK-IC）的均值与标准差的比值

其中IC和RANK-IC两种指标的计算逻辑存在以下不同：

IC                                                  主要衡量因子和收益率之间的线性关系，因子暴露度需要是正态的。

RANK-IC                    主要衡量分级定序之后因子和收益率之间的相关程度的统计量，因子暴露度不要求是正态分布的，即不对变量的分布做假设，当数据存在异常值的时候较适用，但是由于计算逻辑较复杂，耗费时间较长。

通过对比两类相关系数，一般来说，相关系数的绝对值越大，意味着因子预测预期收益率的能力越强，由于样本点的实际分布和正态分布相差较大，所以也计算了spearman秩相关系数，IC衡量线性相关程度，RANK-IC衡量顺序相关程度。

这篇报告的因子检验主要从稳定性和有效性两个角度进行诠释。

4．1   因子相关系数分析

4.1.1              因子的IC/RANK-IC统计量和分布

表2展示了因子IC和RANK-IC的统计量，包括因子IC均值，IC标准差，NORMAL-IR，RANK-IC均值，RANK-IC标准差，RANK-IR。

使用RANK-IC或者IC计算因子暴露度和收益率的相关系数，只在数值上存在细微区别， RANK-IC的平均值绝对值比IC的平均值绝对值大，RANK-IC的标准差也比IC的标准差大。

PE因子IC和RANK-IC均值的绝对值最大，但是其标准差也较大；PEG因子IC和RANK-IC的标准差最小，但其RANK-IC的均值较小；说明没有一个因子在有效性和稳定性两个方面都可以占据优势。

表2

	pb	pcf	pe	peg	ps
IC_均值	-0.005535	-0.014628	-0.021070	-0.015535	-0.006488
IC_标准差	0.102703	0.112144	0.118845	0.088213	0.103774
NORMAL-IR	-0.053892	-0.130439	-0.177289	-0.176106	-0.062524
RANK-IC_均值	-0.029581	-0.035256	-0.036488	-0.030907	-0.030721
RANK-IC_标准差	0.131510	0.175479	0.164859	0.130121	0.146307
RANK-IR	-0.224936	-0.200912	-0.221330	-0.237526	-0.209976

图18到27展示了因子IC/RANK-IC的分布直方图

PB、PEG这两个因子看出相关系数的分布大部分处于负半轴上。而对于PE、PS、PCF这三个因子，RANKIC和IC的分布在正负区域上分布并不存在很大的区别，说明这三个因子稳定性较弱。

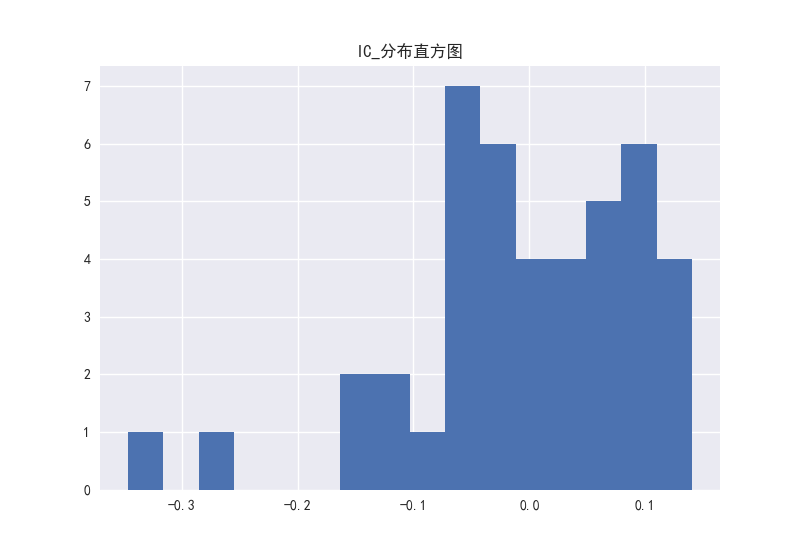
图18       PB因子的IC分布直方图

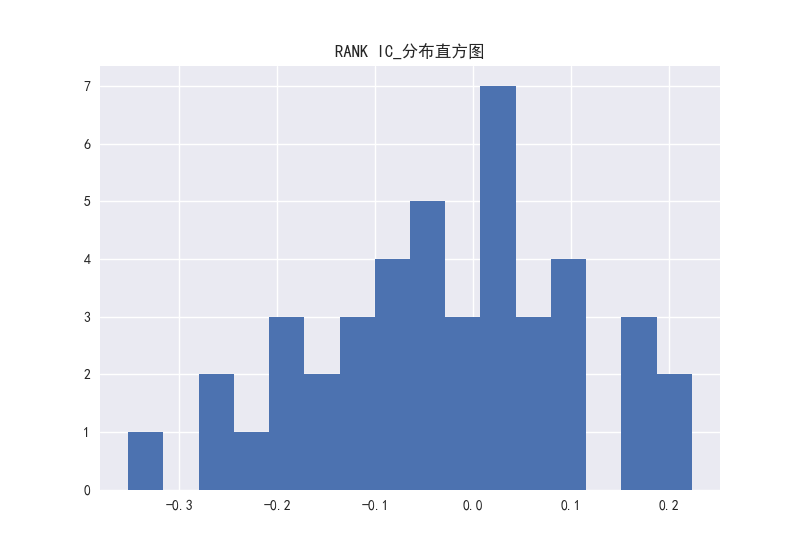
图19       PB因子的RANK-IC分布直方图

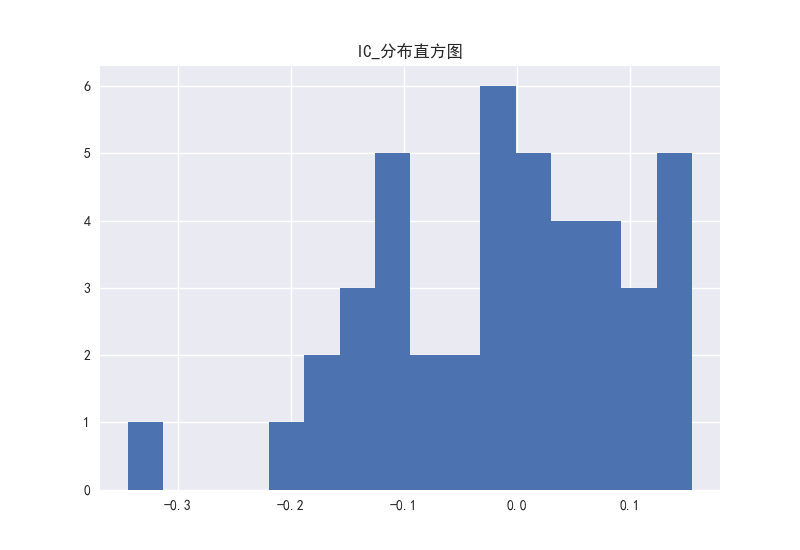
图20       PCF因子的IC分布直方图

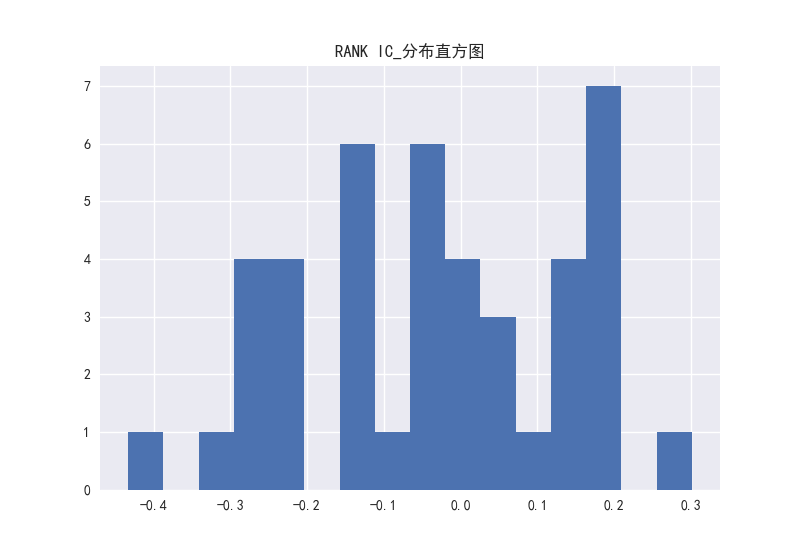
图21       PCF因子的RANK-IC分布直方图

图22       PE因子的IC分布直方图

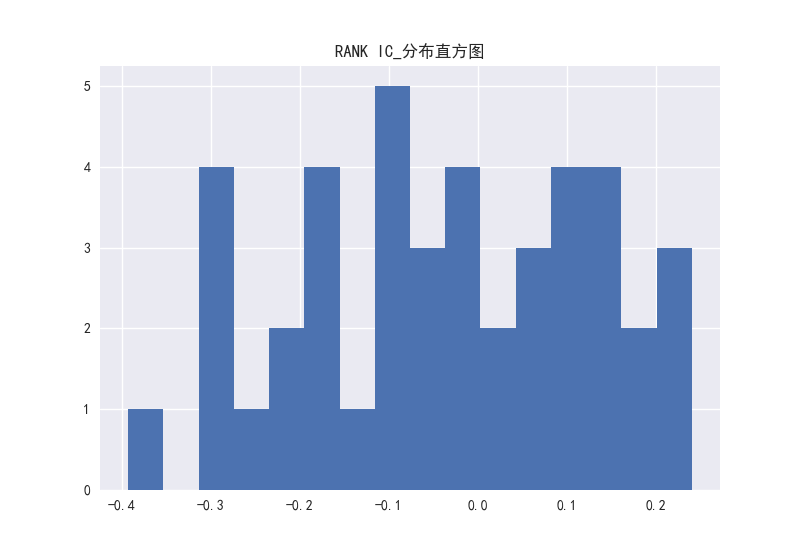
图23       PE因子的RANK-IC分布直方图

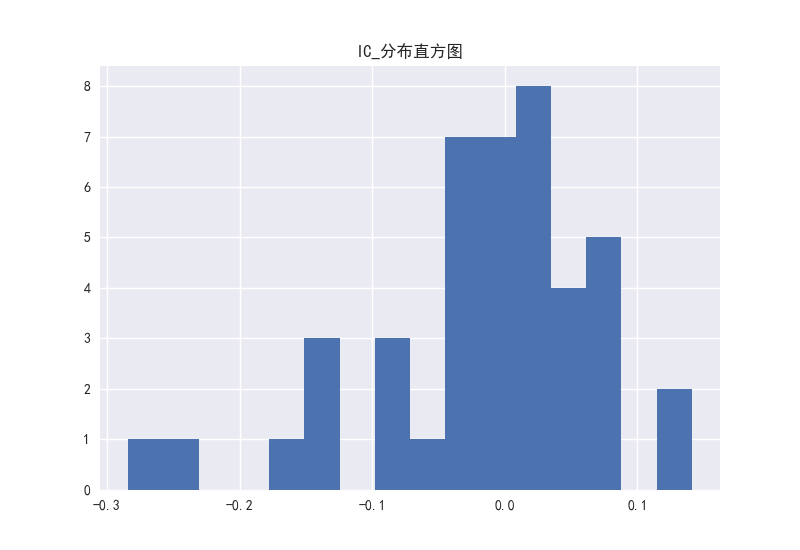
图24       PEG因子的IC分布直方图

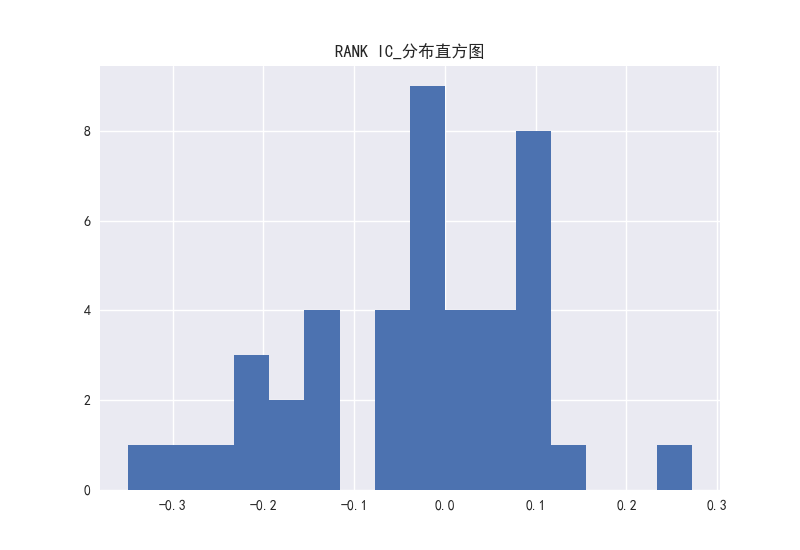
图25       PEG因子的RANK-IC分布直方图

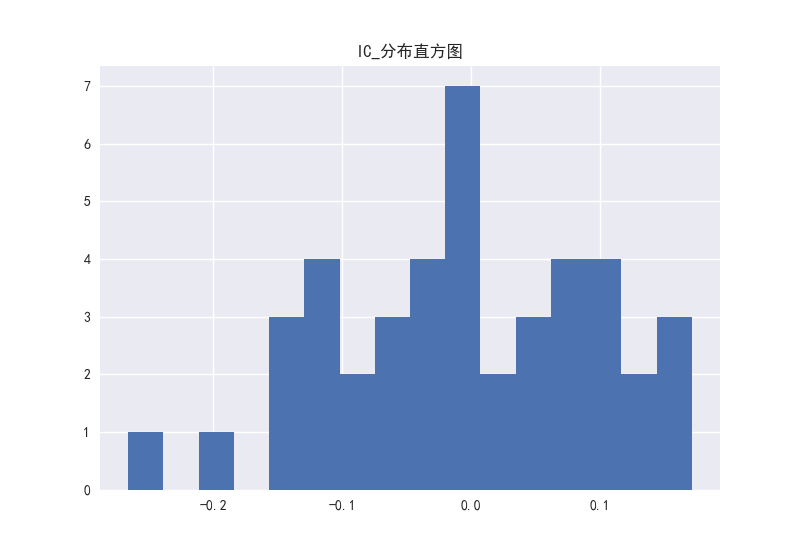
图26       PS因子的IC分布直方图

图27       PS因子的RANK-IC分布直方图

4.1.2              因子的IC/RANK-IC时间序列

图28到图42展示了因子IC/RANK-IC时间序列图，其中移动平均是窗口大小为6

图28和图29展示了PB因子在2015年到2016年之间的IC波动频繁，PB因子的暴露度在市场不稳定的时候波动较大，图29展示了PB因子的RANK-IC在2017年大部分都小于0，说明PB因子暴露度和收益率存在较明显的负相关趋势性。

图31和图32展示了PCF因子的移动平均在负半轴上的绝对值增大，PCF因子近期暴露度和收益率存在负相关趋势性。

图34和图35展示了PE因子的IC和RANK-IC的数值上较大。

图37和图38展示了PEG因子的移动平均值在负半轴上的绝对值增大，近期PEG因子相关性存在较强的负向趋势。

图40和图41展示了PS因子的IC和RANK-IC的波动频繁，可能存在噪音。

综合图30/33/36/39/42，在PB、PE、PCF、PS、PEG五个因子的大部分时间段，IC和RANKIC没有明显的差异，当相关系数在数量上增大的时候，RANKIC和IC的差异会扩大。

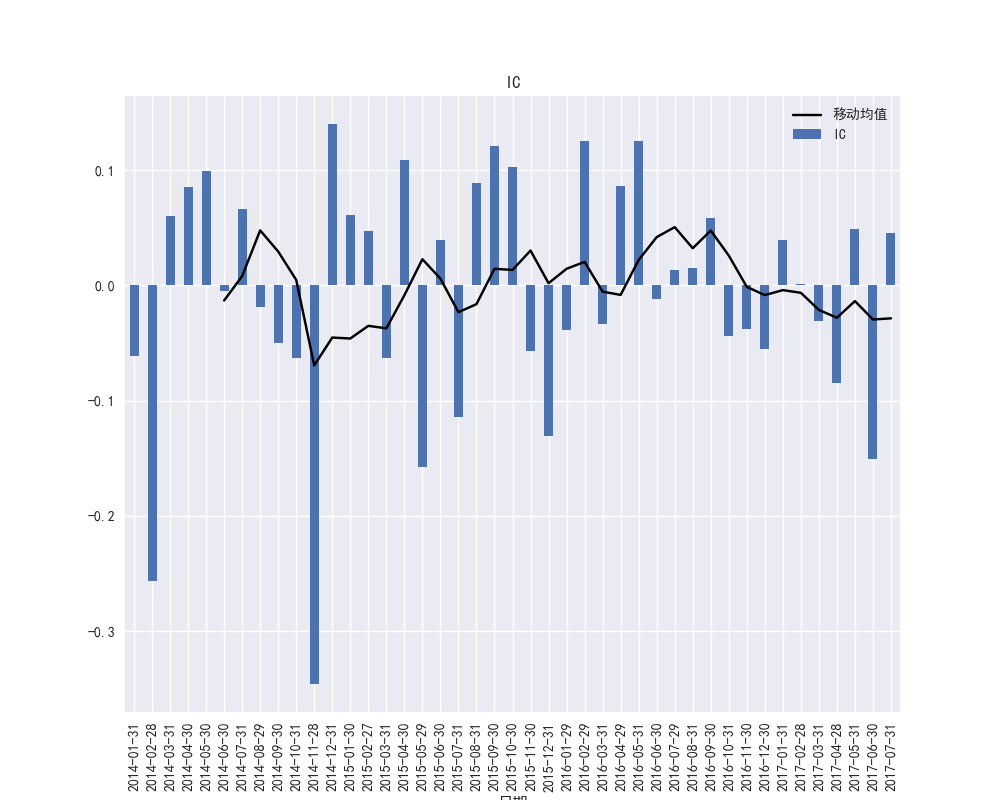
图28       PB因子的IC时间序列和IC的移动平均

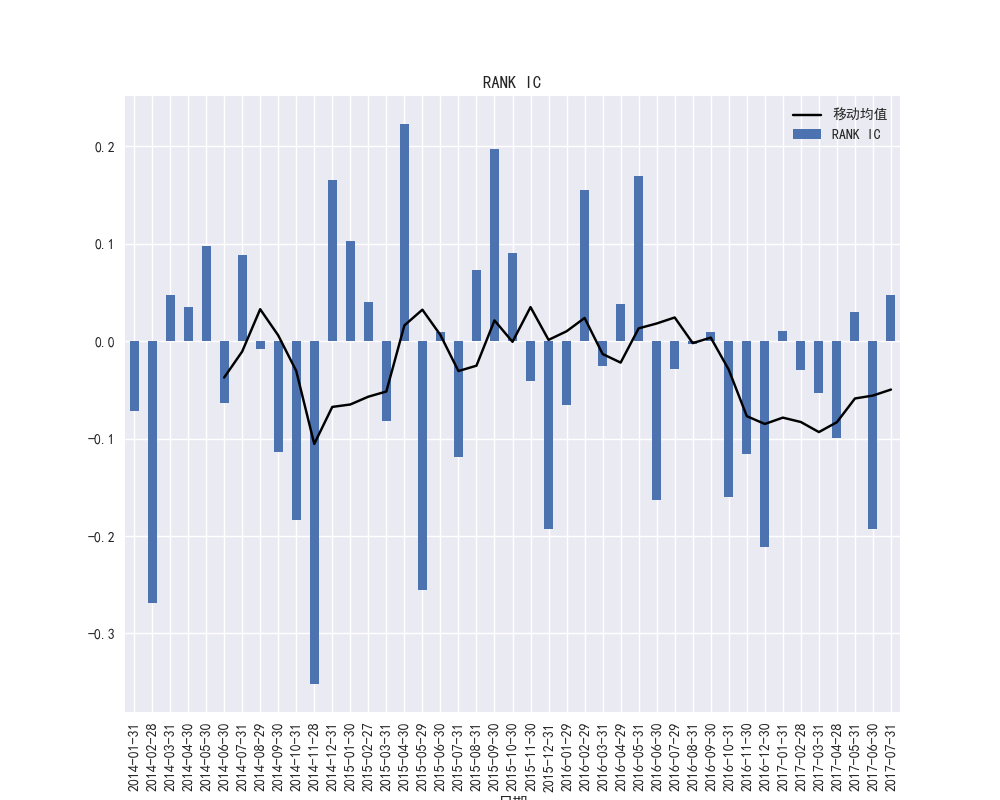
图29       PB因子的RANK-IC时间序列和RANK-IC的移动平均

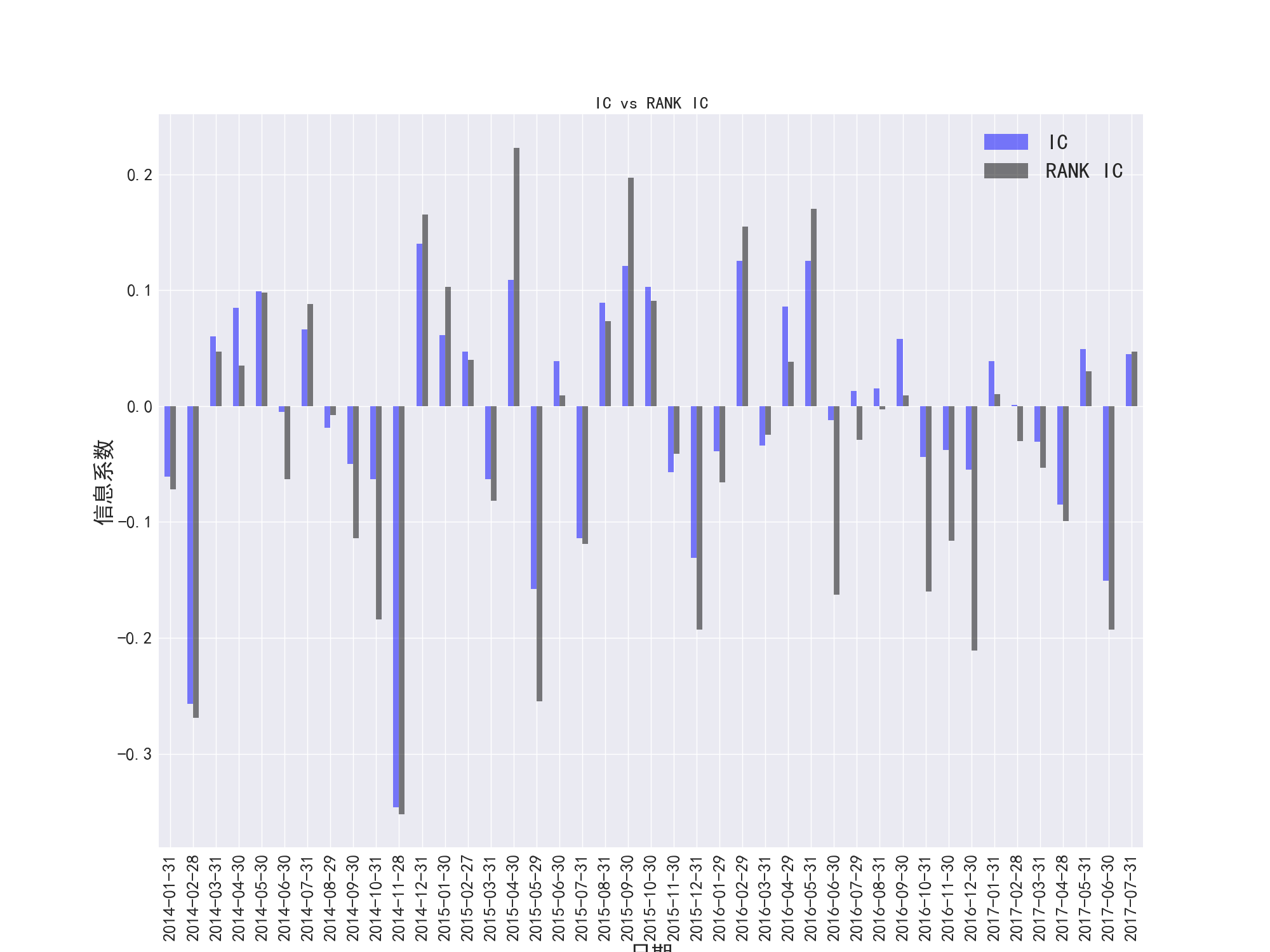
图30       PB因子的IC和RANK-IC对比

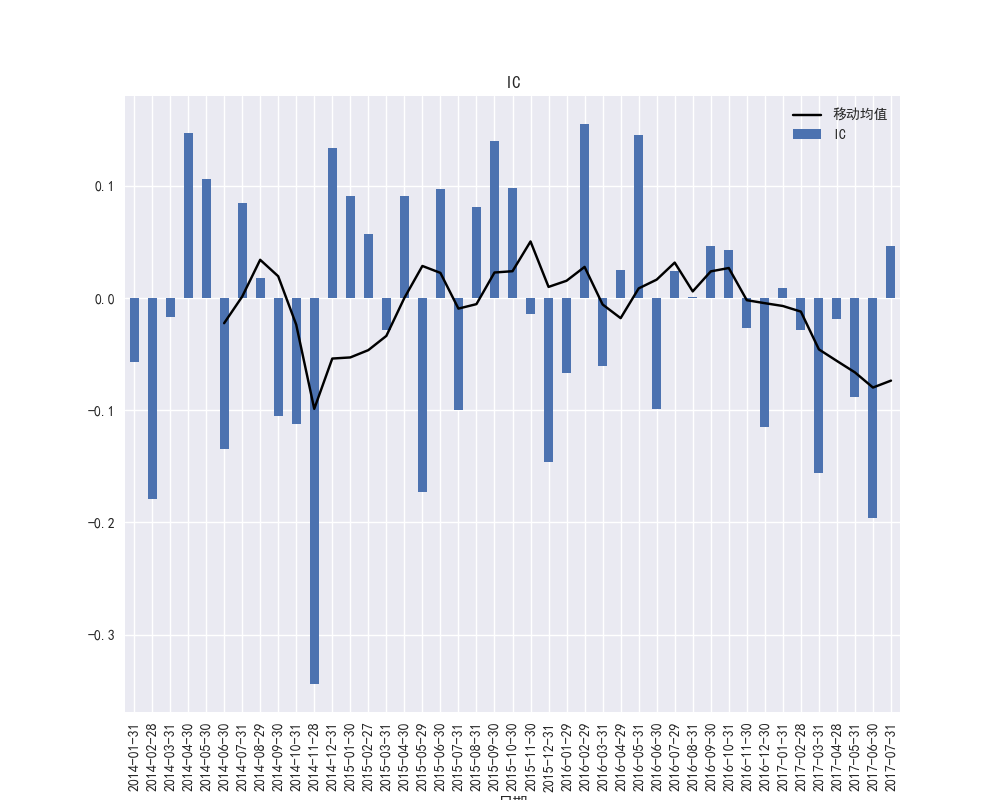
图31       PCF因子的IC时间序列和IC的移动平均

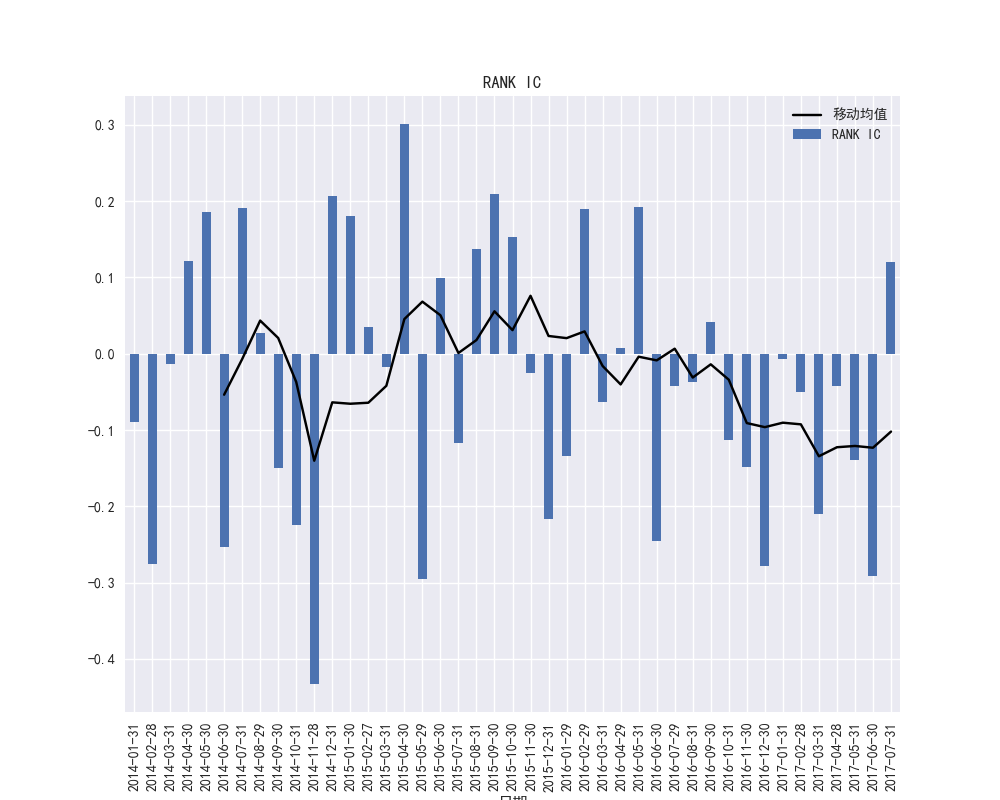
图32       PCF因子的RANK-IC时间序列和RANK-IC的移动平均

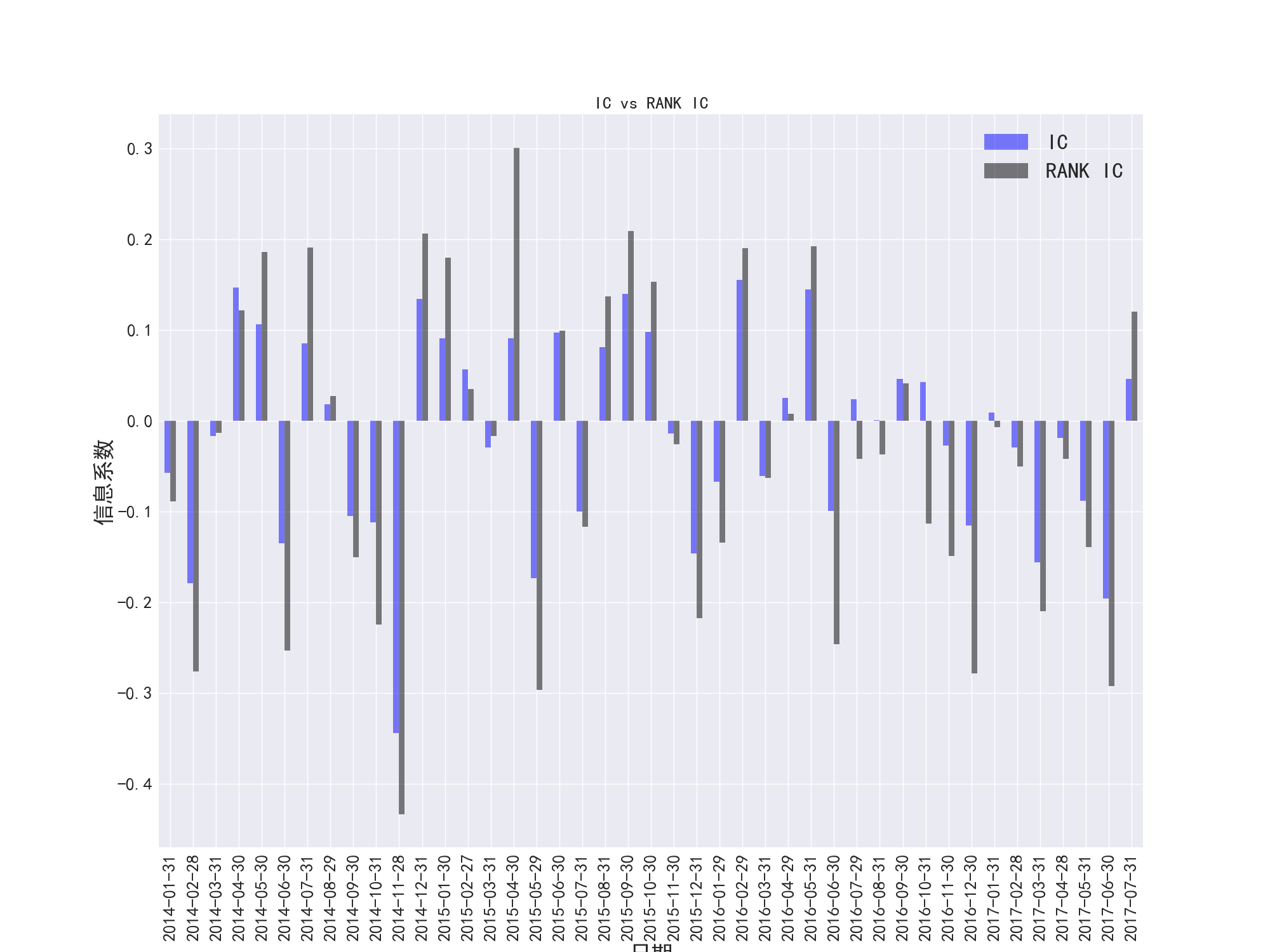
图33       PCF因子的IC和RANK-IC对比

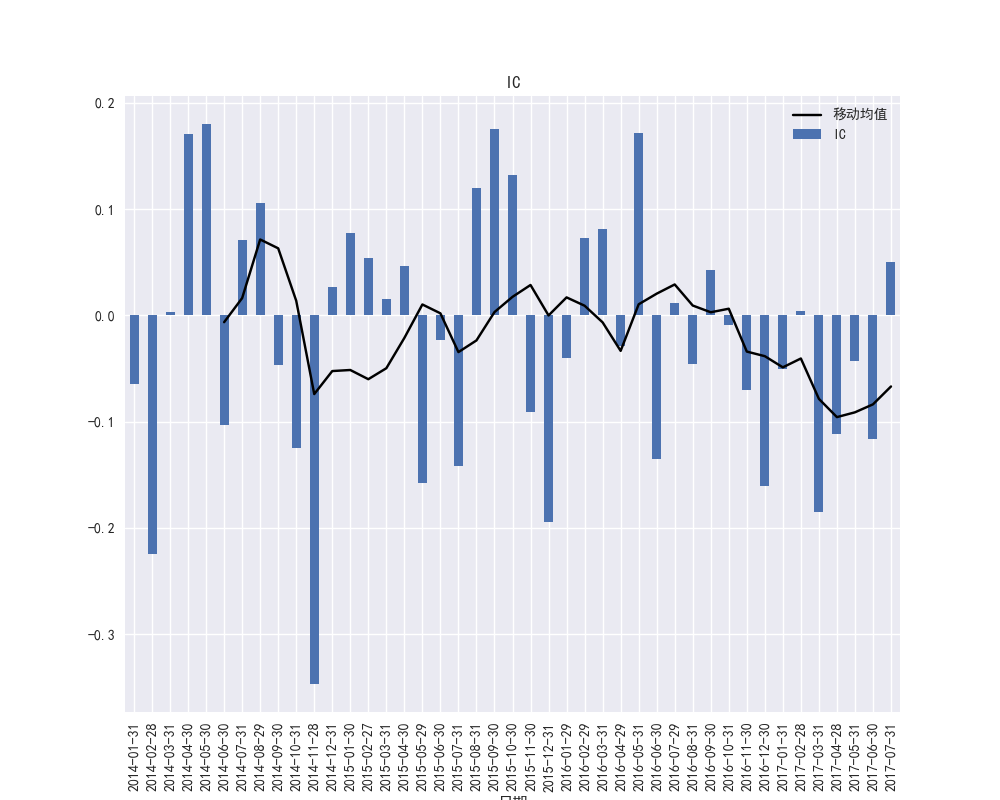
图34       PE因子的IC时间序列和IC的移动平均

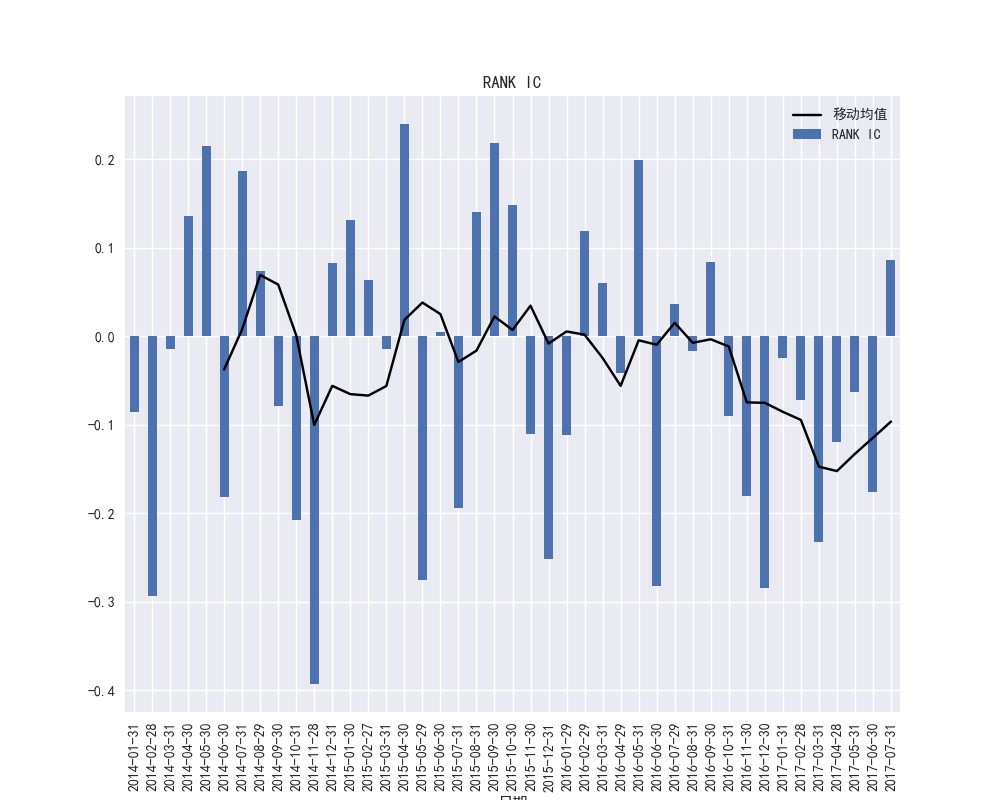
图35       PE因子的RANK-IC时间序列和RANK-IC的移动平均

图36       PE因子的IC和RANK-IC对比

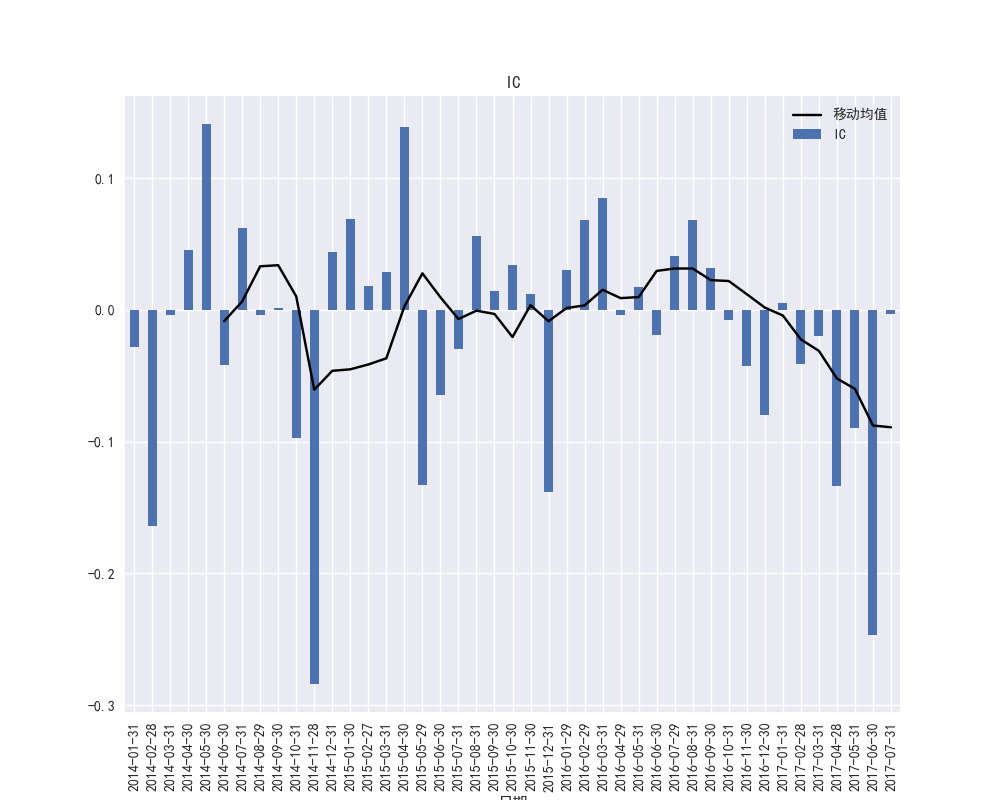
图37       PEG因子的IC时间序列和IC的移动平均

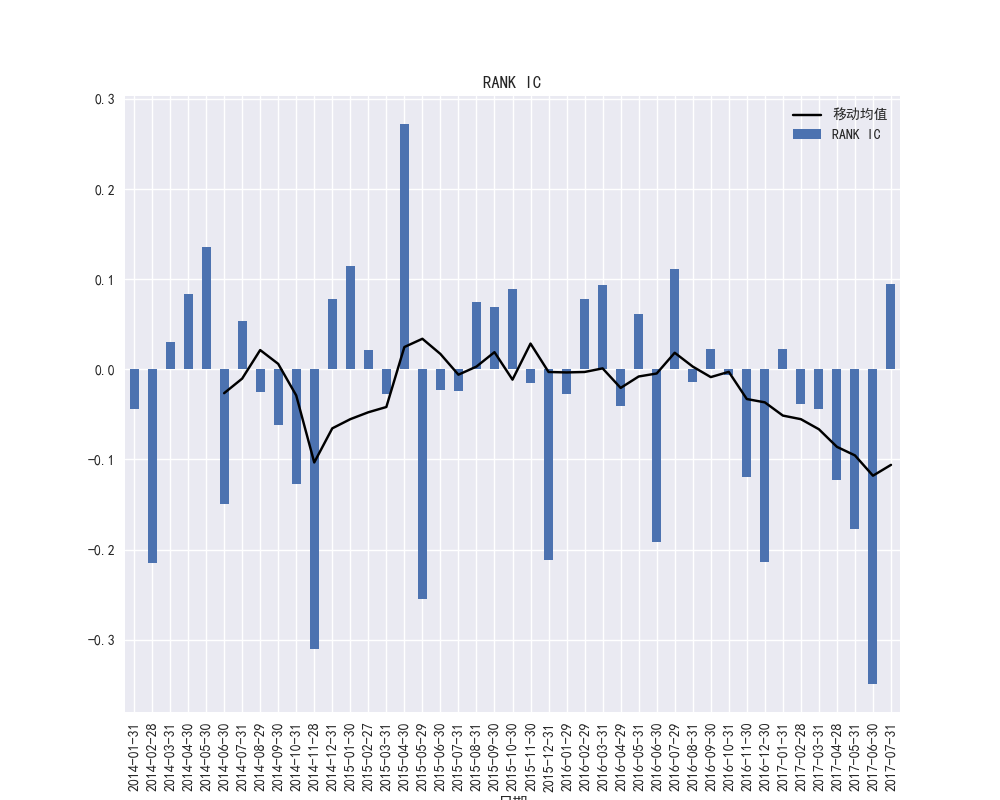
图38       PEG因子的RANK-IC时间序列和RANK-IC的移动平均

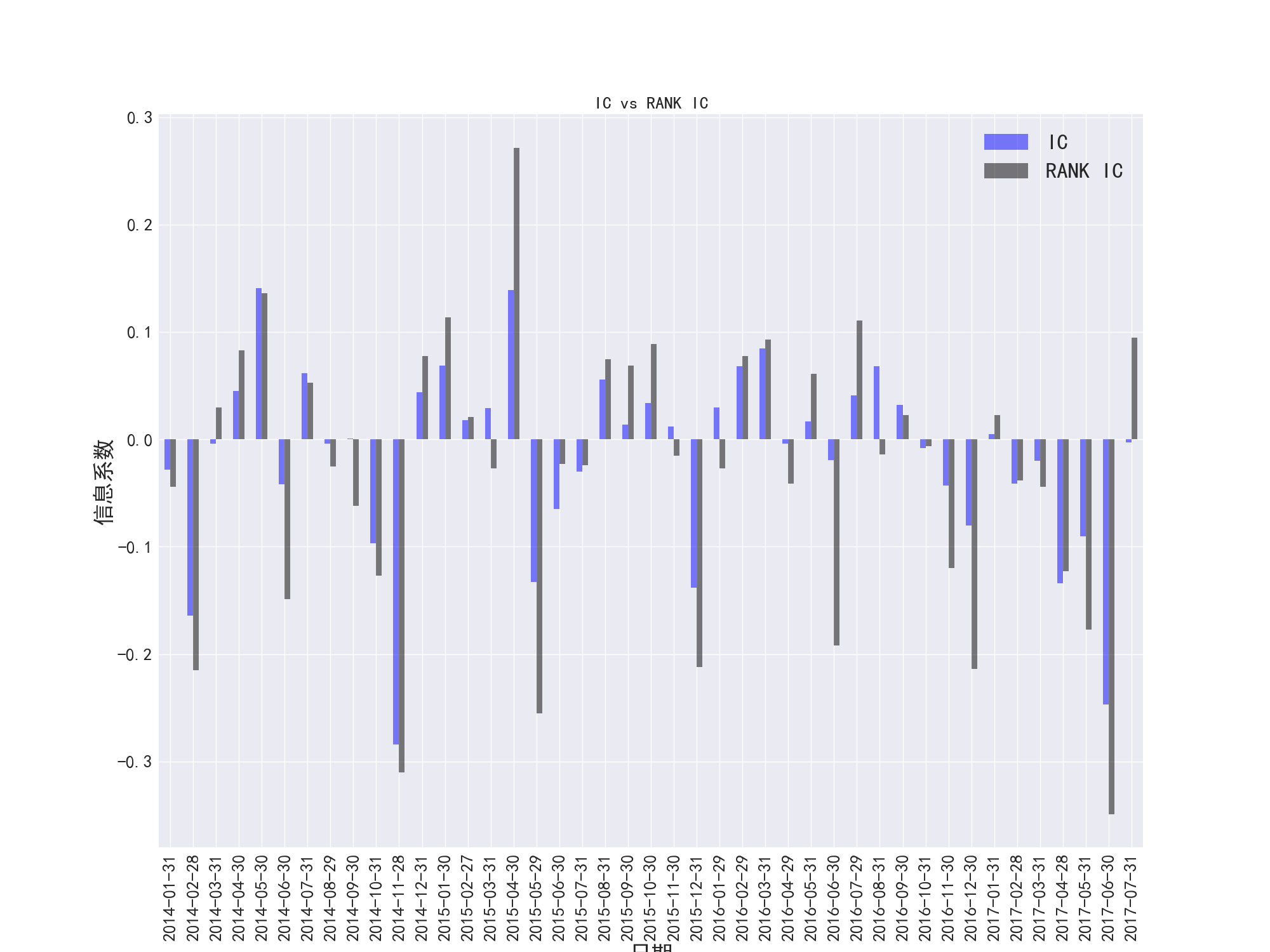
图39       PEG因子的IC和RANK-IC对比

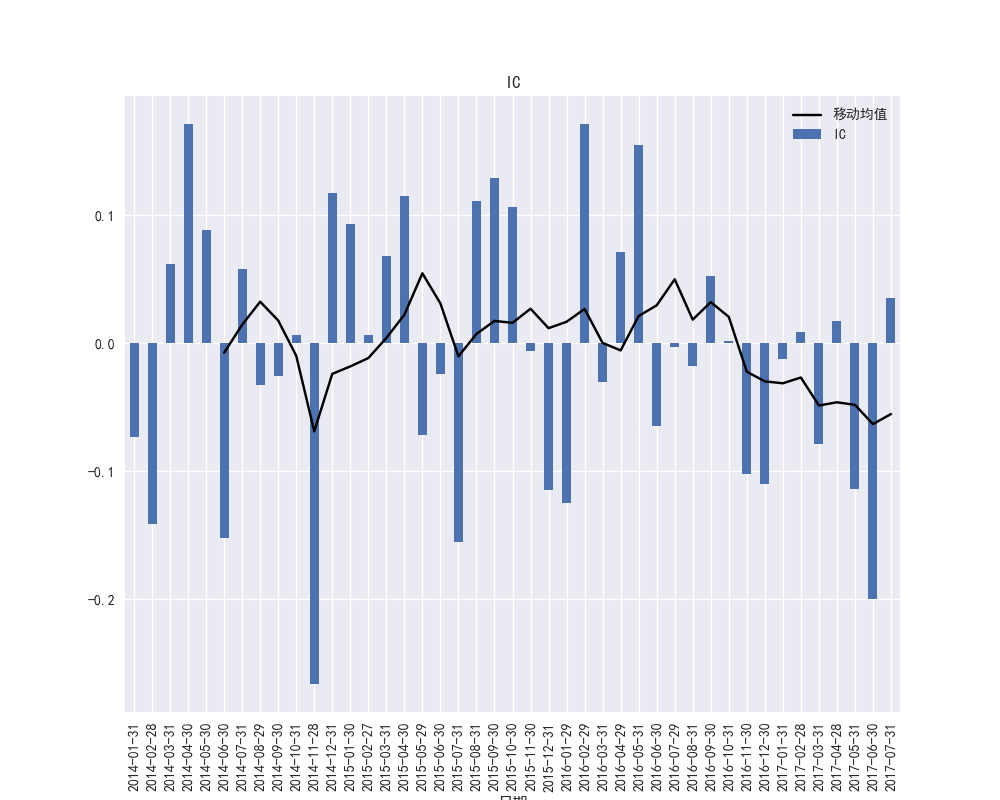
图40       PS因子的IC时间序列和IC的移动平均

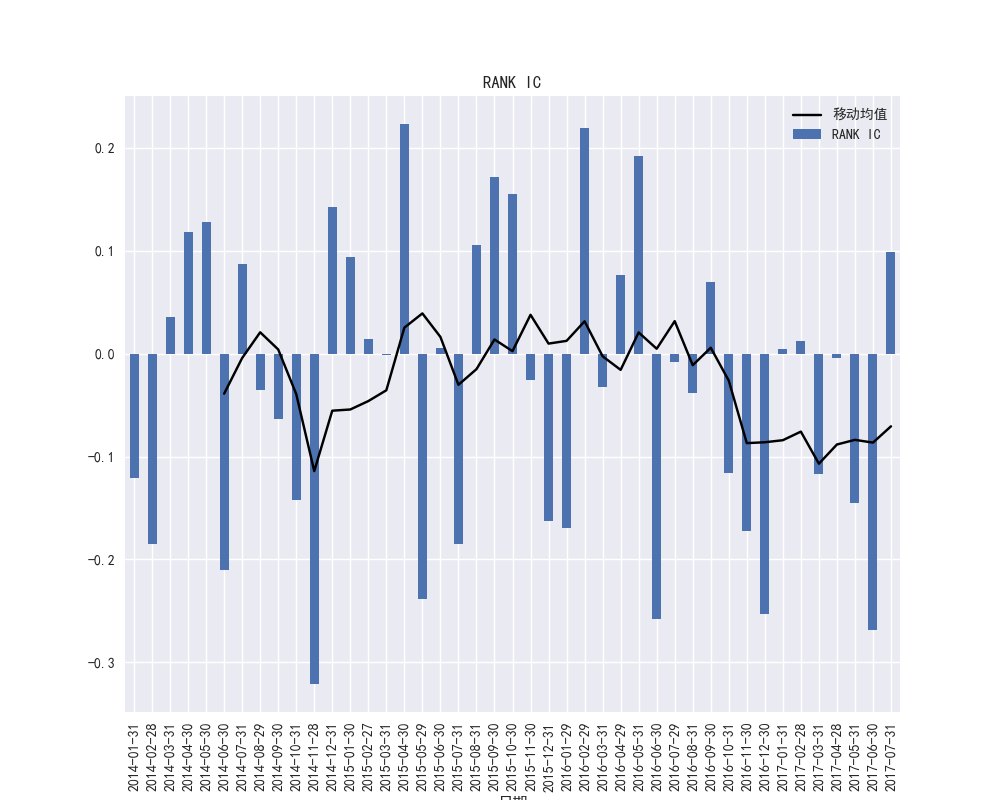
图41       PS因子的RANK-IC时间序列和RANK-IC的移动平均

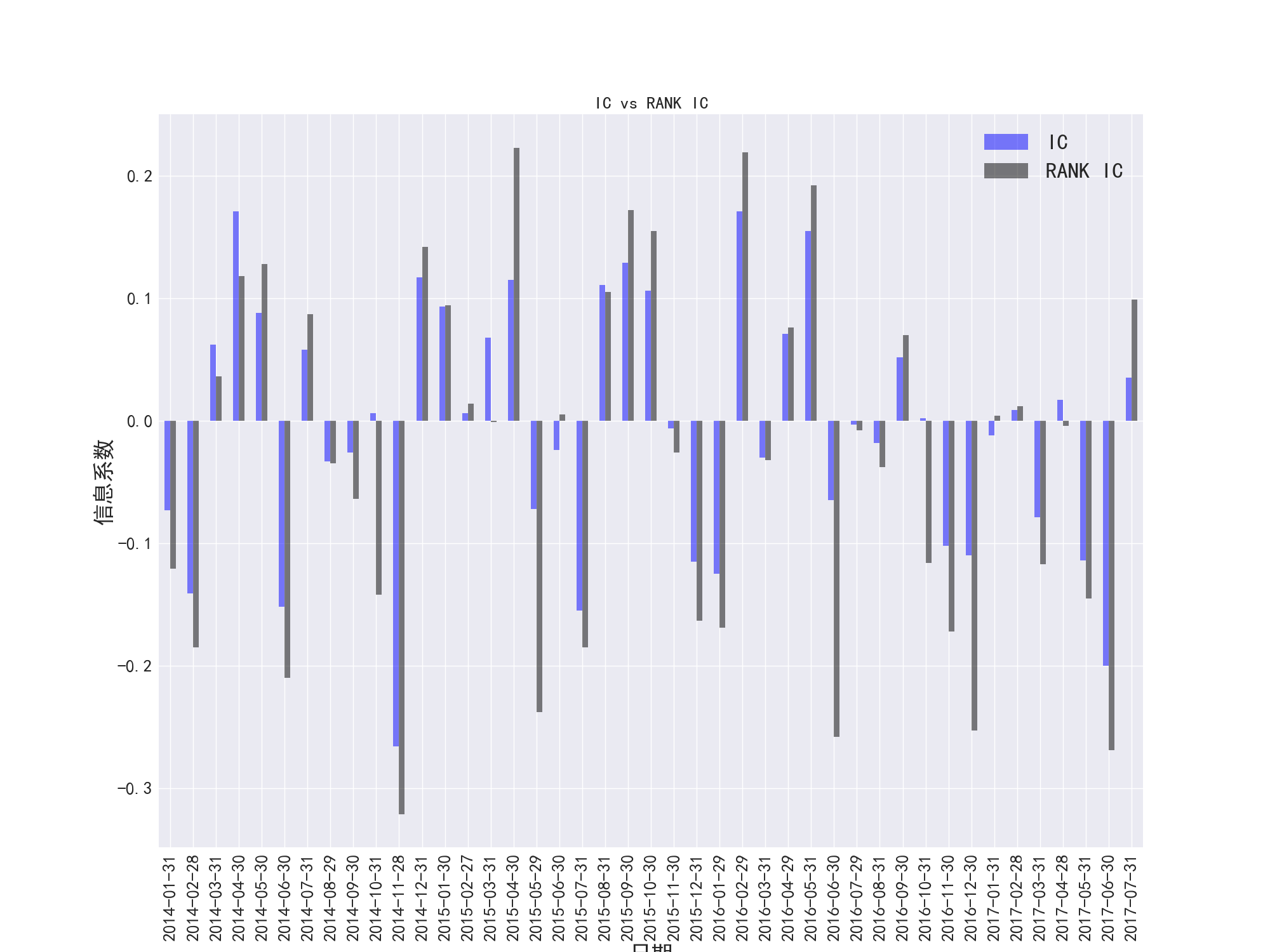
图42       PS因子的IC和RANK-IC对比

4．1.3   IC/RANK-IC相关的自定义比例指标

一般而言，市场风格不是一层不变的，而是轮动的，所以所求的IC或者RANK_IC的相关系数会存在符号上的切换，所以在选择因子的时候，一般是计算相关系数正负的比例，选择相关比例较高的一个方向作为因子在未来的预测方向。这里选择了正相关显著比例、负相关显著比例、同向显著比例和状态切换比例作为衡量因子方向的指标。

指标的相关定义如下：

显著：是指相关系数的显著性水平小于一定阈值的样本。

正相关显著比例：显著的正相关系数占样本的比例

负相关显著比例：显著的负相关系数占样本的比例

状态切换显著比例：前后两期中相关系数符号相反占样本的比例。

同向显著比例：前后两期中相关系数符号相同占样本的比例。

所以：假如同向显著比例占上风，则意味着该段时间内因子的风格延续性较强，可以使用动态权重来调整因子的权重；同理，如果状态切换比例占上风，对于因子的赋权应该使用静态权重。

以最近一年时间即2016年8月1日到2017年8月1日的因子数据为研究对象

图43、44展示了PE，PEG，PCF，PB，PS五个因子的IC显著的状态切换比例，同向显著比例，负相关比例，正相关比例。

可以看出PE因子的IC同向显著比例较高，并且IC负相关显著比例高，说明PE因子暴露度与收益率可能存在负相关关系，并且这种关系可能持续下去。

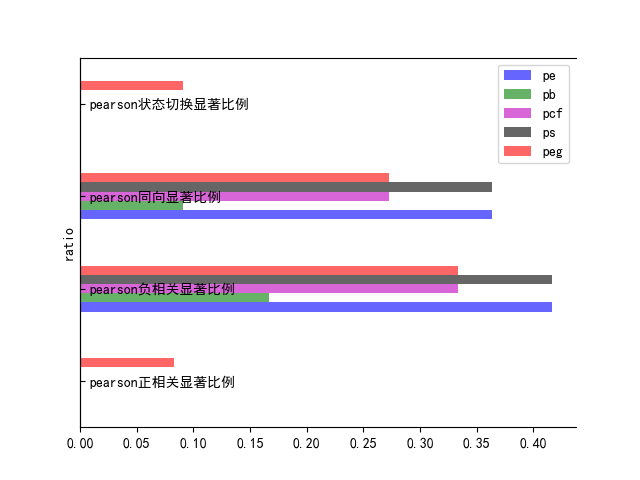
图43   IC自定义比例指标

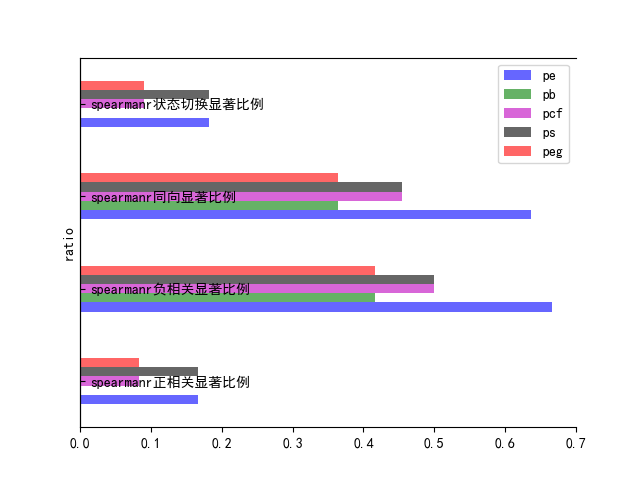
图44   RANK-IC自定义比例指标

4．1.4  IC/RANK-IC相关的自定义趋势指标和显著指标

此次报告衡量因子是否显著的标准有两个条件

1、相关系数的正负显著比例至少有一项大于阈值A，

2、相关系数的正负显著比例之和大于阈值B，

此次报告中阈值A
= 0.35，阈值B=
0.6

因子是否具有趋势性：

因子具有趋势性：同向显著比例大于显著状态切换比例

表3          IC/RANK-IC相关的趋势/显著指标

指标	pe	pb	pcf	ps	peg
pearson相关比例是否显著	负相关比例显著	正负相关比例均不显著	正负相关比例均不显著	负相关比例显著	正负相关比例均不显著
pearson正负相关比例之和是否显著	False	False	False	False	False
pearson_趋势性	True	False	True	False	True
spearmanr相关比例是否显著	负相关比例显著	负相关比例显著	负相关比例显著	负相关比例显著	负相关比例显著
spearmanr正负相关比例之和是否显著	True	False	False	True	False
spearmanr_趋势性	True	False	True	True	True

4.2收益率分析

图45展示了PB因子第四组分组收益累计最高，其他几组之间没有显著差异，并且这种差异是从2016年开始显现出来的，说明最近一年的暴露度和收益的相关关系可能出现反转。观察PB因子的IC时间序列图也可以看出IC在2016年开始转为正值。

图46展示了PCF可以看出在牛市第一组和第四组因子组合可以获得快速上涨的收益，而第三组表现最差。通过对比IC和RANK-IC的时间序列在2015年移动均值的绝对值有减小的趋势，说明暴露度和收益率的相关系数出现波动，也说明了PCF的稳定性减弱。

图47展示了PE因子的第一组和第三组累计收益较高，两者之间没有显著差异，这种差异从2015年开始显现出来，RANK-IC时间序列的移动平均值从2015年之后大部分处于小于零的部分，说明第一、三组和其他几组的累计收益的差异有可能扩大。

图48展示了PEG的因子累计收益其他几组没有显著差异，第4组表现较差。

图49展示了PS因子第三组累计收益最低，并且这种差异从2015年开始； IC和RANK-IC的移动平均值在2015年位于零值附近波动，说明因子暴露度和收益率之间没有固定的相关方向，PS因子在牛市和股灾期间的稳定性较差。

综上所述PB、PS、PE、PEG、PCF因子暴露度与收益没有线性关系。

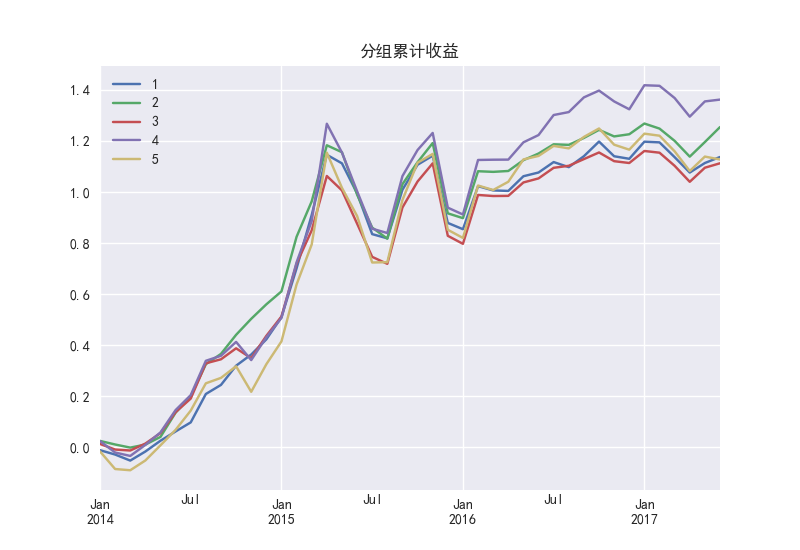
图 45                         PB因子的分组累计收益

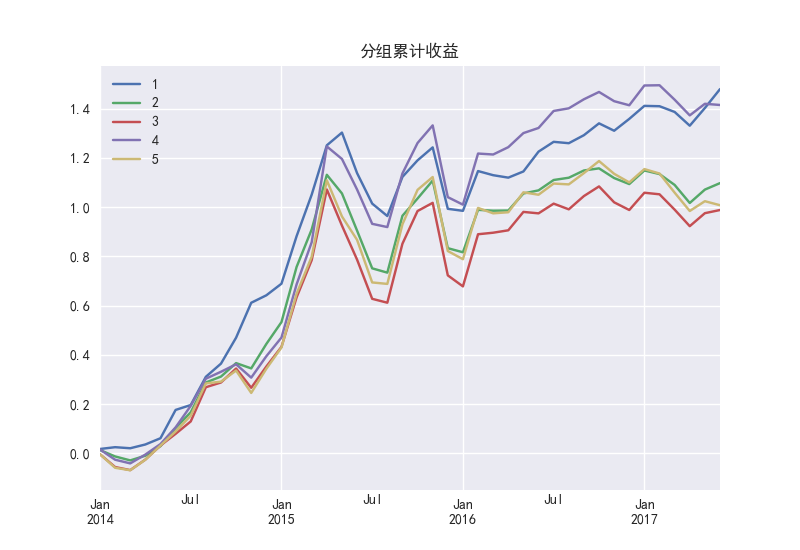
图 46                         PCF因子的分组累计收益

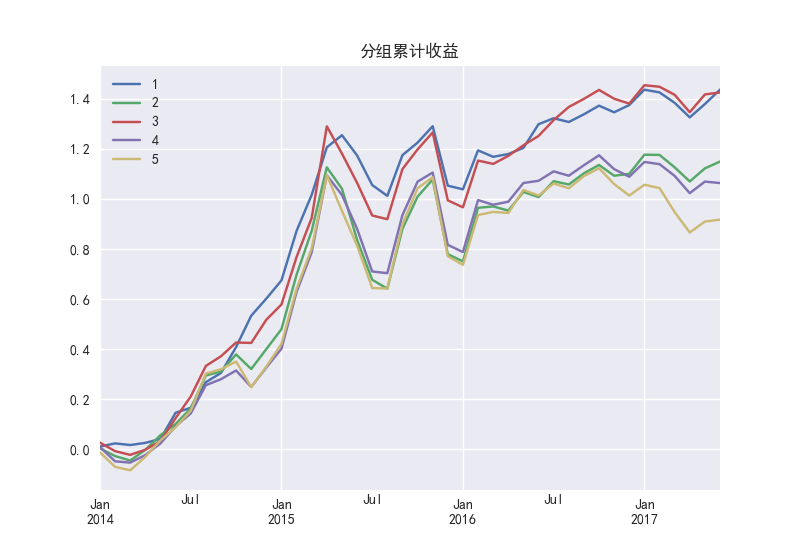
图47                         PE因子的分组累计收益

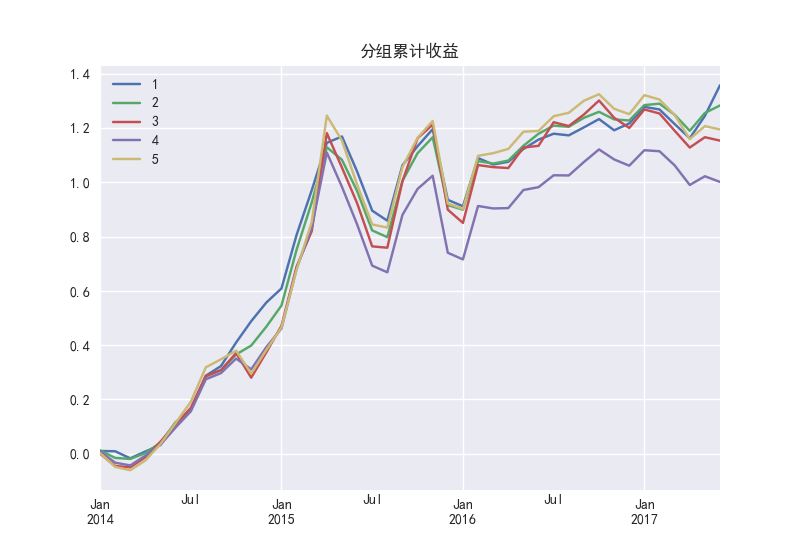
图48                         PEG因子的分组累计收益

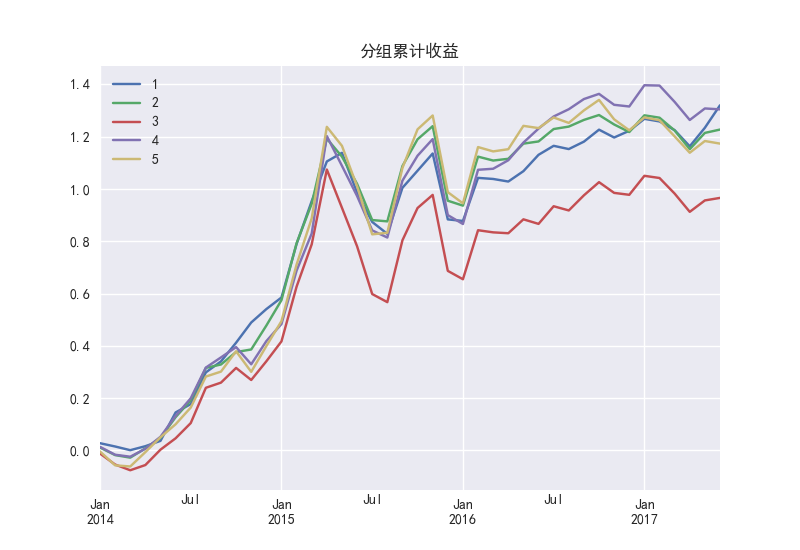
图 49                         PS因子的分组累计收益

五、小结

通过上面的分析可以得出以下结论：

1、  此次所选的五个因子与收益率在长期上都存在负相关关系

2、  在时间序列上，PEG因子的暴露度相对其他因子较为稳定，在近一年表现出较强的趋势性

3、  PE因子的负相关性比较显著，并且有一定的趋势性，通过观察RANK-IC的同向显著比例和负相关显著比例，PE因子可能比其他因子更加有负向的趋势性，稳定性更好

4、  PB因子的分布有明显的左偏，并且分布比较规范，但是稳定性表现一般。

5、  PCF、PS因子近期的稳定性和有效性表现一般