AdaBoost原理详解

写一点自己理解的AdaBoost，然后再贴上面试过程中被问到的相关问题。按照以下目录展开。

当然，也可以去我的博客上看

Boosting提升算法
AdaBoost
- 原理理解
- 实例
- 算法流程
- 公式推导
面经

Boosting提升算法

AdaBoost是典型的Boosting算法，属于Boosting家族的一员。在说AdaBoost之前，先说说Boosting提升算法。Boosting算法是将“弱学习算法“提升为“强学习算法”的过程，主要思想是“三个臭皮匠顶个诸葛亮”。一般来说，找到弱学习算法要相对容易一些，然后通过反复学习得到一系列弱分类器，组合这些弱分类器得到一个强分类器。Boosting算法要涉及到两个部分，加法模型和前向分步算法。加法模型就是说强分类器由一系列弱分类器线性相加而成。一般组合形式如下：

$$F_M(x;P)=\sum_{m=1}^nβ_mh(x;a_m)$$

其中，$h(x;a_m)$ 就是一个个的弱分类器，$a_m$是弱分类器学习到的最优参数，$β_m$就是弱学习在强分类器中所占比重，$P$是所有$a_m$和$β_m$的组合。这些弱分类器线性相加组成强分类器。

前向分步就是说在训练过程中，下一轮迭代产生的分类器是在上一轮的基础上训练得来的。也就是可以写成这样的形式：

$$F_m (x)=F_{m-1}(x)+ β_mh_m (x;a_m)$$

由于采用的损失函数不同，Boosting算法也因此有了不同的类型，AdaBoost就是损失函数为指数损失的Boosting算法。

AdaBoost

原理理解

基于Boosting的理解，对于AdaBoost，我们要搞清楚两点：

每一次迭代的弱学习$h(x;a_m)$有何不一样，如何学习？
弱分类器权值$β_m$如何确定？

对于第一个问题，AdaBoost改变了训练数据的权值，也就是样本的概率分布，其思想是将关注点放在被错误分类的样本上，减小上一轮被正确分类的样本权值，提高那些被错误分类的样本权值。然后，再根据所采用的一些基本机器学习算法进行学习，比如逻辑回归。

对于第二个问题，AdaBoost采用加权多数表决的方法，加大分类误差率小的弱分类器的权重，减小分类误差率大的弱分类器的权重。这个很好理解，正确率高分得好的弱分类器在强分类器中当然应该有较大的发言权。

实例

为了加深理解，我们来举一个例子。

有如下的训练样本，我们需要构建强分类器对其进行分类。x是特征，y是标签。

序号	1	2	3	4	5	6	7	8	9	10
x	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1

令权值分布$D_1=(w_{1,1},w_{1,2},…,w_{1,10} )$

并假设一开始的权值分布是均匀分布：$w_{1,i}=0.1，i=1,2,…,10$

现在开始训练第一个弱分类器。我们发现阈值取2.5时分类误差率最低，得到弱分类器为：

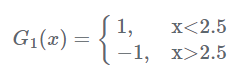
当然，也可以用别的弱分类器，只要误差率最低即可。这里为了方便，用了分段函数。得到了分类误差率$e_1=0.3$。

第二步计算$(G_1 (x)$在强分类器中的系数$α_1=\frac{1}{2} log\frac{ 1-e_1}{e_1}=0.4236$，这个公式先放在这里，下面再做推导。

第三步更新样本的权值分布，用于下一轮迭代训练。由公式：

$$w_{2,i}=\frac{w_{1,i}}{z_1}exp⁡(-α_1 y_i G_1 (x_i ))，i=1,2,…,10$$

得到新的权值分布，从各0.1变成了:

$$D_2=(0.0715,0.0715,0.0715,0.0715,0.0715,0.0715,0.1666,0.1666,0.1666,0.0715)$$

可以看出，被分类正确的样本权值减小了，被错误分类的样本权值提高了。

第四步得到第一轮迭代的强分类器：

$$sign(F_1 (x))=sign(0.4236G_1 (x))$$

以此类推，经过第二轮……第N轮，迭代多次直至得到最终的强分类器。迭代范围可以自己定义，比如限定收敛阈值，分类误差率小于某一个值就停止迭代，比如限定迭代次数，迭代1000次停止。这里数据简单，在第3轮迭代时，得到强分类器：

$$sign(F_3 (x))=sign(0.4236G_1 (x)+0.6496G_2 (x)+0.7514G_3 (x))$$
的分类误差率为0，结束迭代。

$F(x)=sign(F_3 (x))$就是最终的强分类器。

算法流程

总结一下，得到AdaBoost的算法流程：

输入：训练数据集$T=\{(x_1,y_1),(x_2,y_2),(x_N,y_N)\}$，其中，$x_i∈X⊆R^n$，$y_i∈Y={-1,1}$，迭代次数$M$
1.　初始化训练样本的权值分布：$D_1=(w_{1,1},w_{1,2},…,w_{1,i}),w_{1,i}=\frac{1}{N},i=1,2,…,N$。
2.　对于$m=1,2,…,M$
　　(a)　使用具有权值分布$D_m$的训练数据集进行学习，得到弱分类器$G_m (x)$
　　(b)　计算$G_m(x)$在训练数据集上的分类误差率：

$$e_m=\sum_{i=1}^Nw_{m,i} I(G_m (x_i )≠y_i )$$

$$α_m=\frac{1}{2}log \frac{1-e_m}{e_m} $$

　　(d)　更新训练数据集的权值分布（这里，$z_m$是归一化因子，为了使样本的概率分布和为1）：

$$w_{m+1,i}=\frac{w_{m,i}}{z_m}exp⁡(-α_m y_i G_m (x_i ))，i=1,2,…,10$$

$$z_m=\sum_{i=1}^Nw_{m,i}exp⁡(-α_m y_i G_m (x_i ))$$

3. 得到最终分类器：

$$F(x)=sign(\sum_{i=1}^Nα_m G_m (x))$$

公式推导

现在我们来搞清楚上述公式是怎么来的。

假设已经经过$m-1$轮迭代，得到$F_{m-1} (x)$，根据前向分步，我们可以得到：

$$F_m (x)=F_{m-1} (x)+α_m G_m (x)$$

我们已经知道AdaBoost是采用指数损失，由此可以得到损失函数：

$$Loss=\sum_{i=1}^Nexp⁡(-y_i F_m (x_i ))=\sum_{i=1}^Nexp⁡(-y_i (F_{m-1} (x_i )+α_m G_m (x_i )))$$

这时候，$F_{m-1}(x)$是已知的，可以作为常量移到前面去:

$$Loss=\sum_{i=1}^N\widetilde{w_{m,i}} exp⁡(-y_i α_m G_m (x_i ))$$
其中，$\widetilde{w_{m,i}}=exp⁡(-y_i (F_{m-1} (x)))$ ，敲黑板！这个就是每轮迭代的样本权重！依赖于前一轮的迭代重分配。

是不是觉得还不够像？那就再化简一下：

$$\widetilde{w_{m,i}}=exp⁡(-y_i (F_{m-1} (x_i )+α_{m-1} G_{m-1} (x_i )))=\widetilde{w_{m-1,i}} exp⁡(-y_i α_{m-1} G_{m-1} (x_i ))$$

现在够像了吧？ok，我们继续化简Loss：

$$Loss=\sum_{y_i=G_m(x_i)}\widetilde{w_{m,i}} exp(-α_m)+\sum_{y_i≠G_m(x_i)}\widetilde{w_{m,i}} exp⁡(α_m)$$

$$=\sum_{i=1}^N\widetilde{w_{m,i}}(\frac{\sum_{y_i=G_m(x_i)}\widetilde{w_{m,i}}}{\sum_{i=1}^N\widetilde{w_{m,i}}}exp(-α_m)+\frac{\sum_{y_i≠G_m(x_i)}\widetilde{w_{m,i}}}{\sum_{i=1}^N\widetilde{w_{m,i}}}exp(α_m))$$

公式变形之后，炒鸡激动！$\frac{\sum_{y_i≠G_m(x_i)}\widetilde{w_{m,i}}}{\sum_{i=1}^N\widetilde{w_{m,i}}}$这个不就是分类误差率$e_m$吗？？？！重写一下，

$$Loss=\sum_{i=1}^N\widetilde{w_{m,i}}exp⁡(-α_m)+e_m exp⁡(α_m))$$

Ok，这样我们就得到了化简之后的损失函数。接下来就是求导了。

对$α_m$求偏导，令$\frac{∂Loss}{∂α_m }=0$得到：

$$α_m=\frac{1}{2}log\frac{1-e_m}{e_m} $$

真漂亮！

另外，AdaBoost的代码实战与详解请戳代码实战之AdaBoost

面经

今年8月开始找工作，参加大厂面试问到的相关问题有如下几点：

手推AdaBoost
与GBDT比较
AdaBoost几种基本机器学习算法哪个抗噪能力最强，哪个对重采样不敏感？

作者 Scorpio.Lu
转载请注明出处！