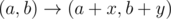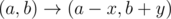Codeforces 817

A

你可以按如下方式移动

• 
• 
• 
• 

问能不能从给定的一个坐标走到另一个。

【solution】

裸，奇偶性注意

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
#include<map>
#include<vector>
#include<set>
#define il inline
#define re register
using namespace std;
int a1,b1,a2,b2,x,y,a,b;
int main(){
    cin>>a1>>b1>>a2>>b2>>x>>y;
    if((a1-a2)%x==&&(b1-b2)%y==){
        a=(a1-a2)/x;
        b=(b1-b2)/y;
        if((a-b)%==){
            cout<<"YES\n";
        }
        else cout<<"NO\n";
    }
    else cout<<"NO\n";
    return ;
}

B

After returning from the army Makes received a gift — an array a consisting of n positive integer numbers. He hadn't been solving problems for a long time, so he became interested to answer a particular question: how many triples of indices (i,  j,  k) (i < j < k), such that ai·aj·ak is minimum possible, are there in the array? Help him with it!

Input

The first line of input contains a positive integer number n (3 ≤ n ≤ 105) — the number of elements in array a. The second line contains n positive integer numbers ai (1 ≤ ai ≤ 109) — the elements of a given array.

Output

Print one number — the quantity of triples (i,  j,  k) such that i,  j and k are pairwise distinct and ai·aj·ak is minimum possible.

【solution】

就是问成绩最小的有序三元组有多少个，排序搞定

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
#include<map>
#include<vector>
#include<set>
#define il inline
#define re register
using namespace std;
typedef long long ll;
const int N=;
int n,a[N],b[N],c[N],m;
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%d",&a[i]);b[i]=a[i];
    }
    sort(b+,b+n+);
    m=unique(b+,b+n+)-b-;
    for(int i=;i<=n;i++)
        a[i]=lower_bound(b+,b+m+,a[i])-b;
    for(int i=;i<=n;i++) c[a[i]]++;
    if(c[]>=){
        cout<<((ll)c[]*(c[]-)*(c[]-)/)<<endl;
    }
    else{
        if(c[]==){
            cout<<c[]<<endl;
        }
        else if(c[]==){
            if(c[]>=) cout<<((ll)c[]*(c[]-)/)<<endl;
            else cout<<c[]<<endl;
        }
    }
    return ;
}

C

f(i)表示i所有数位的和

问满足 i-f(i)>=s  (i<=n) 的有多少个

n,s<=10^18

【solution】

显而易见，f(i)最大也就是18*9=162，所以[s,s+1000]这个范围直接枚举，更大的肯定是满足的。

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
#include<map>
#include<vector>
#include<set>
#define il inline
#define re register
using namespace std;
typedef long long ll;
ll n,m,ans;
il ll f(ll n){
    ll res=;
    for(;n;n/=)
        res+=(n%);
    return res;
}
int main(){
    cin>>n>>m;
    for(ll i=m;i<=n&&i<=m+;i++){
        if(i-f(i)>=m) ans++;
    }
    ans+=n-min(n,m+);
    cout<<ans;
    return ;
}

D

给定一个长度为n的数组a (n<=100000)

求sigma(max(i,j)-min(i,j)) (1<=i<=j<=n)

【solution】

显然的把最大和最小拆开做

我们采用分治算法解决问题

我们去除一段中最大（小）统计贡献，然后左右递归

最多递归n次，采用st算法加速

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
#include<map>
#include<vector>
#include<set>
#define il inline
#define re register
#define cmin(x,y) (a[x]<a[y]?x:y)
#define cmax(x,y) (a[x]>a[y]?x:y)
using namespace std;
typedef long long ll;
const int N=;
int n,s[N][],t[N][],a[N],k[N];
ll ans=;
il int getmin(int l,int r){
    int h=r-l+,p=r-(<<k[h])+;
    return cmin(s[l][k[h]],s[p][k[h]]);
}
il int getmax(int l,int r){
    int h=r-l+,p=r-(<<k[h])+;
    return cmax(t[l][k[h]],t[p][k[h]]);
}
il void dfs1(int l,int r){
    if(l>r) return;
    int mid=getmin(l,r);
    ans-=(ll)a[mid]*(mid-l+)*(r-mid+);
    dfs1(l,mid-);dfs1(mid+,r);
}
il void dfs2(int l,int r){
    if(l>r) return;
    int mid=getmax(l,r);
    ans+=(ll)a[mid]*(mid-l+)*(r-mid+);
    dfs2(l,mid-);dfs2(mid+,r);
}
int main(){
    scanf("%d",&n);
    for(int i=,K=;i<=n;i++){
        if((<<K+)<i) K++;
        scanf("%d",&a[i]);k[i]=K;
        t[i][]=s[i][]=i;
    }
    for(int j=;j<=k[n];j++){
        for(int i=,k=(<<j-)+;k<=n;i++,k++){
            s[i][j]=cmin(s[i][j-],s[k][j-]);
            t[i][j]=cmax(t[i][j-],t[k][j-]);
        }
    }
    dfs1(,n);dfs2(,n);
    cout<<ans;
    return ;
}

E

维护一个正整数构成的集合p

支持三个操作

1、添加一个元素

2、删除一个已经存在的元素

3、输入x,y，询问集合中满足pi^x<y的元素有多少个。

【solution】

解法十分的巧妙，把元素转化成二进制，建立trie树，问题迎刃而解。

希望这种做法能在难题里得到应用。

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
#include<map>
#include<vector>
#include<set>
#define il inline
#define re register
using namespace std;
const int N=;
int n=,Q,c[N*10][],s[N*10];
int main(){
    scanf("%d",&Q);
    for(int ii=,jj,x,y,h,ans;ii<=Q;ii++){
        scanf("%d%d",&jj,&x);h=;
        if(jj==){
            for(int i=,j;i>=;i--){
                j=(x&(<<i))>;
                if(!c[h][j]) c[h][j]=(++n);
                h=c[h][j];s[h]++;
            }
        }
        if(jj==){
            for(int i=,j;i>=;i--){
                j=(x&(<<i))>;
                h=c[h][j];s[h]--;
            }
        }
        if(jj==){
            scanf("%d",&y);ans=;
            for(int i=;i>=;i--){
                if(y&(<<i)){
                    if(x&(<<i)){
                        ans+=s[c[h][]];
                        h=c[h][];
                    }
                    else{
                        ans+=s[c[h][]];
                        h=c[h][];
                    }
                }
                else{
                    if(x&(<<i)) h=c[h][];
                    else h=c[h][];
                }
            }
            printf("%d\n",ans);
        }
    }
    return ;
}

F

维护区间裸题

1、染黑一个区间

2、染白一个区间

3、翻转一个区间

操作后要求输出最靠左的黑点的坐标

【solution】

线段树

细节：有的标记不能简单覆盖！【以前一直忽略的！】

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
#include<map>
#include<vector>
#include<set>
#define il inline
#define re register
using namespace std;
typedef long long ll;
const int N=;
int t[N],Q,m=,L[N],R[N],s[N],p,c[N];
ll l[N],r[N],b[N];
il int d(int a,int b){
    if(a==) return b;
    if(b<) return b;
    return -a;
}
il void pushdown(int i){
    if(t[i]==) return;
    if(t[i]==){
        t[i+i]=t[i+i+]=;
        s[i+i]=R[i+i]-L[i+i]+;
        s[i+i+]=R[i+i+]-L[i+i+]+;
        t[i]=;
    }
    else if(t[i]==){
        t[i+i]=t[i+i+]=;
        s[i+i]=s[i+i+]=;
        t[i]=;
    }
    else if(t[i]==){
        t[i+i]=d(t[i+i],t[i]);
        t[i+i+]=d(t[i+i+],t[i]);
        s[i+i]=R[i+i]-L[i+i]+-s[i+i];
        s[i+i+]=R[i+i+]-L[i+i+]+-s[i+i+];
        t[i]=;
    }
}
il void work(int i,int p,int q,int v){
    if(q<L[i]||p>R[i]) return;
    if(i<m) pushdown(i);
    if(p<=L[i]&&R[i]<=q){
        if(v==) s[i]=R[i]-L[i]+;
        if(v==) s[i]=;
        if(v==) s[i]=R[i]-L[i]+-s[i];
        t[i]=d(t[i],v);
        return;
    }
    work(i+i,p,q,v);work(i+i+,p,q,v);
    s[i]=s[i+i]+s[i+i+];
}
il int query(int i){
    if(i<m) pushdown(i);
    if(s[i]==) return L[i];
    if(s[i+i]<R[i+i]-L[i+i]+) return query(i+i);
    else return query(i+i+);
}
int main(){
    scanf("%d",&Q);
    for(int i=;i<=Q;i++){
        scanf("%d%I64d%I64d",&c[i],&l[i],&r[i]);
        b[++p]=l[i];b[++p]=l[i]+;
        b[++p]=r[i];b[++p]=r[i]+;
    }
    b[++p]=;
    sort(b+,b+p+);
    p=unique(b+,b+p+)-b-;
    for(int i=;i<=Q;i++){
        l[i]=lower_bound(b+,b+p+,l[i])-b;
        r[i]=lower_bound(b+,b+p+,r[i])-b;
    }
    while(m<p) m<<=;
    for(int i=m;i<m+m;i++)
        L[i]=R[i]=i-m+;
    for(int i=m-;i;i--)
        L[i]=L[i+i],R[i]=R[i+i+];
    for(int i=;i<=Q;i++){
        work(,l[i],r[i],c[i]);
        printf("%I64d\n",b[query()]);
    }
    return ;
}