2019.3.12考试&2019.3.13考试&ESTR

过程：太菜了，不写了

T1 基环树直径，一定学

T2 树上斜率优化，类似购票，数据结构/分治算法，一定改

(把点按深度排序倒着跑2e7次斜率优化也能A，orz zyz)

T3 CC原题，码码码，一定补

一定咕

学动态点分治去了

因为各种原因又压进来一篇

过程：太菜了，不写了

T1 神tm 暴力DP+剪枝可过，我以为是暴力然后DP就没剪枝

T2 沙茶博主第一次实际应用生成函数？

根据题目中的递推关系搞出来生成函数

$f[i]=2*f[i-1]+3*f[i-2]$

$x^n=2*x^{n-1}+3*x^{n-2}$

$x^2=2x+3$

解这个方程得到$x=-1$或$x=3$

所以一定有$f_n=k_1(-1)^n+k_23^n$

前两项带进去，解得$k_1=\frac{3}{4}f_0-\frac{1}{4}f_1,k_2=\frac{1}{4}f_0+\frac{1}{4}f_1$

现在要我们求集合s的所有大小为k的子集的子集和的对应项之和

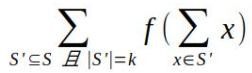
考虑上面的那个东西，相当于把所有物品拿出来做背包，最后$k$次项的系数对答案产生贡献，写一个分治FFT来做

 #include<cmath>
 #include<cstdio>
 #include<cctype>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int N=,M=,mod=;
 const int Pow=,Bas=(<<Pow)-;
 const double pai=acos(-);
 struct cpx
 {
     double x,y;
     void Turn(int a,int b)
     {
         x=a,y=b;
     }
 }a[N],b[N],c[N],d[N],ort[N];
 const cpx b1=(cpx){0.5,};
 const cpx b2=(cpx){,-0.5};
 const cpx b3=(cpx){,};
 const cpx b4=(cpx){,};
 cpx operator + (cpx a,cpx b)
 {
     return (cpx){a.x+b.x,a.y+b.y};
 }
 cpx operator - (cpx a,cpx b)
 {
     return (cpx){a.x-b.x,a.y-b.y};
 }
 cpx operator * (cpx a,cpx b)
 {
     double x1=a.x,x2=b.x,y1=a.y,y2=b.y;
     return (cpx){x1*x2-y1*y2,x1*y2+x2*y1};
 }
 cpx operator ! (cpx a)
 {
     a.y=-a.y; return a;
 }
 char BF[<<],*P1=BF,*P2=BF;
 char Gc(){return (P1==P2&&(P2=(P1=BF)+fread(BF,,<<,stdin),P1==P2)?EOF:*P1++);}
 template<class Type> void Fread(Type &x)
 {
     x=; char ch=Gc();
     while(!isdigit(ch)) ch=Gc();
     while(isdigit(ch)) x=(x<<)+(x<<)+(ch^),ch=Gc();
 }
 int Roumod(double x)
 {
     return (long long)(x+0.5)%mod;
 }
 int Qpow(int x,int k)
 {
     if(k==) return x;
     int tmp=Qpow(x,k/);
     return k%?1ll*tmp*tmp%mod*x%mod:1ll*tmp*tmp%mod;
 }
 #define vint vector<int>
 #define vit vector<int> ::iterator
 double Sin[M],Cos[M];
 int n,m,f0,f1,k1,k2,anss;
 int num[N],odf[N],rev[N],xx[N],yy[N],ans[N]; vint fuc;

 void Trans(cpx *cop,int len,int typ)
 {
     register int i,j,k;
     for(i=;i<len;i++)
         if(rev[i]>i) swap(cop[i],cop[rev[i]]);
     for(i=;i<=len;i<<=)
     {
         int lth=i>>;
         for(j=;j<len;j+=i)
         {
             cpx *pts=ort;
             for(k=j;k<j+lth;pts+=len/lth,k++)
             {
                 cpx tmp=*pts; if(typ==-) tmp=!tmp;
                 tmp=tmp*cop[k+lth],cop[k+lth]=cop[k]-tmp,cop[k]=cop[k]+tmp;
             }
         }
     }
     if(typ==-)
         for(int i=;i<=len;i++)
             cop[i].x/=len,cop[i].y/=len;
 }
 void Mul(cpx *c1,cpx *c2,cpx &a1,cpx &a2,int p,int q)
 {
     cpx t1=(c1[p]+!c1[q])*b1,t2=(c1[p]-!c1[q])*b2;
     cpx t3=(c2[p]+!c2[q])*b1,t4=(c2[p]-!c2[q])*b2;
     a1=t1*t3+(t1*t4+t2*t3)*b4,a2=t2*t4;
 }
 void CDFFT(int *p1,int *p2,int *ans,int len)
 {
     register int i;
     for(i=;i<len;i++)
     {
         a[i].Turn(p1[i]&Bas,p1[i]>>Pow),p1[i]=;
         b[i].Turn(p2[i]&Bas,p2[i]>>Pow),p2[i]=;
     }
     Trans(a,len,),Trans(b,len,),Mul(a,b,c[],d[],,);
     for(i=;i<len;i++) Mul(a,b,c[i],d[i],i,len-i);
     Trans(c,len,-),Trans(d,len,-);
     for(i=;i<len;i++)
     {
         long long x1=Roumod(c[i].x),y1=Roumod(c[i].y),x2=Roumod(d[i].x);
         ans[i]=(((x2<<(Pow<<))+(y1<<Pow)+x1)%mod+mod)%mod;
     }
 }
 vint Merge(vint v1,vint v2)
 {
     register int i;
     vint ret; ret.clear();
     int l1=v1.size()-,l2=v2.size()-,len=l1+l2;
     for(i=;i<=l1;i++) xx[i]=v1[i];
     for(i=;i<=l2;i++) yy[i]=v2[i];
     int lth=; while(lth<=len) lth<<=;
     for(i=;i<=lth;i++)
     {
         rev[i]=(rev[i>>]>>)+(i&)*(lth>>);
         ort[i]=(cpx){cos(pai*i/lth),sin(pai*i/lth)};
     }
     CDFFT(xx,yy,ans,lth);
     for(i=;i<=len;i++) ret.push_back(ans[i]);
     return ret;
 }
 vint CDQ(int l,int r)
 {
     if(l==r)
     {
         vint ret; ret.clear();
         ret.push_back();
         ret.push_back(odf[l]);
         return ret;
     }
     else
     {
         int mid=(l+r)>>;
         vint ls=CDQ(l,mid);
         vint rs=CDQ(mid+,r);
         return Merge(ls,rs);
     }
 }
 int main()
 {
     register int i;
     Fread(n),Fread(m);
     for(i=;i<=n;i++) Fread(num[i]);
     Fread(f0),Fread(f1);
     k2=1ll*(f0+f1)*Qpow(,mod-)%mod,k1=(f0-k2+mod)%mod;
     for(i=;i<=n;i++) odf[i]=num[i]%?(mod-):;
     fuc=CDQ(,n),anss=1ll*fuc[m]*k1%mod;
     for(i=;i<=n;i++) odf[i]=Qpow(,num[i]);
     fuc=CDQ(,n),anss=(anss+1ll*fuc[m]*k2%mod)%mod;
     printf("%d",anss);
     return ;
 }

T3

因为各种原因 ESTR 也被扔进来了

T1 取最长的相同的一段即为答案，证明脑补

T2 循环矩阵的矩阵乘法

不动的矩阵先自己快速幂，然后两个对应乘起来即可，多项式乘法优化到$O(n\log^2 n)$，因为用的是vector所以常数惨不忍睹=。=

 #pragma GCC optimize(2)
 #include<cmath>
 #include<cstdio>
 #include<cctype>
 #include<vector>
 #include<cstring>
 #include<algorithm>
 #define vint vector<int>
 #define vit vector<int> ::iterator
 using namespace std;
 const int N=,mod=;
 int n,m,rd,lim,len,G,Gi,Ni; long long t;
 int a[N],b[N],c[N],rev[N],pw[][]; vint aa,bb;
 void Add(int &x,int y){x+=y;if(x>=mod) x-=mod;}
 int Qpow(int x,int k)
 {
     if(k==) return x;
     int tmp=Qpow(x,k/);
     return k%?1ll*tmp*tmp%mod*x%mod:1ll*tmp*tmp%mod;
 }

 void Pre()
 {
     register int i;
     G=,Gi=Qpow(G,mod-);
     lim=*n-,len=; while(len<=lim) len<<=;
     for(int i=;i<=len;i++)
         rev[i]=(rev[i>>]>>)+(i&)*(len>>);
     for(int i=;i<=;i++)
     {
         pw[i][]=Qpow(G,(mod-)/(<<i));
         pw[i][]=Qpow(Gi,(mod-)/(<<i));
     }
 }
 void Trans(int *arr,int len,int typ)
 {
     register int i,j,k;
     for(i=;i<len;i++)
         if(rev[i]>i) swap(arr[rev[i]],arr[i]);
     for(i=;i<=len;i<<=)
     {
         int lth=i>>,ort=pw[(int)log2(i)][typ==-];
         for(j=;j<len;j+=i)
         {
             int ori=,tmp;
             for(k=j;k<j+lth;k++,ori=1ll*ori*ort%mod)
             {
                 tmp=1ll*ori*arr[k+lth]%mod;
                 arr[k+lth]=(arr[k]-tmp+mod)%mod;
                 arr[k]=(arr[k]+tmp)%mod;
             }
         }
     }
     if(typ==-)
     {
         int Ni=Qpow(len,mod-);
         for(i=;i<=len;i++)
             arr[i]=1ll*arr[i]*Ni%mod;
     }
 }
 vint Pmul(vint va,vint vb)
 {
     vint ret; ret.clear();
     for(int i=;i<n;i++) a[i]=va[i],b[i]=vb[i];
     for(int i=n;i<=len;i++) a[i]=b[i]=;
     Trans(a,len,),Trans(b,len,);
     for(int i=;i<=len;i++) a[i]=1ll*a[i]*b[i]%mod;
     Trans(a,len,-); ret.resize(n);
     for(int i=;i<*n-;i++) Add(ret[i%n],a[i]);
     return ret;
 }
 vint Ppow(vint x,long long k)
 {
     if(k==) return x;
     vint tmp=Ppow(x,k>>);
     return k%?Pmul(Pmul(tmp,tmp),x):Pmul(tmp,tmp);
 }
 int main()
 {
     scanf("%d%lld",&n,&t),Pre();
     for(int i=;i<n;i++) scanf("%d",&rd),aa.push_back(rd);
     for(int i=;i<n;i++) scanf("%d",&rd),bb.push_back(rd);
     bb=Ppow(bb,t),reverse(bb.begin(),bb.end()),aa=Pmul(aa,bb);
     printf("%d ",aa[n-]); for(int i=;i<n-;i++) printf("%d ",aa[i]);
     return ;
 }

T3

若[l,r]中有两个x的倍数，那么一定存在一个a使得a*x和(a+1)*x在[l,r]中，数论分块可过。

可以发现这是有一个分界线的，分界线之后都不合法，也许找出分界线也可以做？

上面fpn，显然假的

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 long long l,r,k;
 int main()
 {
     scanf("%lld%lld%lld",&l,&r,&k);
     if(k==) printf("%lld",r-l+),exit();
     long long ll=l-,res=;
     for(long long i=,j;i<=ll;i=j+)
     {
         j=min(ll/(ll/i),r/(r/i));
         if(r/i-ll/i>=) res+=j-i+;
     }
     printf("%lld",r-l++res);
     return ;
 }