Vigenere加密

Vigenere加密法原理很简单，实现起来也不难。与普通的单码加密法不同，明文经过加密之后，每个字母出现的频率就不会有高峰和低峰。

密钥中字母代表行和明文中的字母代表行。在vigenere表中找到对应的字母即可。当明文的长度大于密钥的长度的时候，密钥重复使用。下面是go语言的实现版本。

　　　　　　　　　　　　vigenege表

var arr [][]int //Vigenere表
var key string = "hold" //密钥
//初始化vigenere表
func init() {
    arr[][] =
    for i := ; i < ; i++ {
        for j := ; j < ; j++ {
            arr[i][j] = 'a' + j -
        }
    }
    for i := ; i < ; i++ {
        arr[i][] = 'a' + i -
    }
    var num int =
    for i := ; i > ; i-- {
        for j := ; j < ; j++ {
            arr[j][i] = 'a' + num
            num++
            if num% ==  {
                num =
            }
        }
    }
}
//进行加密
func encrypt(str string) []byte {
    count :=
    var ciphertext []byte = []byte(str)
    length := len(key)
    for i := ; i < len(str); i++ {
        ciphertext[i] = byte(arr[str[i]-'a'+][key[count]-'a'+])
        count++
        count %= length
    }
    return ciphertext
}

在很长的一段时间内Vigenere加密法一直被认为是无法破解的。我们可以通过IC(index of coincidence)值来得到密钥的长度。这里还要用到MR(measure of roughness)。当所有字母都均匀分布，那么选取每个字母的概率都相同。为1/26。那么从一段密文中选取某个字母的概率与均匀分布的概率偏差为

　　　　　　　　　　　　　　　　　　　　　　　　　　　

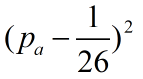
MR就是a-z中所有的字母的偏差的和。

　　　　　　　　　　　　　　　　　　　　　　　　 

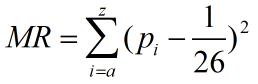
展开后在进行一些简单的计算可以得到

　　　　　　　　　　　　　　　　　　　　　　　　

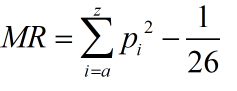
在MR中唯一依赖密文的地方就是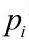。其值为密文中 i 单词出现的次数与密文长度的比值。那么和IC为

　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　

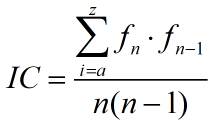
知道了IC值之后，我们可以用IC值，当IC值在0.038与0.066之间时。则表示采用了多码加密法。但我们任然无法准确的得到密钥的长度。1863年Kasiski提出了破解Vigenere的方法。当我们利用密钥加密的时候，总是重复的利用密钥进行加密，当加密后的密文中有重复的字符串则是密钥中相同的部分加密后得到的。当然，也有可能是偶然情况导致的，不过偶然情况不可能出现长串的相同字符串。因此偶然情况的影响可以消除。如下,第一段的 RUN 为密钥，中间是明文，最后为加密后的密文。

R U N R U N R U N R U N R U N R U N R U N R U N R U N
t o b e o r n o r t o b e t h a t i s t h e q u e s t
K L O V I E E I G K I O V N U R N V J N U V K H V M G

可以观察到密文中'KLOV'出现了两次，‘NU’同样也出现了两次。而重复出现的密文则表示了密钥使用的次数。因此，上述的密钥长度应为6和9的公约数。当获得足够多的密文之后，就可以得到密钥的长度。

有了密钥的长度就意味着我们可以把密文分为密钥长度个集合，且这些集合是由同个字母单码加密得到的。比如上述密文，我们得到密钥长度为3，对于密文，我们每3个一循环，那么我们可以得到3个集合

K V E K V R J V V    由R加密的集合
L I I I N N N K M    由U加密的集合
O E G O U V U H G    由N加密的集合

接下来我们可以分别破解3个由单码加密的密文，Vigenere则宣告被破解。