回归算法比较（线性回归，Ridge回归，Lasso回归）

代码实现：

 # -*- coding: utf-8 -*-
 """
 Created on Mon Jul 16 09:08:09 2018

 @author: zhen
 """

 from sklearn.linear_model import LinearRegression, Ridge, Lasso
 import mglearn
 from sklearn.model_selection import train_test_split
 import matplotlib.pyplot as plt
 import numpy as np
 # 线性回归
 x, y = mglearn.datasets.load_extended_boston()
 x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0)

 linear_reg = LinearRegression()
 lr = linear_reg.fit(x_train, y_train)

 print("lr.coef_:{}".format(lr.coef_))  # 斜率
 print("lr.intercept_:{}".format(lr.intercept_))  # 截距

 print("="*25+"线性回归"+"="*25)
 print("Training set score:{:.2f}".format(lr.score(x_train, y_train)))
 print("Rest set score:{:.2f}".format(lr.score(x_test, y_test)))

 """
     总结：
         训练集和测试集上的分数非常接近，这说明可能存在欠耦合。
         训练集和测试集之间的显著性能差异是过拟合的明显标志。解决方式是使用岭回归！
 """
 print("="*25+"岭回归（默认值1.0）"+"="*25)
 # 岭回归
 ridge = Ridge().fit(x_train, y_train)

 print("Training set score:{:.2f}".format(ridge.score(x_train, y_train)))
 print("Test set score:{:.2f}".format(ridge.score(x_test, y_test)))

 print("="*25+"岭回归（alpha=10）"+"="*25)
 # 岭回归
 ridge_10 = Ridge(alpha=10).fit(x_train, y_train)

 print("Training set score:{:.2f}".format(ridge_10.score(x_train, y_train)))
 print("Test set score:{:.2f}".format(ridge_10.score(x_test, y_test)))

 print("="*25+"岭回归（alpha=0.1）"+"="*25)
 # 岭回归
 ridge_01 = Ridge(alpha=0.1).fit(x_train, y_train)

 print("Training set score:{:.2f}".format(ridge_01.score(x_train, y_train)))
 print("Test set score:{:.2f}".format(ridge_01.score(x_test, y_test)))

 # 可视化
 fig = plt.figure(10)
 plt.subplots_adjust(wspace =0, hspace =0.6)#调整子图间距
 ax1 = plt.subplot(2, 1, 1)

 ax2 = plt.subplot(2, 1, 2)

 ax1.plot(ridge_01.coef_, 'v', label="Ridge alpha=0.1")
 ax1.plot(ridge.coef_, 's', label="Ridge alpha=1")
 ax1.plot(ridge_10.coef_, '^', label="Ridge alpha=10")

 ax1.plot(lr.coef_, 'o', label="LinearRegression")

 ax1.set_ylabel("Cofficient magnitude")
 ax1.set_ylim(-25,25)
 ax1.hlines(0, 0, len(lr.coef_))
 ax1.legend(ncol=2, loc=(0.1, 1.05))

 print("="*25+"Lasso回归（默认配置）"+"="*25)
 lasso = Lasso().fit(x_train, y_train)

 print("Training set score:{:.2f}".format(lasso.score(x_train, y_train)))
 print("Test set score:{:.2f}".format(lasso.score(x_test, y_test)))
 print("Number of features used:{}".format(np.sum(lasso.coef_ != 0)))

 print("="*25+"Lasso回归（aplpha=0.01）"+"="*25)
 lasso_001 = Lasso(alpha=0.01, max_iter=1000).fit(x_train, y_train)

 print("Training set score:{:.2f}".format(lasso_001.score(x_train, y_train)))
 print("Test set score:{:.2f}".format(lasso_001.score(x_test, y_test)))
 print("Number of features used:{}".format(np.sum(lasso_001.coef_ != 0)))

 print("="*15+"Lasso回归（aplpha=0.0001）太小可能会过拟合"+"="*15)
 lasso_00001 = Lasso(alpha=0.0001, max_iter=1000).fit(x_train, y_train)

 print("Training set score:{:.2f}".format(lasso_00001.score(x_train, y_train)))
 print("Test set score:{:.2f}".format(lasso_00001.score(x_test, y_test)))
 print("Number of features used:{}".format(np.sum(lasso_00001.coef_ != 0)))

 # 可视化
 ax2.plot(ridge_01.coef_, 'o', label="Ridge alpha=0.1")
 ax2.plot(lasso.coef_, 's', label="lasso alpha=1")
 ax2.plot(lasso_001.coef_, '^', label="lasso alpha=0.001")
 ax2.plot(lasso_00001.coef_, 'v', label="lasso alpha=0.00001")

 ax2.set_ylabel("Cofficient magnitude")
 ax2.set_xlabel("Coefficient index")
 ax2.set_ylim(-25,25)
 ax2.legend(ncol=2, loc=(0.1, 1))

结果：

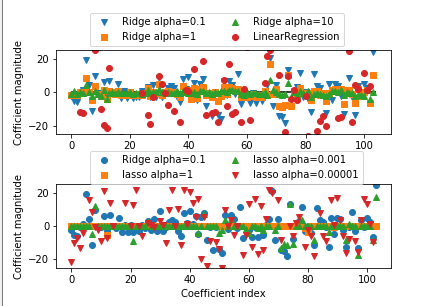
总结：各回归算法在相同的测试数据中表现差距很多，且算法内的配置参数调整对自身算法的效果影响也是巨大的，

　　因此合理挑选合适的算法和配置合适的配置参数是使用算法的关键！