排序算法入门之堆排序（Java实现）

堆排序

在学习了二叉堆（优先队列）以后，我们来看看堆排序。堆排序总的运行时间为O(NlonN)。

堆的概念

堆是以数组作为存储结构。

可以看出，它们满足以下规律：

设当前元素在数组中以R[i]表示，那么（下标从0开始），

(1) 它的左孩子结点是：R[2*i+1];

(2) 它的右孩子结点是：R[2*i+2];

(3) 它的父结点是：R[(i-1)/2];

(4) R[i] <= R[2*i+1] 且 R[i] <= R[2i+2]。

(5)最后一个父节点是N/2-1;(构建堆要从这里开始下滤)

要点

首先，按堆的定义将数组R[0..n]调整为大根堆（这个过程称为创建初始堆），交换R[0]和R[n]，这样最大值去了数组的最后一个；

然后，将R[0..n-1]调整为堆，交换R[0]和R[n-1]；

如此反复，直到交换了R[0]和R[1]为止。

以上思想可归纳为两个操作：

（1）根据初始数组去构造初始堆（构建一个完全二叉树，保证所有的父结点都比它的孩子结点数值大）。

（2）每次交换第一个和最后一个元素，输出最后一个元素（将它放到数组最后）（最大值），然后把剩下元素重新调整为大根堆。

当输出完最后一个元素后，这个数组已经是按照从小到大的顺序排列了。

先通过详细的实例图来看一下，如何构建初始堆。

构建初始堆，从最后一个父节点开始往数组前面遍历，遍历所有父节点，将这些父节点对应的子树构成局部大根堆，将孩子中较大的节点放到父节点处，父节点下滤到孩子处，然后继续和下面的孩子比较，继续下滤。

设有一个无序序列 { 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 }。

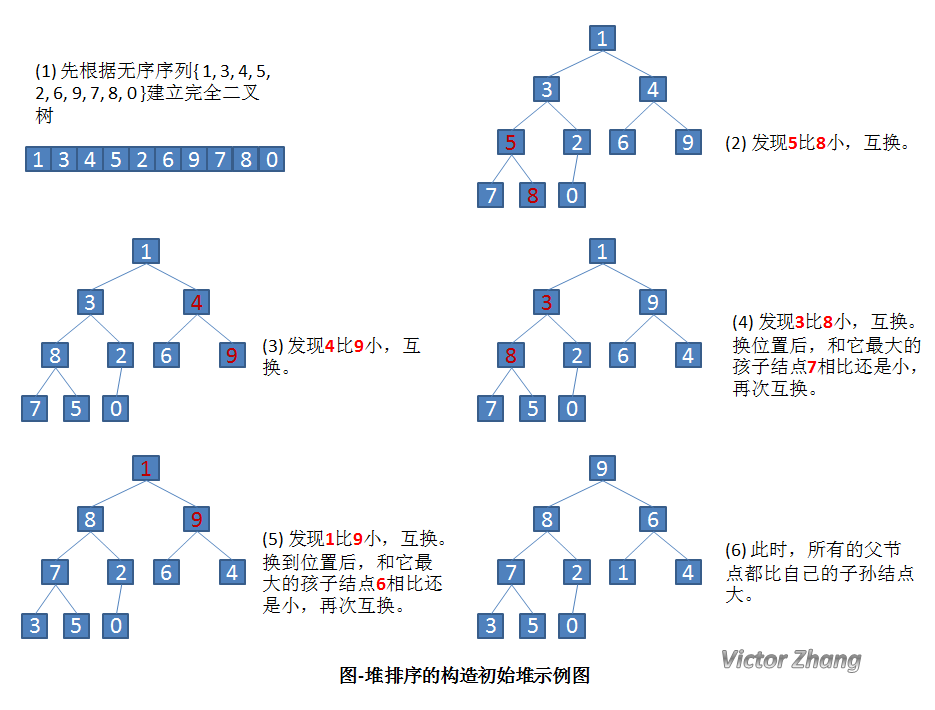
构造了初始堆后，我们来看一下完整的堆排序处理：

还是针对前面提到的无序序列 { 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 } 来加以说明。

相信，通过以上两幅图，应该能很直观的演示堆排序的操作处理。

构建大（小）根堆的下滤：选择孩子节点中较大（小）的节点取代父节点。。

核心代码...(数组从0开始填数据)

 //构建的是大根堆
public void HeapAdjust(int[] array, int parent, int length) {
    int temp = array[parent]; // temp保存当前父节点
    int child = 2 * parent + 1; // 先获得左孩子
 
    while (child < length) {
        // 如果有右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点
        if (child != length-1 && array[child] < array[child + 1]) {
            child++;
        }
 
        // 如果父结点的值已经大于孩子结点的值，则直接结束
        if (temp >= array[child])
            break;
 
        // 父节点小于孩子节点，把孩子结点的值赋给父结点
        array[parent] = array[child];
 
        // 选取孩子结点的左孩子结点,继续向下筛选
        parent = child;
        child = 2 * child + 1;
    }
 
    array[parent] = temp;
}
 
public void heapSort(int[] list) {
    // 从最后一个父节点开始循环建立初始堆
　　　　/*
　　构建堆的时候，从最后一个父节点开始，每个父节点和自己的左右子树比较，将自己这一子树（从自己到叶子）构建成大根堆。每个父节点下滤时，不用考虑他的父节点和兄弟节点，只需考虑孩子即可。
*/
    for (int i = list.length / 2-1; i >= 0; i--) {
        HeapAdjust(list, i, list.length);
    }
 
    // 进行n-1次循环，完成排序
    for (int i = list.length - 1; i > 0; i--) {
        // 最后一个元素和第一元素进行交换
        int temp = list[i];
        list[i] = list[0];
        list[0] = temp;
 
        // 筛选 R[0] 结点，得到i-1个结点的堆
        HeapAdjust(list, 0, i);
        
    }
}
 

算法分析

堆排序算法的总体情况

排序类别	排序方法	时间复杂度			空间复杂度	稳定性	复杂性
		平均情况	最坏情况	最好情况
选择排序	堆排序	O(nlog2n)	O(nlog2n)	O(nlog2n)	O(1)	不稳定	较复杂

时间复杂度

堆的存储表示是顺序的。因为堆所对应的二叉树为完全二叉树，而完全二叉树通常采用顺序存储方式。

当想得到一个序列中第k个最小的元素之前的部分排序序列，最好采用堆排序。

因为堆排序的时间复杂度是O(n+klog2n)，若k≤n/log2n，则可得到的时间复杂度为O(n)。

算法稳定性

堆排序是一种不稳定的排序方法。

因为在堆的调整过程中，关键字进行比较和交换所走的是该结点到叶子结点的一条路径，

因此对于相同的关键字就可能出现排在后面的关键字被交换到前面来的情况。

转载：https://www.cnblogs.com/jingmoxukong/p/4303826.html