浮点型 float和double类型的内存结构和精度问题

首先引用一个例子在java中可能你会遇到这样的问题：

例：0.99999999f==1f //true

　　0.9999999f==1f //false

这是超出精度造成的，为了知道为什么会造成这样的问题，首先了解一下float和double的内存结构

1.内存结构

float和double的范围是由指数的位数来决定的。
float的指数位有8位，而double的指数位有11位，分布如下：

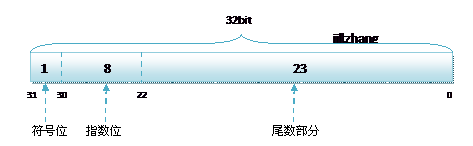
float：1bit（符号位） 8bits（指数位） 23bits（尾数位）

double：1bit（符号位） 11bits（指数位） 52bits（尾数位）

float的指数范围为-128~+127，而double的指数范围为-1024~+1023，并且指数位是按补码的形式来划分的。

float的范围为-2^128 ~ +2^127，也即-3.40E+38 ~ +3.40E+38；double的范围为-2^1024 ~ +2^1023，也即-1.79E+308 ~ +1.79E+308。

Float.MAX_VALUE = 3.4028235E38

Float.MIN_VALUE = 1.4E-45

Double.MAX_VALUE = 1.7976931348623157E308

Double.MIN_VALUE = 4.9E-324

public class DoubleBinaryTest {
    public static void main(String[] args) {
        /*
         * float类型的二进制存储是4个字节32位
         * 1位符号位   8位阶码位  23位尾数位
         * 1、将十进制40.125转换为整数部分和小数部分的二进制  101000.001
         * 2、转换为 1.01000001 * 2的5次方
         * 3、符号位为0
         * 4、指数e=阶码E-127，阶码位，5=E-127,E=132,转换为二进制为10000100
         * 5、小数位，0100000100000000000000
         * 6、40.125f的二进制表现形式为01000010 00100000 10000000 00000000
         */
        float f = 40.125f;
        int i = Float.floatToIntBits(f);//Float类的静态方法，以int类型的方式返回这个小数的二进制形式
        System.out.println(Integer.toBinaryString(i));

        /*
         * double类型的二进制存储是8个字节64位
         * 1位符号位 ，11位的阶码，52位的尾数位
         * 和float同理，只是阶码位不一样
         * E-1023=5,E=1028,转换为10000000100
         * 40.125d的二进制为 01000000 01000100 00010000 00000000 00000000 00000000 00000000 00000000
         */
        double d = 40.125;
        long l = Double.doubleToLongBits(d);
        System.out.println(Long.toBinaryString(l));

        /*
         * float类型的二进制存储是4个字节32位
         * 1位符号位   8位阶码位  23位尾数位
         * 1、将十进制-40.125转换为整数部分和小数部分的二进制  -101000.001
         * 2、转换为 -1.01000001 * 2的5次方
         * 3、符号位为1
         * 4、阶码位，E-127=5,E=132,转换为二进制为10000100
         * 5、小数位，0100000100000000000000
         * 6、40.125f的二进制表现形式为11000010 00100000 10000000 00000000
         */
        float f2 = -40.125f;
        int i2 = Float.floatToIntBits(f2);
        System.out.println(Integer.toBinaryString(i2));
    }
}

清楚了浮点型型的存储方式后，再来看例题在计算机中怎么存储的

（1）0.99999999f 化为二进制表示：0011 1111 1000 0000 0000 0000 0000 0000

（2）0.9999999f 化为二进制表示：0011 1111 0111 1111 1111 1111 1111 1110

（3）1f 化为二进制表示：0011 1111 1000 0000 0000 0000 0000 0000

通过计算后发现（2）和（3）我们可以根据上述方式计算出来二进制表示方式，但是（1）话就和我们算出来的不一样了，为什么会这样呢，接下来我们再了解一下浮点型的精度。

2.关于精度：

float和double的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的，其整数部分始终是一个隐含着的“1”，由于它是不变的，故不能对精度造成影响。

float：2^23 = 8388608，一共七位，由于最左为1的一位省略了，这意味着最多能表示8位数： 2*8388608 = 16777216 。有8位有效数字，但绝对能保证的为7位，也即float的精度为7~8位有效数字；
double：2^52 = 4503599627370496，一共16位，同理，double的精度为16~17位。

我们可以用下面这段代码检验一下：

1. float f1 = 16777215f;
2. for (int i = 0; i < 10; i++) {
3. System.out.println(f1);
4. f1++;
5. }

对于小数来说，更容易会因为精度而出错误。

1. float f = 2.2f;
2. double d = (double) f;
3. System.out.println(d);
4. f = 2.25f;
5. d = (double) f;
6. System.out.println(d);

输出结果为：

2.200000047683716
        2.25

对于这种简单数的输出结果会是这样，是简直无法忍受的。

其实通过上面关于两种存储结果的介绍，我们已经大概能找到答案。首先我们看看2.25的单精度存储方式，转化为2进制位便是10.01，整理为1.001*2 很简单

于是我们可以写出2.25的内存分布： 
        符号位为：0
        指数为1，用补码表示 0000 0001，转为移码就是1000 0001。
        尾数位为0010 0000 0000 0000 0000 000

而2.25的双精度表示为:0 100 0000 0001 0010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,这样2.25在进行强制转换的时候，数值是不会变的，而我们再看看2.2呢，2.2用科学计数法表示应该为：将十进制的小数转换为二进制的小数的方法为将小数*2，取整数部分，所以0.282=0.4，所以二进制小数第一位为0.4的整数部分0，0.4×2=0.8，第二位为0,0.8*2=1.6,第三位为1，0.6×2 = 1.2，第四位为1，0.2*2=0.4，第五位为0，这样永远也不可能乘到=1.0，得到的二进制是一个无限循环的排列 00110011001100110011... ,对于单精度数据来说，尾数只能表示24bit的精度，所以2.2的float存储为:

但是这样存储方式，换算成十进制的值，却不会是2.2的，因为十进制在转换为二进制的时候可能会不准确，如2.2，而double类型的数据也存在同样的问题，所以在浮点数表示中会产生些许的误差，在单精度转换为双精度的时候，也会存在误差的问题，如下面的代码，输出结果就不一样：

1. float f = 2.2f;
2. double d = (double) f;
3. System.out.println(f);
4. System.out.println(d);

对于能够用二进制表示的十进制数据，如2.25，这个误差就会不存在，所以会出现上面比较奇怪的输出结果。

3.关于BigDecimal

再如0.1f，java里面32位的float对0.1在内存当中的表示是不精确的，原理同上，

这个误差对我们生活小打小闹没啥影响，但是对科学计算和银行这样的应用或者领域是致命的，因此要用于银行以及科学计算会用java.math.BigDecimal提高精度，否则后果极其严重。

JAVA的浮点型是会丢失精度的，所以要用精确计算就用BigDecimal。

首先我们先来看如下代码示例：

1 public class Test_1 {
2     public static void main(String[] args) {
3         System.out.println(0.06+0.01);
4         System.out.println(1.0-0.42);
5         System.out.println(4.015*100);
6         System.out.println(303.1/1000);
7     }
8
9 }

运行结果如下。

0.06999999999999999

0.5800000000000001

401.49999999999994

0.30310000000000004

你认为你看错了，但结果却是是这样的。问题在哪里呢？原因在于我们的计算机是二进制的。浮点数没有办法是用二进制进行精确表示。我们的CPU表示浮点数由两个部分组成：指数和尾数，这样的表示方法一般都会失去一定的精确度，有些浮点数运算也会产生一定的误差。如：2.4的二进制表示并非就是精确的2.4。反而最为接近的二进制表示是 2.3999999999999999。浮点数的值实际上是由一个特定的数学公式计算得到的。

其实java的float只能用来进行科学计算或工程计算，在大多数的商业计算中，一般采用java.math.BigDecimal类来进行精确计算。

在使用BigDecimal类来进行计算的时候，主要分为以下步骤：

1、用float或者double变量构建BigDecimal对象。

2、通过调用BigDecimal的加，减，乘，除等相应的方法进行算术运算。

3、把BigDecimal对象转换成float，double，int等类型。

一般来说，可以使用BigDecimal的构造方法或者静态方法的valueOf()方法把基本类型的变量构建成BigDecimal对象。

1 BigDecimal b1 = new BigDecimal(Double.toString(0.48));
2 BigDecimal b2 = BigDecimal.valueOf(0.48);

对于常用的加，减，乘，除，BigDecimal类提供了相应的成员方法。

1 public BigDecimal add(BigDecimal value);                        //加法
2 public BigDecimal subtract(BigDecimal value);                   //减法
3 public BigDecimal multiply(BigDecimal value);                   //乘法
4 public BigDecimal divide(BigDecimal value);                     //除法

进行相应的计算后，我们可能需要将BigDecimal对象转换成相应的基本数据类型的变量，可以使用floatValue()，doubleValue()等方法。

下面是一个工具类，该工具类提供加，减，乘，除运算。

 1 public class Arith {
 2     /**
 3      * 提供精确加法计算的add方法
 4      * @param value1 被加数
 5      * @param value2 加数
 6      * @return 两个参数的和
 7      */
 8     public static double add(double value1,double value2){
 9         BigDecimal b1 = new BigDecimal(Double.valueOf(value1));
10         BigDecimal b2 = new BigDecimal(Double.valueOf(value2));
11         return b1.add(b2).doubleValue();
12     }
13
14     /**
15      * 提供精确减法运算的sub方法
16      * @param value1 被减数
17      * @param value2 减数
18      * @return 两个参数的差
19      */
20     public static double sub(double value1,double value2){
21         BigDecimal b1 = new BigDecimal(Double.valueOf(value1));
22         BigDecimal b2 = new BigDecimal(Double.valueOf(value2));
23         return b1.subtract(b2).doubleValue();
24     }
25
26     /**
27      * 提供精确乘法运算的mul方法
28      * @param value1 被乘数
29      * @param value2 乘数
30      * @return 两个参数的积
31      */
32     public static double mul(double value1,double value2){
33         BigDecimal b1 = new BigDecimal(Double.valueOf(value1));
34         BigDecimal b2 = new BigDecimal(Double.valueOf(value2));
35         return b1.multiply(b2).doubleValue();
36     }
37
38     /**
39      * 提供精确的除法运算方法div
40      * @param value1 被除数
41      * @param value2 除数
42      * @param scale 精确范围
43      * @return 两个参数的商
44      * @throws IllegalAccessException
45      */
46     public static double div(double value1,double value2,int scale) throws IllegalAccessException{
47         //如果精确范围小于0，抛出异常信息
48         if(scale<0){
49             throw new IllegalAccessException("精确度不能小于0");
50         }
51         BigDecimal b1 = new BigDecimal(Double.valueOf(value1));
52         BigDecimal b2 = new BigDecimal(Double.valueOf(value2));
53         return b1.divide(b2, scale).doubleValue();
54     }
55 }

另外需要注意的一点是：double小数转bigdecimal后四舍五入计算有误差

案例：

double g= 12.35;

BigDecimal bigG=new BigDecimal(g).setScale(1, BigDecimal.ROUND_HALF_UP); //期望得到12.4

System.out.println("test G:"+bigG.doubleValue());

test G:12.3

原因：

定义double g= 12.35;  而在计算机中二进制表示可能这是样：定义了一个g=12.34444444444444449，
new BigDecimal(g)   g还是12.34444444444444449 
new BigDecimal(g).setScale(1, BigDecimal.ROUND_HALF_UP); 得到12.3
正确的定义方式是使用字符串构造函数：
new BigDecimal("12.35").setScale(1, BigDecimal.ROUND_HALF_UP)

BigDecimal.setScale()方法用于格式化小数点
setScale(1)表示保留一位小数，默认用四舍五入方式 
setScale(1,BigDecimal.ROUND_DOWN)直接删除多余的小数位，如2.35会变成2.3 
setScale(1,BigDecimal.ROUND_UP)进位处理，2.35变成2.4 
setScale(1,BigDecimal.ROUND_HALF_UP)四舍五入，2.35变成2.4

setScaler(1,BigDecimal.ROUND_HALF_DOWN)四舍五入，2.35变成2.3，如果是5则向下舍

参考：

http://blog.csdn.net/zq602316498/article/details/41148063

http://bbs.csdn.net/topics/370105966

Java浮点数float和double精确计算的精度误差问题总结

Java精确运算（BigDecimal）

转：十进制小数转化为二进制小数