LSH(Locality Sensitive Hashing)原理与实现

原文地址：https://blog.csdn.net/guoziqing506/article/details/53019049

LSH(Locality Sensitive Hashing)翻译成中文，叫做“局部敏感哈希”，它是一种针对海量高维数据的快速最近邻查找算法。

在信息检索，数据挖掘以及推荐系统等应用中，我们经常会遇到的一个问题就是面临着海量的高维数据，查找最近邻。如果使用线性查找，那么对于低维数据效率尚可，而对于高维数据，就显得非常耗时了。为了解决这样的问题，人们设计了一种特殊的hash函数，使得2个相似度很高的数据以较高的概率映射成同一个hash值，而令2个相似度很低的数据以极低的概率映射成同一个hash值。我们把这样的函数，叫做LSH（局部敏感哈希）。LSH最根本的作用，就是能高效处理海量高维数据的最近邻问题

定义

我们将这样的一族hash函数 H={h:S→U}H={h:S→U} 称为是(r1,r2,p1,p2)(r1,r2,p1,p2) 敏感的，如果对于任意HH 中的函数hh ，满足以下2个条件：

1. 如果d(O1,O2)<r1d(O1,O2)<r1 ，那么Pr[h(O1)=h(O2)]≥p1Pr[h(O1)=h(O2)]≥p1
2. 如果d(O1,O2)>r2d(O1,O2)>r2 ，那么Pr[h(O1)=h(O2)]≤p2Pr[h(O1)=h(O2)]≤p2

其中，O1,O2∈SO1,O2∈S ，表示两个具有多维属性的数据对象，d(O1,O2)d(O1,O2) 为2个对象的相异程度，也就是1 - 相似度。其实上面的这两个条件说得直白一点，就是当足够相似时，映射为同一hash值的概率足够大；而足够不相似时，映射为同一hash值的概率足够小。

相似度的定义根据实际情况自己决定（有关数据对象相似度的比较，详情可以参考我的另一篇博文：数据相似性的度量方法总结），后面我们可以看到，针对不同的相似度测量方法，局部敏感哈希的算法设计也不同，我们主要看看在两种最常用的相似度下，两种不同的LSH：

1. 使用Jaccard系数度量数据相似度时的min-hash
2. 使用欧氏距离度量数据相似度时的P-stable hash

当然，无论是哪种LSH，其实说白了，都是将高维数据降维到低维数据，同时，还能在一定程度上，保持原始数据的相似度不变。LSH不是确定性的，而是概率性的，也就是说有一定的概率导致原本很相似的数据映射成2个不同的hash值，或者原本不相似的数据映射成同一hash值。这是高维数据降维过程中所不能避免的（因为降维势必会造成某种程度上数据的失真），不过好在LSH的设计能够通过相应的参数控制出现这种错误的概率，这也是LSH为什么被广泛应用的原因。

min-hash

hash函数的选择

了解min-hash之前，首先普及一下Jaccard系数的概念。Jaccard系数主要用来解决的是非对称二元属性相似度的度量问题，常用的场景是度量2个集合之间的相似度，公式这里我不写了，就是2个集合的交比2个集合的并。

比如，我在底下的表格中写出了4个对象（你可以看做是4个文档）的集合情况，每个文档有相应的词项，用词典{w1,w2,…,w7}{w1,w2,…,w7} 表示。若某个文档存在这个词项，则标为1，否则标0.

word	D1D1	D2D2	D3D3	D4D4
w1w1	1	0	1	0
w2w2	1	1	0	1
w3w3	0	1	0	1
w4w4	0	0	0	1
w5w5	0	0	0	1
w6w6	1	1	1	0
w7w7	1	0	1	0

首先，我们现在将上面这个word-document的矩阵按行置换，比如可以置换成以下的形式：

word	D1D1	D2D2	D3D3	D4D4
w2w2	1	1	0	1
w1w1	1	0	1	0
w4w4	0	0	0	1
w3w3	0	1	0	1
w7w7	1	0	1	0
w6w6	1	1	1	0
w5w5	0	0	0	1

可以确定的是，这没有改变文档与词项的关系。现在做这样一件事：对这个矩阵按行进行多次置换，每次置换之后，统计每一列（其实对应的就是每个文档）第一个不为0的位置（行号），这样每次统计的结果能构成一个与文档数等大的向量，这个向量，我们称之为签名向量。

比如，如果对最上面的矩阵做这样的统计，得到[1,2,1,2][1,2,1,2] ，对于下面的矩阵做统计，得到[1,1,2,1][1,1,2,1] .

简单来想这个问题，就拿上面的文档来说，如果两个文档足够相似，那也就是说这两个文档中有很多元素是共有的，换句话说，这样置换之后统计出来的签名向量，如果其中有一些文档的相似度很高，那么这些文档所对应的签名向量的相应的元素，值相同的概率就很高。

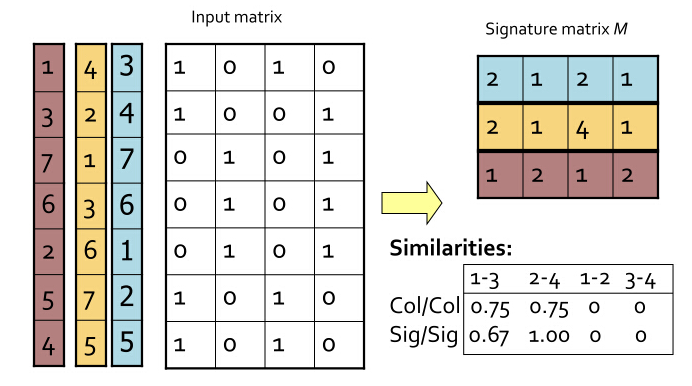
我们把最初始时的矩阵叫做input matrix，由mm 个文档，nn 个词项组成。而把由tt 次置换后得到的一个t×mt×m 的矩阵叫做signature matrix.

下面是我盗的一张图，能够很清晰的展现出这一套流程：

图中，4个文档，做了3次置换，得到了一个3 x 4的签名矩阵。感谢提供图的这篇博文的作者：http://blog.sina.com.cn/s/blog_4ff49c7e0102vl52.html

需要注意的是，置换矩阵的行，在代码实现的时候，可以用这样的算法实现：

1. 在当下剩余的行中（初始时，剩余的行为全部行），随机选取任意一行，看看这一行哪些位置（这里的位置其实是列号）的元素是1，如果签名向量中这个位置的元素还未被写入，则在这个位置写入随机选取的这个行的行号。并将这一行排除。

2. 持续进行1步的工作，直到签名向量全部被写满为止。

以上2步的意义跟对整个矩阵置换、再统计，结果是一样的。这么说可能有点抽象，我把函数放在下面：

def sigGen(matrix):
    """
    * generate the signature vector

    :param matrix: a ndarray var
    :return a signature vector: a list var
    """

    # the row sequence set
    seqSet = [i for i in range(matrix.shape[0])]

    # initialize the sig vector as [-1, -1, ..., -1]
    result = [-1 for i in range(matrix.shape[1])]

    count = 0

    while len(seqSet) > 0:

        # choose a row of matrix randomly
        randomSeq = random.choice(seqSet)

        for i in range(matrix.shape[1]):

            if matrix[randomSeq][i] != 0 and result[i] == -1:
                result[i] = randomSeq
                count += 1
        if count == matrix.shape[1]:
            break

        seqSet.remove(randomSeq)

    # return a list
    return result

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33

现在给出一个定理。

定理：对于签名矩阵的任意一行，它的两列元素相同的概率是xnxn ，其中xx 代表这两列所对应的文档所拥有的公共词项的数目。而xnxn 也就是这两个文档的Jaccard系数。

这个定理我想不用证明了。实际上，置换input matrix的行，取每列第一个非0元的做法，就是一个hash函数。这个hash函数成功地将多维数据映射成了一维数据。而从这个定理我们发现，这样的映射没有改变数据相似度。

需要注意的一点是，这里的hash函数只能对Jaccard系数定义数据相似度的情况起作用。不同的相似度模型，LSH是不同的，目前，还不存在一种通用的LSH。

构造LSH函数族

为了能实现前面LSH定义中的2个条件的要求，我们通过多次置换，求取向量，构建了一组hash函数。也就是最终得到了一个signature matrix. 为了控制相似度与映射概率之间的关系，我们需要按下面的操作进行，一共三步。

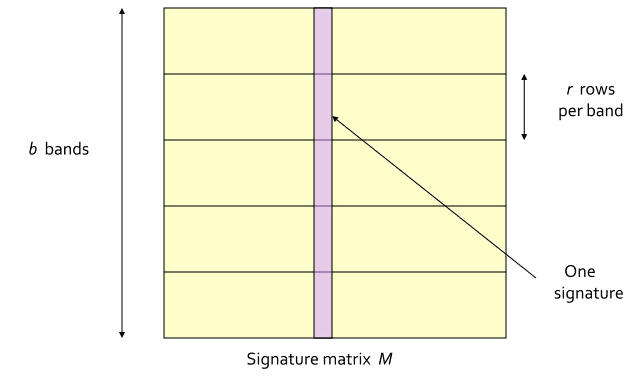
(1) 将signature matrix水平分割成一些区块（记为band），每个band包含了signature matrix中的rr 行。需要注意的是，同一列的每个band都是属于同一个文档的。如下图所示。这个图我还是盗的上面链接中的博文，特此说明。

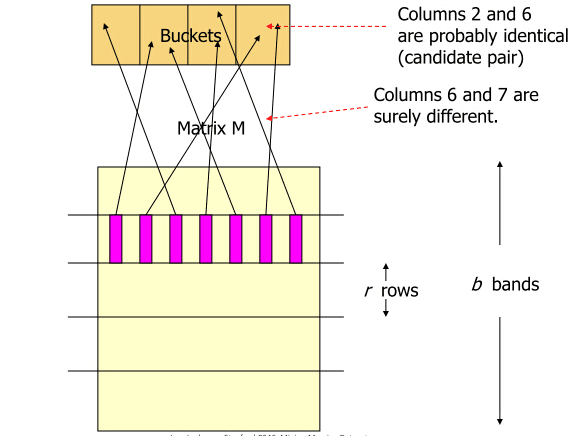
(2) 对每个band计算hash值，这里的hash算法没有特殊要求，MD5，SHA1等等均可。一般情况下，我们需要将这些hash值做处理，使之成为事先设定好的hash桶的tag，然后把这些band“扔”进hash桶中。如下图所示。但是这里，我们只是关注算法原理，不考虑实际操作的效率问题。所以，省略处理hash值得这一项，得到每个band的hash值就OK了，这个hash值也就作为每个hash bucket的tagtag 。

(3) 如果某两个文档的，同一水平方向上的band，映射成了同一hash值（如果你选的hash函数比较安全，抗碰撞性好，那这基本说明这两个band是一样的），我们就将这两个文档映射到同一个hash bucket中，也就是认为这两个文档是足够相近的。

好了，既然执行的是上面三步的操作，那不难计算出两个文档被映射到同一个hash bucket中的概率：

• 对于两个文档的任意一个band来说，这两个band值相同的概率是：srsr ，其中s∈[0,1]s∈[0,1] 是这两个文档的相似度。
• 也就是说，这两个band不相同的概率是1−sr1−sr
• 这两个文档一共存在bb 个band，这bb 个band都不相同的概率是(1−sr)b(1−sr)b
• 所以说，这bb 个band至少有一个相同的概率是1−(1−sr)b1−(1−sr)b

我愿意把这样的方法称为AND then ORAND then OR ，它是先要求每个band的所有对应元素必须都相同，再要求多个band中至少有一个相同。符合这两条，才能发生hash碰撞。

概率1−(1−sr)b1−(1−sr)b 就是最终两个文档被映射到同一个hash bucket中的概率。我们发现，这样一来，实际上可以通过控制参数r,br,b 的值来控制两个文档被映射到同一个哈希桶的概率。而且效果非常好。比如，令b=20,r=5b=20,r=5

• 当s=0.8s=0.8 时，两个文档被映射到同一个哈希桶的概率是：

   
  Pr(LSH(O1)=LSH(O2))=1−(1−0.85)5=0.9996439421094793Pr(LSH(O1)=LSH(O2))=1−(1−0.85)5=0.9996439421094793

• 当s=0.2s=0.2

  时，两个文档被映射到同一个哈希桶的概率是：

   
  Pr(LSH(O1)=LSH(O2))=1−(1−0.25)5=0.0063805813047682Pr(LSH(O1)=LSH(O2))=1−(1−0.25)5=0.0063805813047682

不难看出，这样的设计通过调节参数值，达到了“越相似，越容易在一个哈希桶；越不相似，越不容易在一个哈希桶”的效果。这也就能实现我们上边说的LSH的两个性质。

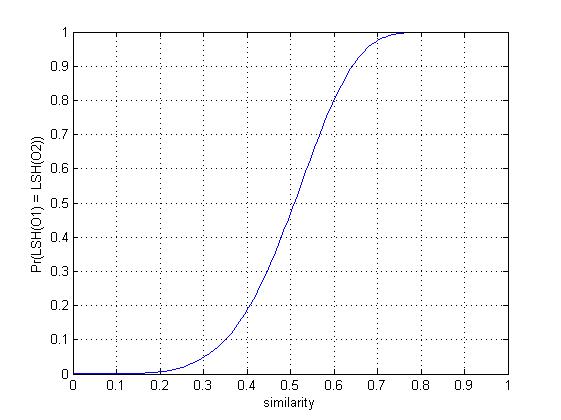
我画出了在r=5,b=20r=5,b=20

参数环境下的概率图，大家会有个更清晰的认识。

当相似度高于某个值的时候，概率会变得非常大，并且快速靠近1，而当相似度低于某个值的时候，概率会变得非常小，并且快速靠近0.

限于篇幅，代码就不在博客里罗列了，需要的话可以访问我的github主页：
https://github.com/guoziqingbupt/Locality-sensitive-hashing
这个项目中，我一共写了min-hash和e2LSH两个算法的实现，min-hash部分请参见模块min_hash.py

另外， 需要注意的是，每一层的band只能和同一层的band相比，若hash值相同，则放入同一个哈希桶中。

P-stable hash

最开始的时候，我们已经说过，不同的相似度判别方法，对应着不同的LSH，那对于最常见的Lp范数下的欧几里得空间，应该用怎样的LSH呢？这就要介绍P-stable hash了。

P-stable distribution

在讲解P-stable hash之前，先简单介绍一下p稳定分布的概念。

定义：一个分布DD

称为pp

稳定分布，如果对于任意n个实数v1,v2,…,vnv1,v2,…,vn

和符合DD

分布的n个独立同分布的随机变量X1,X2,…,XnX1,X2,…,Xn

，都存在一个p≥0p≥0

，使得∑iviXi∑iviXi

和(∑i|vi|p)1/pX(∑i|vi|p)1/pX

具有相同的分布，其中，XX

是一个满足DD

分布的随机变量。

目前，根据相关文献，在p∈(0,2]p∈(0,2]

这个范围内存在稳定分布。我们最常见的是p=1p=1

以及 p=2p=2

时的情况。

• p=1p=1

  时，这个分布就是标准的柯西分布。概率密度函数：c(x)=1π11+x2c(x)=1π11+x2

• p=2p=2

  时，这个分布就是标准的正态分布。概率密度函数：c(x)=12π√e−x2/2c(x)=12πe−x2/2

当然，pp

值不是仅能取1和2. (0,2](0,2]

中的小数也是可以的。

p稳定分布有什么作用呢，我们为什么在这里提出来？它有一个重要的应用，就是可以估计给定向量vv

在欧式空间下的p范数的长度，也就是||v||p||v||p

。

可以这样实现：对于一个向量vv

（相当于上面公式中的(v1,v2,…,vn)(v1,v2,…,vn)

），现在从pp

稳定分布中，随机选取vv

的维度个随机变量（相当于上面公式中的X1,X2,…,XnX1,X2,…,Xn

）构成向量aa

，计算a⋅v=∑iviXia⋅v=∑iviXi

，此时，a⋅va⋅v

与||v||pX||v||pX

同分布。我们就可以通过多给几个不同的向量aa

，多计算几个a⋅va⋅v

的值，来估计||v||p||v||p

的值。

p-stable 分布LSH函数族构造

在p稳定的局部敏感hash中，我们将利用a⋅va⋅v

可以估计||v||p||v||p

长度的性质来构建hash函数族。具体如下：

• 将空间中的一条直线分成长度为rr

  的，等长的若干段。

• 通过一种映射函数（也就是我们要用的hash函数），将空间中的点映射到这条直线上，给映射到同一段的点赋予相同的hash值。不难理解，若空间中的两个点距离较近，他们被映射到同一段的概率也就越高。

• 之前说过，a⋅va⋅v

  可以估计||v||p||v||p

  长度，那么，(a⋅v1−a⋅v2)=a(v1−v2)(a⋅v1−a⋅v2)=a(v1−v2)

  也就可以用来估计||v1−v2||p||v1−v2||p

  的长度。

• 综合上面的3条，可以得到这样一个结论：空间中两个点距离：||v1−v2||p||v1−v2||p

  ，近到一定程度时，应该被hash成同一hash值，而向量点积的性质，正好保持了这种局部敏感性。因此，可以用点积来设计hash函数族。

文献[1]提出了这样一种hash函数族：

 

ha,b(v)=⌊a⋅v+br⌋ha,b(v)=⌊a⋅v+br⌋

其中，b∈(0,r)b∈(0,r)

是一个随机数，rr

是直线的分段长度，hash函数族的函数是依据a,ba,b

的不同建立的。

可见，若要空间中的两个点v1,v2v1,v2

映射为同一hash值，需要满足的条件为：这两点与aa

的点积加上随机值bb

的计算结果在同一条线段上。

现在估计一下这个概率。设c=||v1−v2||pc=||v1−v2||p

，则a⋅v1−a⋅v2a⋅v1−a⋅v2

与cXcX

同分布。概率公式如下：

 

p(c)=Pr[ha,b(v1)=ha,b(v2)]=∫r01cfp(tc)(1−tr)dtp(c)=Pr[ha,b(v1)=ha,b(v2)]=∫0r1cfp(tc)(1−tr)dt

当rr

的值取定的时候，这个公式可以看做是一个仅与cc

的取值相关的函数。cc

越大，函数值越小（碰撞的概率越低）；cc

越小，函数值越大（碰撞的概率越高）。相关的具体证明参见参考文献[2].

但是关于rr

的取值，在文献[1]中，并没有给出一个确定的值。这需要我们根据cc

与pp

的值来设定。

试想，因为我们设定的LSH是(r1,r2,p1,p2)(r1,r2,p1,p2)

敏感的，所以，当r2/r1=cr2/r1=c

的时候（这里的cc

可以看做是一个标准），也就不难推出：p1=p(1),p2=p(c)p1=p(1),p2=p(c)

文献[1]指出，选取合适的rr

值，能够使得ρ=ln(1/p1)ln(1/p2)ρ=ln(1/p1)ln(1/p2)

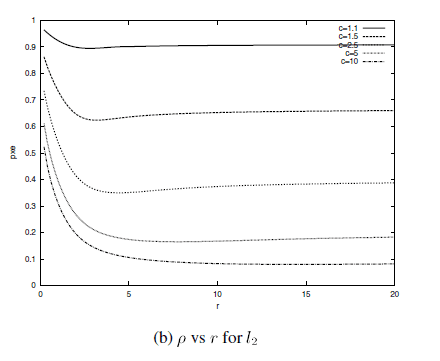
尽可能地小。这里面的理论非常复杂，所以，在这里，我给出文献[1]的一张图：

这是在L2范数下，ρρ

和最优的rr

的关系，可以看出以下几点信息：

1. cc

   的取值不同时，即便对于相同的rr

   ，ρρ

   也不同

2. 在rr

   的取值大于某一点后，ρρ

   对rr

   的变化不再敏感

3. 虽然从图像的趋势上看，rr

   越大，ρρ

   越小，但是，rr

   的取值也不能太大，否则会导致p1,p2p1,p2

   都接近于1，增大搜索时间（我觉得这就导致LSH没意义了）

所以，可见rr

的取值要根据实际情况，自己设定。我有个想法，不知道在具体实施的时候合不合理：可以先确定一下r1,r2r1,r2

的取值，然后选择合适的rr

，使得p1,p2p1,p2

都达到我们的要求即可。

p-stable 分布LSH相似性搜索算法

上面完成了对p-stable 分布LSH函数族构造。那么接下来的问题是怎样具体实现hash table的构造以及查询最近邻。我将这个问题按照本人自己的理解写在下面。因为确实难以找到一个权威的文献具体论述这个问题，虽然文献[3]中讲解了这个问题，但是表达有点模糊不清。所以，下面的内容是我自己的理解，个人觉得问题应该不大，如有错误，请批评指正。

我们构建hash table的过程就是要用这个函数族的每一个函数对每一个向量执行hash运算。为了减少漏报率False Negative（就是本来很相近的两条数据被认为是不相似的），一种解决方案是用多个hash函数对向量执行hash运算，比如说，对任意一个向量vivi

，现在准备了kk

个hash函数(h1(),h2(),…,hk())(h1(),h2(),…,hk())

，这kk

个hash函数是从LSH函数族中随机选取的kk

个，这样，通过计算，就得到了kk

个hash值：(h1(vi),h2(vi),…,hk(vi))(h1(vi),h2(vi),…,hk(vi))

，而对于查询qq

，用同样的kk

个hash函数，也能得到一组值(h1(q),h2(q),…,hk(q))(h1(q),h2(q),…,hk(q))

，这两组值之间，只要有一个对应位的值相等，我们就认为vivi

是查询qq

的一个近邻。

但是，现在有一个问题，那就是上面这种做法的结果，确实减少了漏报率，但与此同时，也增加了误报率（本来不很相近的两条数据被认为是相近的）。所以，需要在上面方法的基础上，再增加一个措施。我们从LSH函数族中，随机选取LL

组这样的函数组，每个函数组都由kk

个随机选取的函数构成，当然LL

个函数组之间不一定是一样的。现在这LL

组函数分别对数据处理，只要有一组完全相等，就认为两条数据是相近的。

其实上面两段的做法，就是一个简单的AND then ORAND then OR

的逻辑，与我们上面说的min-hash的思路是一致的。我本人将这种方法称为是p-stable hash的(k,L)(k,L)

算法。

现在假设P=Pr[ha,b(v1)=ha,b(v2)]P=Pr[ha,b(v1)=ha,b(v2)]

（这个概率可以由上面的积分公式算出），那么，两条数据被认为是近邻的概率是：

 

1−(1−Pk)L1−(1−Pk)L

构建hash table时，如果把一个函数组对向量的一组hash值(h1(vi),h2(vi),…,hk(vi))(h1(vi),h2(vi),…,hk(vi))

作为hash bucket的标识，有两个缺点：1. 空间复杂度大；2. 不易查找。为了解决这个问题，我们采用如下方法：

先设计两个hash函数：H1,H2H1,H2

• H1H1

  ：Zk→{0,1,2,…,size−1}Zk→{0,1,2,…,size−1}

  . 简单说就是把一个kk

  个数组成的整数向量映射到hash table的某一个位上，其中sizesize

  是hash table的长度。

• H2H2

  ：Zk→{0,1,2,…,C}Zk→{0,1,2,…,C}

  . C=232−5C=232−5

  ，是一个大素数。

这两个函数具体的算法如下，其中，ri,r′iri,ri′

是两个随机整数。

 

H1(x1,…,xk)=((∑i=1krixi)modC)modsizeH2(x1,…,xk)=(∑i=1kr′ixi)modCH1(x1,…,xk)=((∑i=1krixi)modC)modsizeH2(x1,…,xk)=(∑i=1kri′xi)modC

我们把H2H2

计算的结果成为一个数据向量的“指纹”，这也好理解，它就是由数据向量的kk

个hash值计算得到的。而H1H1

相当于是数据向量的指纹在hash table中的索引，这个算法跟基本的散列表算法是一个思路，不啰嗦了。

通过这两个新建的函数，我们可以将hash table的构建步骤作以下详细说明：

1. 从设计好的LSH函数族中，随机选取LL

   组hash函数，每组由kk

   个hash函数构成，记为{g1(⋅),g2(⋅),…,gL(⋅)}{g1(⋅),g2(⋅),…,gL(⋅)}

   ，其中gi(⋅)=(h1(⋅),h2(⋅),…,hk(⋅))gi(⋅)=(h1(⋅),h2(⋅),…,hk(⋅))

2. 每个数据向量经过gi(⋅)gi(⋅)

   被映射成一个整型向量，记为(x1,…,xk)(x1,…,xk)

3. 将2步生成的(x1,…,xk)(x1,…,xk)

   通过H1,H2H1,H2

   计算得到两个数值：index,fpindex,fp

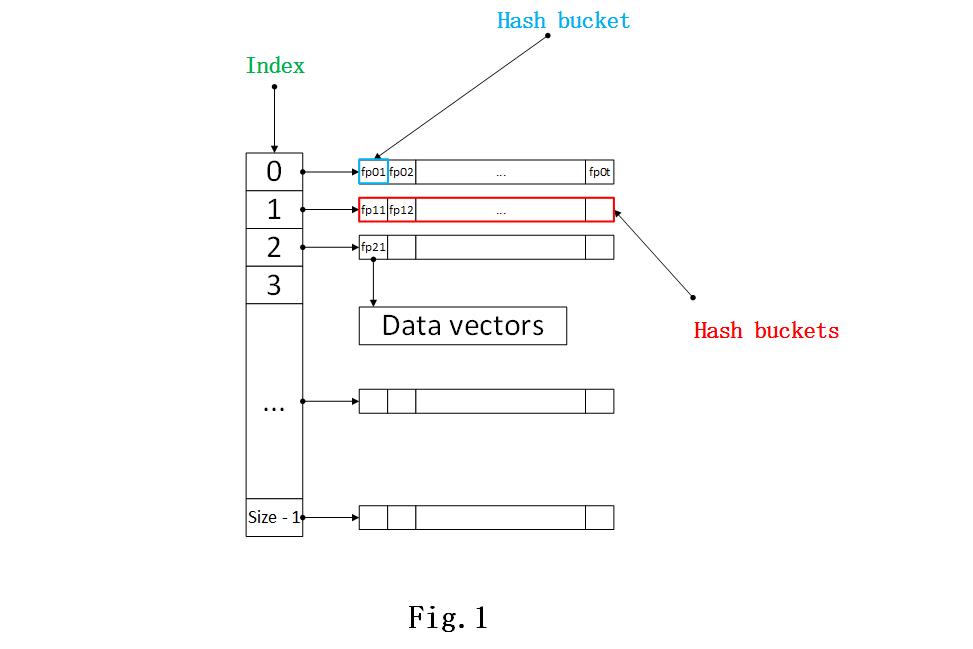
   ，前者是hash table的索引，后者是数据向量对应的指纹。这里，为了方便描述这种hash table的结构，我将我们用的hash table的结构画出，如图Fig.1所示。

4. 若其中有数据向量拥有相同的数据指纹，那么必然会被映射到同一个hash bucket当中

通过Fig.1，就不难理解这里的数据结构了，数据向量由H2H2

生成数据指纹（图中的fp01,fp12fp01,fp12

这些），每个数据指纹就是一个hash bucket的标识，存储着对应的数据向量。

可以得到相同H1(⋅)H1(⋅)

值的hash bucket我们放在一个链表中，这个链表对应的就是hash table中相应的索引。

由于篇幅限制，我在此省略代码，详细的代码实现请参考我的github主页的项目，里面的e2LSH模块写的是p - stable 局部敏感hash的算法：
https://github.com/guoziqingbupt/Locality-sensitive-hashing

本文写的战战兢兢，实在不敢说没有问题，望大家参考，批评指正。

参考文献

[1] Datar M, Immorlica N, Indyk P, et al. Locality-sensitive hashing scheme based on p-stable distributions[C]//Proceedings of the twentieth annual symposium on Computational geometry. ACM, 2004: 253-262.

[2]LSH和p-stable LSH http://blog.sina.com.cn/s/blog_67914f2901019p3v.html

[3]E2LSH源码分析–p稳定分布LSH算法初探
http://blog.csdn.net/jasonding1354/article/details/38237353