LeetCode(119):杨辉三角 II
Easy!
题目描述:
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 3
输出: [1,3,3,1]
进阶:
你可以优化你的算法到 O(k) 空间复杂度吗?
解题思路:
杨辉三角想必大家并不陌生,应该最早出现在初高中的数学中,其实就是二项式系数的一种写法。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
杨辉三角形第n层(顶层称第0层,第1行,第n层即第n+1行,此处n为包含0在内的自然数)正好对应于二项式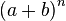 展开的系数。例如第二层1 2 1是幂指数为2的二项式
展开的系数。例如第二层1 2 1是幂指数为2的二项式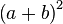 展开形式
展开形式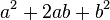 的系数。
的系数。
杨辉三角主要有下列五条性质:
- 杨辉三角以正整数构成,数字左右对称,每行由1开始逐渐变大,然后变小,回到1。
- 第
 行的数字个数为
行的数字个数为 个。
个。 - 第
 行的第
行的第 个数字为组合数
个数字为组合数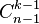 。
。 - 第
 行数字和为
行数字和为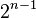 。
。 - 除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和(也就是说,第
 行第
行第 个数字等于第
个数字等于第 行的第
行的第 个数字与第
个数字与第 个数字的和)。这是因为有组合恒等式:
个数字的和)。这是因为有组合恒等式: 。可用此性质写出整个杨辉三角形。
。可用此性质写出整个杨辉三角形。
由于题目有额外限制条件,程序只能使用O(k)的额外空间,那么这样就不能把每行都算出来,而是要用其他的方法,。最先考虑用的是第三条性质,算出每个组合数来生成第n行系数,代码如下:
C++ 解法一:
/**
* NOT Correct!
*/
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> out;
if (rowIndex < ) return out; for (int i = ; i <= rowIndex; ++i) {
if ( i == || i == rowIndex)
out.push_back();
else
out.push_back (computeCnk(rowIndex, i));
}
return out;
} int computeCnk(int n, int k) {
if (k > n) return ;
else if (k > n/) k = n - k;
int numerator = , denomator = ;
for (int i = ; i < k; ++i) {
numerator *= n - i;
denomator *= k - i;
}
if (denomator != ) return numerator/denomator;
else return ;
}
};
本地调试输出前十行,没啥问题,拿到OJ上测试,程序在第18行跪了,中间有个系数不正确。那么问题出在哪了呢,仔细找找,原来出在计算组合数那里,由于算组合数时需要算连乘,而整形数int的数值范围只有-32768到32768之间,那么一旦n值过大,连乘肯定无法计算。而丧心病狂的OJ肯定会测试到成百上千行,所以这个方法不行。那么我们再来考虑利用第五条性质,除了第一个和最后一个数字之外,其他的数字都是上一行左右两个值之和。那么我们只需要两个for循环,除了第一个数为1之外,后面的数都是上一次循环的数值加上它前面位置的数值之和,不停地更新每一个位置的值,便可以得到第n行的数字。
C++ 解法二:
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> out;
if (rowIndex < ) return out;
out.assign(rowIndex + , );
for (int i = ; i <= rowIndex; ++i) {
if ( i == ) {
out[] = ;
continue;
}
for (int j = rowIndex; j >= ; --j) {
out[j] = out[j] + out[j-];
}
}
return out;
}
};
LeetCode(119):杨辉三角 II的更多相关文章
- Java实现 LeetCode 119 杨辉三角 II
119. 杨辉三角 II 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 3 输出: [1,3,3,1] 进阶: ...
- LeetCode(119. 杨辉三角 II)
问题描述 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 3 输出: [1,3,3,1] 进阶: 你可以优化你的 ...
- 【LeetCode】119. 杨辉三角 II Pascal‘s Triangle II(Python & Java)
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题思路 方法一: 空间复杂度 O ( k ∗ ( k + 1 ...
- 119.杨辉三角II
这道题和第118题是一样的,需要注意这道题目对行数的要求 # 定义一个列表,用来存放数据 num_list = [] for index1 in ran ...
- 力扣119. 杨辉三角 II
原题 1 class Solution: 2 def getRow(self, rowIndex: int) -> List[int]: 3 ans = [1] 4 for i in range ...
- LeetCode119.杨辉三角 II
119.杨辉三角 II 描述 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例 输入: 3 输出: [1,3,3,1] 进阶 ...
- LeetCode:杨辉三角【118】
LeetCode:杨辉三角[118] 题目描述 给定一个非负整数 numRows,生成杨辉三角的前 numRows 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 5 输出: ...
- [LeetCode] 119. Pascal's Triangle II 杨辉三角 II
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- LeetCode 118:杨辉三角 II Pascal's Triangle II
公众号:爱写bug(ID:icodebugs) 作者:爱写bug 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行. Given a non-negative index k whe ...
随机推荐
- Flume配置Load balancing Sink Processor
1 官网内容 2 找一个图来理解一目了然 3 详细配置 配置文件load_source_case.conf 配置数据入口 source到channel 配置了两个sink用来做负载均衡 #配置文件: ...
- springboot-全局异常处理类
@ControllerAdvice public class GlobalExceptionHandler(){ @ExceptionHandler(value=Exception.class) @R ...
- 【blog】推荐一个博客系统后台管理模板 - pinghsu
pinghsu https://github.com/chakhsu/pinghsu
- pycharm 使用教程
本文为大家讲解的是pycharm 的安装和首次使用,PyCharm 是我用过的python编辑器中,比较顺手的一个.而且可以跨平台,在macos和windows下面都可以用,这点比较好.感兴趣的同学参 ...
- python - 文件系统和文件
文件系统和文件 文件系统是os用于明确磁盘或分区上的文件的方法和数据结构--即在磁盘上组织文件的方法 计算机文件,是存储在某种长期储存设备或临时存储设备中的一段数据流,并且 ...
- vue 中通过 ajax 获取数据时,如何避免绑定的数据中出现 property of undefined 错误
参考链接:https://segmentfault.com/q/1010000008264089?_ea=1597485
- 接口转换 数据库列表的内容 显示在datagrid
public class AddressConverter : IValueConverter { public object Convert(object value, Type targetTyp ...
- 在Linux环境下使用Apache部署ASP.NET Core
在前几篇文章中我们一起探讨了如何在Linux环境中安装ASP.NET Core运行时环境及将ASP.NET Core项目部署在Jexus中,这篇文章中我们将探讨如何将ASP.NET Core部署于Ap ...
- 从无文件技术到使用隐写术:检查Powload的演变
来源:https://blog.trendmicro.com/trendlabs-security-intelligence/from-fileless-techniques-to-using-ste ...
- python3-深浅copy
转载:https://www.cnblogs.com/ctztake/p/8194275.html 术语 变量:是一个系统表的元素,拥有指向对象的连接空间. 对象:被分配的一块内存,存储其所代表的值. ...
