RNN
在DNN中，当前输出层的值只和当前输入值有关系。如果当前输出值不仅依赖当前输入值，也依赖于前面时刻的输入值，那么DNN就不适用了。因此也就有了RNN。
一、RNN结构
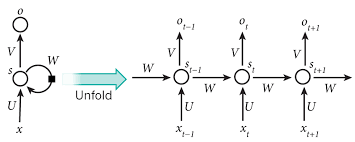
这是最简单的RNN。其中Xt是t时刻的输入，S是隐藏层。Ot是t时刻的输出。隐藏层St是由前t-1个时刻的隐藏层叠加而成的。把St也可以理解为前t时刻x的记忆叠加而成的隐藏层。
二、RNN的前向传播
1、记
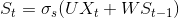
其中σs为激活函数。W是隐藏层S上的权重，如上式所示，作用跟输入一起来迭代S。
2、
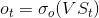
其中σt为激活函数
ot为t时刻的输出也是叠加了了t-1之前时刻输入的输出
U为输入层的权重
V为隐藏层到输出层的权重
三、 RNN的反向传播（BPTT，back-propagation through time）
为了学习，假设σs为tanh函数，σt为softmax函数。
求参的过程还是和大多数学过的模型求参一样，列出损失函数，例如MSE，交叉熵等，然后用最大似然估计求参数形式，再用SGD随机梯度下降求解。
这里面需要求U、W、V。
1、
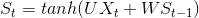
2、
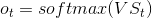
3、损失函数，在图中，在unfold里面，由于每一点都有一个o，因此每一点都有一个损失。因此总的损失就是每一点损失之和。
4、记
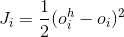
oh为模型输出值，没有上标h的o为真实值。
5、对V求导
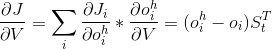
6、对W求导。
（1）
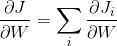
（2）
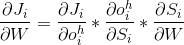
（3）由于
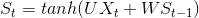
（4）为了解下计算过程，简单起见，设i=2
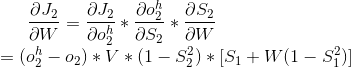
以次类推。
7、对U求导
（1）
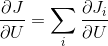
（2）
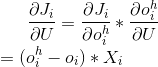
8、有了每个参数的梯度，然后利用SGD可以更新参数了。
RNN的更多相关文章
- RNN求解过程推导与实现
RNN求解过程推导与实现 RNN LSTM BPTT matlab code opencv code BPTT,Back Propagation Through Time. 首先来看看怎么处理RNN. ...
- 在RNN中使用Dropout
dropout在前向神经网络中效果很好,但是不能直接用于RNN,因为RNN中的循环会放大噪声,扰乱它自己的学习.那么如何让它适用于RNN,就是只将它应用于一些特定的RNN连接上. LSTM的长期记 ...
- RNN 入门学习资料整理
建议按序阅读 1. RNN的一些简单概念介绍 A guide to recurrent neural networks and backpropagation Deep learning:四十九(RN ...
- lecture7-序列模型及递归神经网络RNN
Hinton 第七课 .这里先说下RNN有recurrent neural network 和 recursive neural network两种,是不一样的,前者指的是一种人工神经网络,后者指的是 ...
- RNN 入门教程 Part 4 – 实现 RNN-LSTM 和 GRU 模型
转载 - Recurrent Neural Network Tutorial, Part 4 – Implementing a GRU/LSTM RNN with Python and Theano ...
- RNN 入门教程 Part 3 – 介绍 BPTT 算法和梯度消失问题
转载 - Recurrent Neural Networks Tutorial, Part 3 – Backpropagation Through Time and Vanishing Gradien ...
- RNN 入门教程 Part 2 – 使用 numpy 和 theano 分别实现RNN模型
转载 - Recurrent Neural Networks Tutorial, Part 2 – Implementing a RNN with Python, Numpy and Theano 本 ...
- RNN 入门教程 Part 1 – RNN 简介
转载 - Recurrent Neural Networks Tutorial, Part 1 – Introduction to RNNs Recurrent Neural Networks (RN ...
- CNN & RNN 及一些常识知识（不断扩充中）
参考: http://blog.csdn.net/iamrichardwhite/article/details/51089199 一.神经网络的发展历史 五六十年代,提出感知机 八十年代,提出多层感 ...
- 循环神经网络(RNN, Recurrent Neural Networks)介绍（转载）
循环神经网络(RNN, Recurrent Neural Networks)介绍 这篇文章很多内容是参考:http://www.wildml.com/2015/09/recurrent-neur ...
随机推荐
- js常见的排序算法
最近面试可能会问这些 1,插入排序 function sort(elements){ var res =[elements[0]]; for (var i = 0; i < elements.l ...
- 解题：CF622F The Sum of the k-th Powers
题面 TJOI2018出CF原题弱化版是不是有点太过分了?对,就是 TJOI2018 教科书般的亵渎 然而我这个问题只会那个题的范围的m^3做法 回忆一下1到n求和是二次的,平方求和公式是三次的,立方 ...
- webpack 非严格模式设置 npm i babel-plugin-transform-remove-strict-mode
安装插件:npm i babel-plugin-transform-remove-strict-mode 在.babelrc文件的插件项添加:"transform-remove-strict ...
- C#项目获取当前时间的农历时间
https://blog.csdn.net/cstester/article/details/7407044 using System.Globalization; class CnCanlendar ...
- mongodb安装和运行
转载来源:https://blog.csdn.net/IT_wanghe/article/details/53884229 参考教程:http://www.runoob.com/mongodb/mon ...
- cmd代码：查端口占用，查进程号，杀进程
@echo off :main cls ::|findstr "8080" ::查找进程占用tasklist|findstr "XXXX" ::杀进程taskk ...
- springboot 新模板 呵呵了
<html> <head> <title>批处理任务管理</title> <meta name="decorator" con ...
- Luogu P4097 [HEOI2013]Segment 李超线段树
题目链接 \(Click\) \(Here\) 李超线段树的模板.但是因为我实在太\(Naive\)了,想象不到实现方法. 看代码就能懂的东西,放在这里用于复习. #include <bits/ ...
- python csv与字典操作
# encoding: utf-8 import csv d1 = {'banana':3,'apple':4,'pear':1,'orange':2} d2 = {'banana':3,'orang ...
- Numpy 笔记: 多维数组的切片(slicing)和索引(indexing)【转】
目录 切片(slicing)操作 索引(indexing) 操作 最简单的情况 获取多个元素 切片和索引的同异 切片(slicing)操作 Numpy 中多维数组的切片操作与 Python 中 lis ...