【XSY2753】Lcm 分治 FWT FFT 容斥

题目描述

　　给你\(n,k\)，要你选一些互不相同的正整数，满足这些数的\(lcm\)为\(n\)，且这些数的和为\(k\)的倍数。

　　求选择的方案数。对\(232792561\)取模。

　　\(n\leq {10}^{18},k\leq 20\)，\(n\)的全部质因子都\(\leq 100\)

题解

解法一

　　一个\(\leq {10}^{18}\)的数最多有\(15\)不同的质因子。

　　记\(w=15,m=2^w=32768\)

　　先看看这个模数有什么特点。

　　\(p=232792561=lcm(1,2,\ldots,20)+1\)

　　这告诉我们可以对长度在\(1\ldots 20\)的区间DFT。

　　所以可以在所有用到模\(k\)的余数的地方DFT，然后对于每个余数做要做的事情。

　　对于一个数，如果这个数的某个质因子的最高次幂\(\neq n\)的这个质因子的最高次幂，这个质因子是没有用的。

　　这样可以把一个数\(x\)表示成一个数对\(g(x)=(i,j)\)，其中\(i\)是一个状态，表示\(x\)有哪些质因子的最高次幂和\(n\)的最高次幂相同。\(j\)表示这个数模\(k\)的余数。

　　先暴力枚举所有\(n\)的因子（\(\approx {10}^5\)个），记\(a_{i,j}\)表示有多少个数\(x\)对应的数对\(g(x)=(i,j)\)。

　　现在对于每一个\(i\)，计算只取这些数，和模\(k\)为\(j=0\ldots k-1\)的方案数\(f_{i,j}\)。

　　记\(F_i(x)=\sum_{i=0}^{k-1}f_{i,j}x^j\)，那么有\(F_i(x)=\prod_{i=0}^{k-1}{(1+x^i)}^{a_{i,j}}\mod x^k\)。（当然你也可以用一些其他的方法计算，比如说每加一个数进去就维护一下）

　　算出\(F_i(x)\)之后做一遍DFT，这样各个\(j\)之间就互不影响了。在做完接下来的步骤后IDFT回来，然后取\(j=0\)的值就是答案了。

　　剩下的步骤我们认为\(k=1\)，即不考虑模\(k\)的余数。

　　现在我们要取一些\(i\)出来，满足\(i_1~or~i_2~or,\cdots,or~i_m\)，把答案加上\(f_{i_1}f_{i_2}\cdots f_{i_m}\)。

　　令\(g_{i,j}=\begin{cases}f_i&j=i\\0&j\neq i\end{cases}\)，那么我们要求的答案就是一个类似\(g_1\oplus g_2\oplus\cdots\oplus g_m\)的东西（实际上在DFT之前\(g_{i,0}\)要\(+1\)表示不选，DFT之后每一位都要\(+1\)）。这里\(\oplus\)是集合或卷积。

　　直接做的复杂度是\(O(w4^w)\)，太慢了。

　　注意到\(g_i\)只有一项非零，所以可能有更快的做法。

　　考虑分治，观察怎么把两个状态合并。

　　合并的时候记左边的结果为

　　\(A_1\)，右边的结果为\(A_2\)，那么合并之后的就是\(A_1+A_2+A_1A_2\)。

　　合并的两个数组是长这样的：

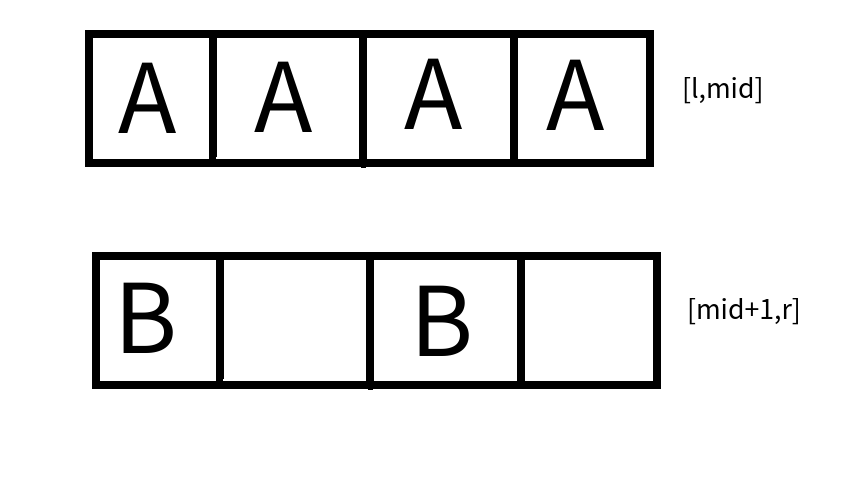
　　整个数组是一个部分重复很多次。

![](https://images2018.cnblogs.com/blog/1097689/201803/1097689-20180319083442163-80799273.png）

　　我们可以只储存&计算循环节部分，要用更长的部分的时候再扩展。

　　另一种理解是：每个\(g_{i,j}\)对答案的\(s_l(j\subseteq l)\)都有贡献，这个贡献是乘上去的（因为是在FWT后对应位乘起来）。

　　因为前面已经做过一次求幂了（\(F_i(x)\)），所以你也可以这几步先不做（求幂和乘法），在最后做一次求幂。这个就是下面的容斥做法。

　　总时间复杂度是\(O(k^22^w+kw2^w)\)

解法二

　　一个容斥的做法。

　　记\(g_{i,j}\)为有多少个数满足：对于\(i\)中每个\(1\)的二进制位，这些位对应的质因子的次数要取到上限，剩下位的可以任意取，且这个数模\(k\)为\(j\)。

　　\(G_i(x)=\sum_{j=0}^{k-1}{(1+x^j)}^{g_{i,j}}\)

　　然后容斥一下，容斥过程就是IFWT。

　　那么把这个东西做一遍IFWT就是答案了。

　　时间复杂度和上面的差不多。

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int p=232792561;
const int root=71;
ll fp(ll a,ll b)
{
	ll s=1;
	for(;b;b>>=1,a=a*a%p)
		if(b&1)
			s=s*a%p;
	return s;
}
int w[1010];
int w2[1010];
ll n;
int m,k,cnt;
ll a[200010];
int d[100];
int c[100];
ll e[100];
int all;
void dft(int *a,int n)
{
	static int b[100];
	for(int i=0;i<n;i++)
		b[i]=0;
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			b[i]=(b[i]+(ll)a[j]*w[i*j])%p;
	for(int i=0;i<n;i++)
		a[i]=b[i];
}
void idft(int *a,int n)
{
	static int b[100];
	for(int i=0;i<n;i++)
		b[i]=0;
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			b[i]=(b[i]+(ll)a[j]*w2[i*j])%p;
	int inv=fp(n,p-2);
	for(int i=0;i<n;i++)
		a[i]=(ll)b[i]*inv%p;
}
void getfactor(int x,ll s)
{
	if(x>m)
	{
		a[++cnt]=s;
		return;
	}
	for(int i=0;i<=d[x];i++,s*=c[x])
		getfactor(x+1,s);
}
int f[50000][20];
int g[50000][20];
void gao(int x,int y,int s)
{
	if(x==0)
	{
//		for(int i=0;i<k;i++)
//			f[y][i]=b[s][i];
//		dft(f[y],k);
//		idft(f[y],k);
		return;
	}
	gao(x-1,y,s);
	gao(x-1,y+(1<<(x-1)),s|(1<<(x-1)));
	for(int i=y+(1<<(x-1));i<y+(1<<x);i++)
		for(int j=0;j<k;j++)
		{
			g[i][j]=f[i][j];
			f[i][j]=f[i-(1<<(x-1))][j];
//			f[i][j]=1;
		}
	for(int i=y;i<y+(1<<(x-1));i++)
		for(int j=0;j<k;j++)
//			g[i][j]=1;
			g[i][j]=0;
	for(int i=y;i<y+(1<<x);i++)
		for(int j=0;j<k;j++)
			f[i][j]=(f[i][j]+g[i][j]+(ll)f[i][j]*g[i][j])%p;
}
void add(int x,int y)
{
	static int c[20];
	for(int i=0;i<k;i++)
		c[i]=f[x][i];
	for(int i=0;i<k;i++)
		f[x][(i+y)%k]=(f[x][(i+y)%k]+c[i])%p;
	f[x][y]=(f[x][y]+1)%p;
}
void solve()
{
	scanf("%lld%d",&n,&k);
	w[0]=1;
	ll rt=fp(root,(p-1)/k);
	for(int i=1;i<=1000;i++)
		w[i]=(ll)w[i-1]*rt%p;
	for(int i=0;i<=1000;i++)
		w2[i]=fp(w[i],p-2);
	m=0;
	for(int i=2;i<=100;i++)
		if(n%i==0)
		{
			m++;
			c[m]=i;
			d[m]=0;
			e[m]=1;
			while(n%i==0)
			{
				n/=i;
				d[m]++;
				e[m]*=i;
			}
		}
	cnt=0;
	getfactor(1,1);
	memset(f,0,sizeof f);
	for(int i=1;i<=cnt;i++)
	{
		int s=0;
		for(int j=1;j<=m;j++)
			if(a[i]%e[j]==0)
				s|=1<<(j-1);
		add(s,a[i]%k);
	}
	for(int i=0;i<1<<m;i++)
	{
		f[i][0]++;
		dft(f[i],k);
	}
//	gao(m,0,0);
	for(int i=1;i<1<<m;i<<=1)
		for(int j=0;j<1<<m;j++)
			if(j&i)
				for(int l=0;l<k;l++)
					f[j][l]=(ll)f[j][l]*f[j-i][l]%p;
//	for(int j=1;j<1<<m;j<<=1)
//		for(int l=0;l<1<<m;l++)
//			if(j&l)
//				for(int i=0;i<k;i++)
//					f[l][i]=(f[l][i]-f[l-j][i])%p;
	int all=(1<<m)-1;
	for(int i=0;i<all;i++)
	{
		int v=1;
		for(int j=0;j<m;j++)
			if(!((i>>j)&1))
				v=-v;
		for(int j=0;j<k;j++)
			f[all][j]=(f[all][j]+v*f[i][j])%p;
	}
	idft(f[all],k);
	ll ans=f[all][0];
	ans=(ans+p)%p;
	printf("%lld\n",ans);
}
int main()
{
#ifndef ONLINE_JUDGE
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
#endif
	int t;
	scanf("%d",&t);
	while(t--)
		solve();
	return 0;
}