网络流相关知识点以及题目//POJ1273 POJ 3436 POJ2112 POJ 1149

首先来认识一下网络流中最大流的问题

给定一个有向图G＝（V，E），把图中的边看做成管道，边权看做成每根管道能通过的最大流量（容量），给定源点s和汇点t，在源点有一个水源，在汇点有一个蓄水池，问s－t的最大水流量是多少

网络流图里,源点流出的量等于汇点流入的量,除源汇外的任何点,其流入量之和等于流出量之和 。

首先我们来看下面的图

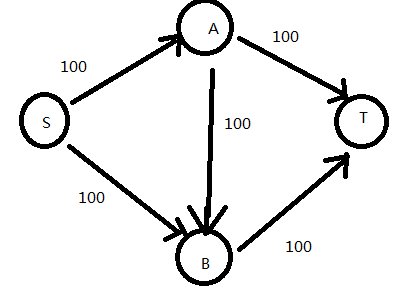
s是源点,t是汇点

先这么想,先用dfs找出一条从s-t的路线,把他塞满,然后流量就是路径中容量最小的那条路的容量,然后把路径上的容量都剪去这个流量,再重新从s-t找可行路径,直到找不到为止

用这种思路看这个图

先走S-A-B-T,这样流量为100,并且没有可行路径了,即操作结束.

可是很明显,从S-A-T,S-B-T这两条路加起来的流量为200。所以这种思路是错的。

主要是过早的认为A-B的流量不为0

改进的思路：建立一个可以修改的网络，使得不合理的流可以被删掉

一种实现：对上次dfs时找到的流量路径上的边，添加一条“反向”边，反向边上的容量等于上次dfs时找到的该边上的流量，然后再利用“反向”的容量和其他边上剩余的容量寻找路径。

使用这种思路再求一次

第一次dfs后

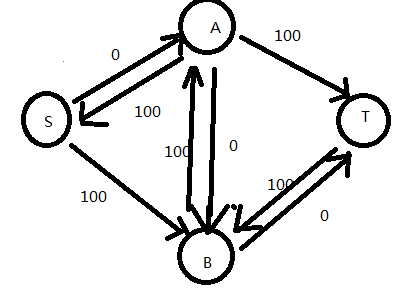
第二次dfs（为了方便把容量为0的边删了）

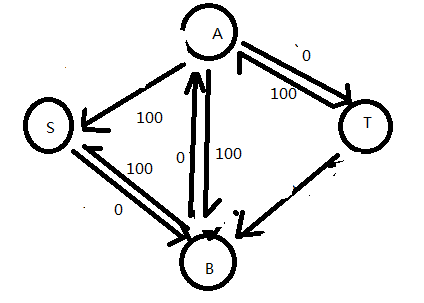
这个时候已经没有可以走的边了，流量为200，dfs结束

为什么这种思路是正确的呢，网上有不少详细的证明。

Ford-Fulkerson算法
就是用这种思路做的

用dfs求增广路径，每次找到之后处理，直到找不到为止。

假设有n个定点，m条边，那么dfs的复杂度为n+m；

dfs运行c次

所以复杂度为c*(n+m);

但是dfs可能会运行很多次。

比如上面的图如果A-B中有条容量为1的边，那么运气不好的话，能执行200次dfs；

但实际上只要用2次就能找到

在每次增广的时候，选择从源到汇的具有最少边数的增广路径,即不是通过dfs寻找增广路径，而是通过bfs寻找增广路径。
这就是Edmonds-Karp 最短增广路算法
已经证明这种算法的复杂度上限为nm2 (n是点数， m是边数）；

现在来说几道题目

1-〉POJ 1273

题意:网络流的裸题，1为源点，n为汇点，给定每条边的容量，求最大流，用EK算法

1273

Accepted

1052K

0MS

G++

1430B

 #include <stdio.h>
 #include <iostream>
 #include <stdlib.h>
 #include <string.h>
 #include <algorithm>
 #include <vector>
 #include <queue>
 using namespace std;
 #define N 300
 #define INF 0x7fffffff
 int Map[N][N];
 int path[N];
 //bool vis[N];
 int n,m;
 bool bfs(int s,int t)
 {
     int p;
     queue<int> q;
     memset(path,-,sizeof(path));
    //memset(vis,false,sizeof(vis));
     path[s]=s;
    // vis[s]=true;
     q.push(s);
     while(!q.empty())
     {
         p=q.front();
         q.pop();
         for(int i=;i<=n;i++)
         {
             if(Map[p][i]>&&path[i]==-)
             {
                 path[i]=p;
                 //vis[i]=true;
                 if(i==t)
                     return true;
                 q.push(i);
             }
         }
     }
     return false;
 }
 int EK(int s,int t)
 {
     int flow=;
     int d;
     int i;
     while(bfs(s,t))
     {
         d=INF;
         for(i=t;i!=s;i=path[i])
         {
             d=min(d,Map[path[i]][i]);
         }
         for(i=t;i!=s;i=path[i])
         {
             Map[path[i]][i]-=d;
             Map[i][path[i]]+=d;
         }
         flow+=d;
     }
     return flow;
 }
 int main()
 {
     while(scanf("%d %d",&m,&n)!=EOF)
     {
         memset(Map,,sizeof(Map));
         for(int i=;i<=m;i++)
         {
             int from,to,flow;
             scanf("%d %d %d",&from,&to,&flow);
             Map[from][to]+=flow;
         }
         printf("%d\n",EK(,n));
     }

     return ;
 }

2-〉POJ 3436

题意：一台电脑有P个部分，当电脑所有部分都被修好的时候，这台电脑才能出厂，有N台机器，每台机器每天最多能处理Q台电脑，机器只能接收与要求相符合的电脑，0表示这个部件不能有，1表示这个部件必须有，2表示这个部件可有可无，机器接受电脑部件之后会产出相应的产品，1表示这个部件有，0表示这个部件没有。求工厂一天能出厂多少台电脑。

思路：拆点建图，把接收形如222，000。。。（只要其中没有1），就把源点向这个点连一条容量为无穷大的边，把产出为111的，就把这个点向汇点连一条无穷大的边，我把编号为i的点，那么这个点拆成2*i-1和2*i两个点，2*i-1代表接受的，2*i代表产出的，这两个点之间连一条容量为第i台机器每天处理的电脑量的边，如果某台机器产出的点符合令一台机器接受的点，那就把那两个点也连上一条容量为无穷大的边。之后求最大流就可以了。

3436

Accepted

8648K

32MS

G++

3338B

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <queue>
 #include <stdlib.h>
 #include <stack>
 using namespace std;
 #define N 1000
 #define INF 0x7fffffff
 int pre[N];
 int map[N][N];
 int mmap[N][N];
 int P,n;
 struct node
 {
     int rec[N];
     int pro[N];
     int flow;
 };
 node mac[N];
 bool bfs(int s,int t)
 {
     int p;
     stack<int> q;//不知道为什么stack能过queue就wa了。。
     memset(pre,-,sizeof(pre));
     pre[s]=s;
     q.push(s);
     while(!q.empty())
     {
         p=q.top();
         q.pop();
         for(int i=;i<=*n+;i++)
         {
             if(map[p][i]>&&pre[i]==-)
             {
                 pre[i]=p;
                 if(i==t)
                     return true;
                 q.push(i);

             }
         }
     }
     return false;
 }
 void EK(int s,int t)
 {
     int flow=;
     int d,i;
     int cnt=;
     while(bfs(s,t))
     {
         d=INF;
         for(i=t;i!=s;i=pre[i])
             d=min(d,map[pre[i]][i]);
         for(i=t;i!=s;i=pre[i])
         {
             map[pre[i]][i]-=d;
             if(!mmap[pre[i]][i])
             {
                 if(pre[i]%==&&i&&&i!=t&&pre[i]!=)
                 {

                     cnt++;
                 }
             }
             map[i][pre[i]]+=d;
             mmap[pre[i]][i]+=d;//每台机器之间流过的电脑数量
         }

         flow+=d;
     }
     printf("%d %d\n",flow,cnt);//最大流就是最多能产出的电脑，cnt就是几条机器之间的路径
     for(int i=;i<=*n;i++)
         for(int j=;j<=*n;j++)
         {
             if(mmap[i][j]&&i%==&&j%!=)
             {
                 printf("%d %d %d\n",i/,(j+)/,mmap[i][j]);
             }
         }
 }
 int main()
 {
     while(scanf("%d %d",&P,&n)!=EOF)
     {
         int cnt=;
         memset(map,,sizeof(map));
         memset(mmap,,sizeof(mmap));
         for(int i=;i<=n;i++)
         {
             scanf("%d",&mac[i].flow);
             for(int j=;j<=P;j++)scanf("%d",&mac[i].rec[j]);
             for(int j=;j<=P;j++)scanf("%d",&mac[i].pro[j]);
             map[cnt][cnt+]=mac[i].flow;//拆点
             cnt+=;
         }
         bool flag;
         for(int i=;i<=n;i++)//处理源点和汇点
         {
             bool flag1=true;
             bool flag2=true;
             for(int j=;j<=P;j++)
                 if(mac[i].pro[j]==)flag2=false;
             if(flag2)
                 map[i*][*n+]=INF;
             flag1=true;
             flag2=true;
             for(int j=;j<=P;j++)
                 if(mac[i].rec[j]==)flag1=false;
             if(flag1)
                 map[][*i-]=INF;
         }
         for(int i=;i<=n;i++)//每台机器之间连边
         {
             for(int j=;j<=n;j++)
             {
                 if(i==j)
                     continue;
                 for(int k=;k<=P;k++)
                 {
                     flag=true;
                     if((mac[i].pro[k]==&&mac[j].rec[k]==)||(mac[i].pro[k]==&&mac[j].rec[k]==))
                     {
                         flag=false;
                         break;
                     }
                 }
                 if(flag)
                 {
                     int u=i*;
                     int v=j*-;
                     map[u][v]=INF;
                 }
             }
         }

        /* for(int i=0;i<=2*n+1;i++)
         {
             for(int j=0;j<=2*n+1;j++)
             {
                 printf("i:%d j:%d map[i][j]=%d\n",i,j,map[i][j]);
             }
         }*/
         EK(,*n+);
     }
     return ;
 }

3-> POJ 2112

题意：有k个挤奶机编号为1-k，有c个奶牛编号为k＋1-k+c，奶牛和挤奶机之间有路径（没有路径给出来的距离是0），一个挤奶机每天可以处理M头奶牛
求出需要走最大距离去挤奶的牛的路径最小值
思路：先用floyd求出每个牛到每个挤奶机的最小路径，问题就转化成了已知每个奶牛到每个挤奶机的路径，一个奶牛只能去一台机器，每台机器每天可以处理M头牛，求需要走最大距离去挤奶的牛的路径的最小值，用网络流＋二分答案，先假设最远的距离是求floyd时所求得的最短路径中的最大值，把源点和每头牛之间连容量为1的一条边，把每个挤奶器与汇点连容量为M的一条边，每头牛到挤奶机的距离如果小于或者等于dismax说明可以连接一条容量为1的边，然后求最大流，如果最大流等于C即牛的数量的时候，二分答案，直到求出答案为止。

2112

Accepted

5528K

750MS

G++

2883B

 #include <stdio.h>
 #include <string.h>
 #include <stdlib.h>
 #include <iostream>
 #include <algorithm>
 #include <queue>
 #include <stack>
 #define N 1000
 #define INF 999999999
 using namespace std;
 int mmap[N][N];
 int n;
 int k,c,m;
 int map[N][N];
 int pre[N];
 int maxn;
 int dismaxn;
 void floyd()
 {

     maxn=-;
     //for(int i=k+1;i<=n;i++)
        // for(int j=1;j<=k;j++)
             //cout<<"i:"<<i<<" j:"<<j<<" mmap[i][j]:"<<mmap[i][j]<<endl;
     for(int k=;k<=n;k++)
     {
         for(int i=;i<=n;i++)
         {
             for(int j=;j<=n;j++)
             {
                 mmap[i][j]=min(mmap[i][j],mmap[i][k]+mmap[k][j]);//保留原图

             }
         }
     }
     for(int i=k+;i<=n;i++)
         for(int j=;j<=k;j++)
             maxn=max(maxn,mmap[i][j]);//二分答案的上界

     dismaxn=maxn;
 }
 void build(int dismax)
 {
     memset(map,,sizeof(map));

     for(int i=k+;i<=n;i++)
     {
         for(int j=;j<=k;j++)
         {

             if(mmap[i][j]<=dismax)
             {
                 map[i][j]=;//建边

             }
         }
     }
     for(int i=k+;i<=n;i++)
     {
         map[][i]=;

     }
     for(int i=;i<=k;i++)
     {
         map[i][n+]=m;

     }
 }
 bool bfs(int s,int t)//寻找增广路径
 {
     int p;
     queue<int> q;
     memset(pre,-,sizeof(pre));
     pre[s]=s;
     q.push(s);
     while(!q.empty())
     {
         p=q.front();
         q.pop();
         for(int i=;i<=n+;i++)
         {

             if(map[p][i]>&&pre[i]==-)
             {
                 pre[i]=p;
                     if(i==t)
                     return true;
                 q.push(i);
             }
         }
     }
     return false;
 }
 bool ek(int s,int t)
 {
     int flow=,d,i;

     while(bfs(s,t))
     {
         d=INF;
         for(i=t;i!=s;i=pre[i])
             d=min(d,map[pre[i]][i]);
         for(i=t;i!=s;i=pre[i])
         {
             map[pre[i]][i]-=d;
             map[i][pre[i]]+=d;
         }
         flow+=d;
     }
     if(flow==c)
         return true;
     return false;
 }
 void bound()
 {
     int ub=maxn;
     int lb=;
     while(ub-lb>)
     {
         int mid=(lb+ub)/;
         build(mid);
         if(ek(,n+))
         {
             ub=mid;
         }
         else lb=mid;
     }
     printf("%d\n",ub);
 }
 int main()
 {
     while(scanf("%d %d %d",&k,&c,&m)!=EOF)
     {
         n=k+c;
         for(int i=;i<=n;i++)
         {
             for(int j=;j<=n;j++)
             {
                 scanf("%d",&mmap[i][j]);
                 if(mmap[i][j]==)
                     mmap[i][j]=INF;
             }
         }

         floyd();
         bound();
     }
 return ;
  }

4->POJ 1149

题意：有M个锁着的猪圈，每个猪圈有对应的猪的数量，每个猪圈能容纳无穷多的猪，Mirko没有猪圈的钥匙，顾客一个接着一个去农场买猪，每个顾客都有相应猪圈的钥匙和想买猪的数量，每次顾客打开猪圈之后，打开的猪圈里面的猪可以去任意打开的猪圈，要求出来每天能卖的最多的猪

思路：这题的建图有点麻烦，先按照样例建一个图

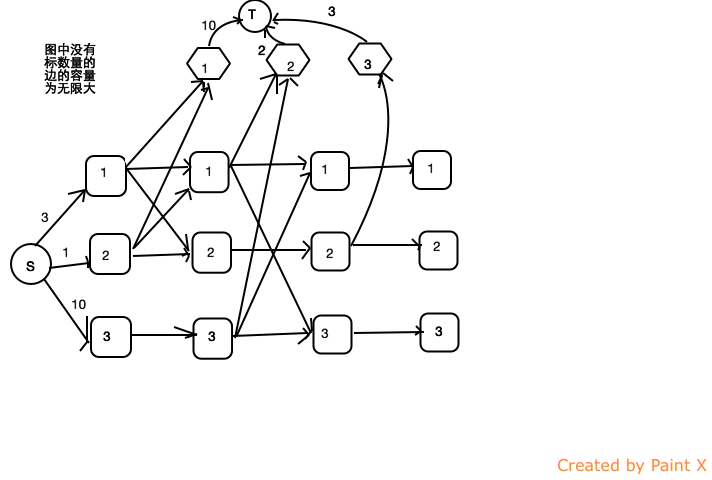
就算知道这题是求最大流的题目但是拿着这个图也写不了吧。。。

但是图是可以简化的

点的合并有这些规律

规律 1. 如果几个节点的流量的来源完全相同，则可以合并成一个

规律 2. 如果几个节点的流量的去向完全相同, 则可以把它们合并成一个。

规律 3. 如果从点 u 到点 v 有一条容量为 +∞ 的边,并且 u 是 v 的唯一流量来源,或者 v 是 u 的唯一流量去向,则可以把 u 和 v 合并成一个 节点。

简化完之后的图

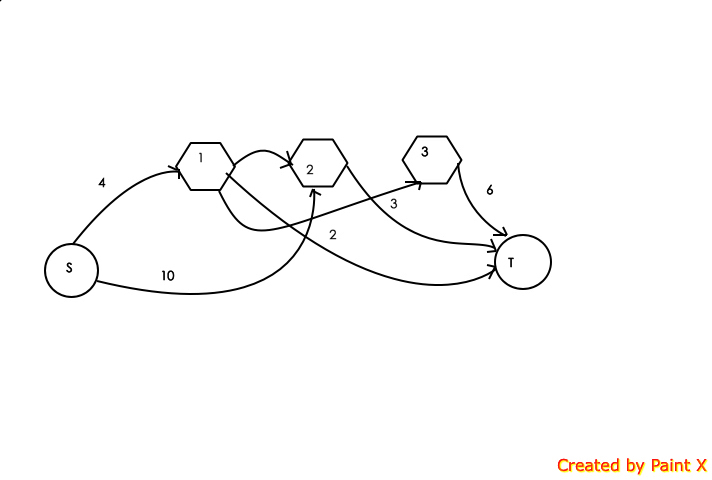
其实可以这么想这个图，每个猪圈的第一个顾客，就把这个猪圈就把源点向顾客连一条边，边的容量就是猪圈里面猪的数量，因为他是猪圈的第一个顾客，所以初始猪圈里面的猪他都能买，他打开了猪圈M之后，可能他打开的猪圈里面所有的猪都置换进了M里面，而M里面的猪可能又会被M的下一位顾客买走，所以对每个猪圈里面的1－n个用户，把i－>i+1连一条容量为无穷大的边

所以每次如果想不到什么好的构图方法的话，可以先根据样例把图画出来，然后利用简化的规则，把图简化一下，说不定就有建图的思路了。

1149

Accepted

1388K

47MS

G++

2198B

 #include <stdio.h>
 #include <string.h>
 #include <stdlib.h>
 #include <iostream>
 #include <algorithm>
 #include <queue>
 #include <vector>
 #include <stack>
 #define N 200
 #define INF 999999999
 using namespace std;
 int n,m;
 struct node
 {
     int key[];
     int cnt;
     int need;
 };
 node peo[N];
 int pre[N*N];
 int map[N][N];
 int pig[N*];
 bool vis[N*];
 vector<int> user[N*];
 void build()//建图
 {
     for(int i=;i<=m;i++)
     {
         for(int j=;j<user[i].size()-;j++)
         {
             map[user[i][j]][user[i][j+]]=INF;
         }
     }

 }
 bool bfs(int s,int t)
 {
     memset(pre,-,sizeof(pre));
    /* for(int i=0;i<=n+1;i++)
         for(int j=0;j<=n+1;j++)
             cout<<"i:"<<i<<"j:"<<j<<"map[i][j] "<<map[i][j]<<endl;*/
     queue<int> q;
     q.push(s);
     pre[s]=s;
     while(!q.empty())
     {
         int p=q.front();
         q.pop();
         for(int i=;i<=n+;i++)
         {
             if(map[p][i]>&&pre[i]==-)
             {
                 pre[i]=p;
                 if(i==t)
                     return true;
                 q.push(i);
             }

         }
     }
     return false;
 }
 int EK(int s,int t)
 {
     int d,flow=;
     while(bfs(s,t))
     {
         d=INF;
         for(int i=t;i!=s;i=pre[i])
             d=min(d,map[pre[i]][i]);
         for(int i=t;i!=s;i=pre[i])
         {
             map[pre[i]][i]-=d;
             map[i][pre[i]]+=d;

         }
         flow+=d;
     }
     return flow;
 }
 int main()
 {
     while(scanf("%d %d",&m,&n)!=EOF)
     {
         for(int i=;i<=m;i++)
             scanf("%d",&pig[i]);
         memset(vis,false,sizeof(vis));
         for(int i=;i<=n;i++)
         {
             scanf("%d",&peo[i].cnt);
             for(int j=;j<=peo[i].cnt;j++)
             {
                 scanf("%d",&peo[i].key[j]);
                 user[peo[i].key[j]].push_back(i);//每个猪圈按照顺序把顾客编号放进去
                 if(!vis[peo[i].key[j]])//给第一个顾客连线
                 {
                     map[][i]+=pig[peo[i].key[j]];
                     vis[peo[i].key[j]]=true;
                 }
             }
             scanf("%d",&peo[i].need);
             map[i][n+]=peo[i].need;//顾客和汇点连线
         }
         build();//建图
         printf("%d\n",EK(,n+));
     }
     return ;
 }