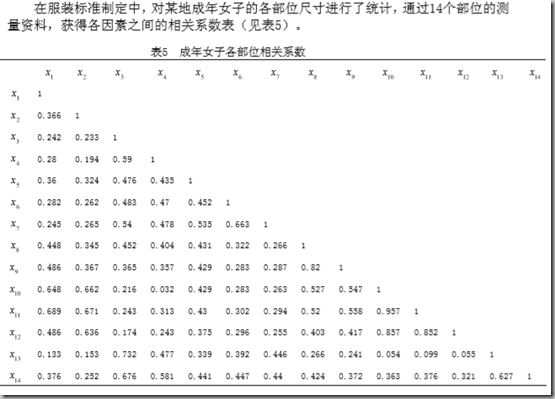
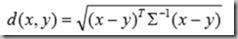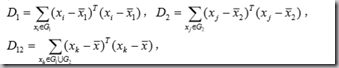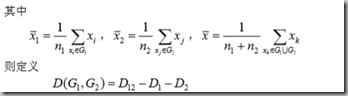【数学建模】day09-聚类分析

0.

多元分析之聚类分析。

聚类分析是一种定量方法，从数据的角度，对样本或指标进行分类，进而进行更好的分析。

分为Q型聚类和R型聚类。

1.

Q型聚类分析是对样本进行分类。有若干样本，我们把这些样本分成几类，每一类中的样本之间是“相似”的。

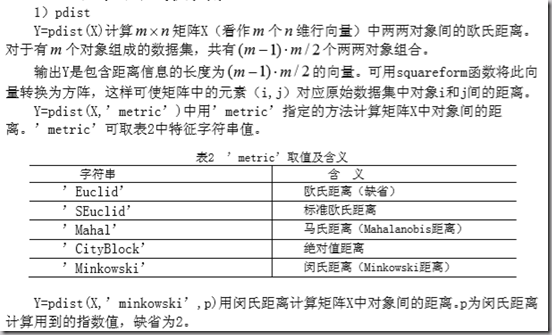
1）样本的相似性度量

样本之间的距离来描述样本之间的相似性。

常用的有绝对值距离、欧氏距离。使用欧氏距离必须标准化处理，但避免不了变量的多重相关性。

解决：使用马氏距离（ Mahalanobis）。

式子中，x、y是来自总体Z两个样本（向量）。∑是Z的协方差矩阵。

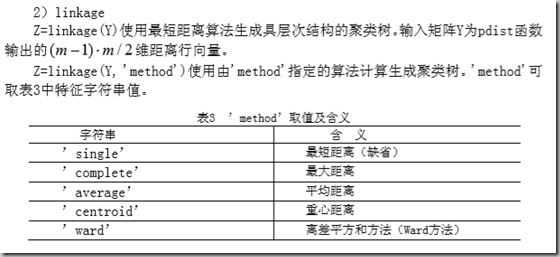
2）类与类之间的相似性度量

如何衡量两个类之间的相似度。

常用的有：

最短距离法：两类中最近两点之间的距离。

最长距离法：两类中最远两点之间的距离。

重心法：两类数据重心的距离。

类平均法：两类所有两两点之间距离的平均。

离差平方和法：

3）Q型聚类分析以及实现

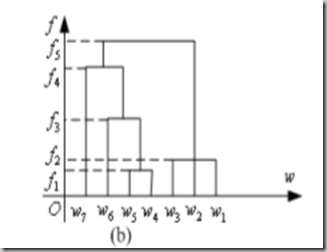
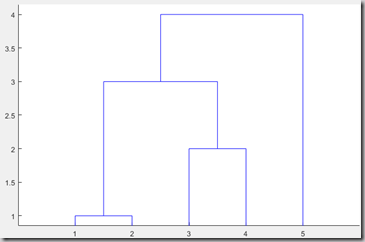
假设有w1,w2,w3…w7这些样本点，Q型聚类就是完成下图：

图中，f坐标代表“平台高度”，实际上是距离值。相同平台高度下各自分为两类。

如若分成3类，则在f3高度下，分为{w7},{w6,w5,w4},{w3,w2,w1}三类。

Q型聚类步骤：

• 1 ）计算n个样本点两两之间的距离dij ，记为矩阵D = （dij）（n*n）；
• 2）首先构造n个类，每一个类中只包含一个样本点，每一类的平台高度均为零
• 3）合并距离近的两类为新类，并且以这两类间的距离值作为聚类图中的平台高 度；
• 4）计算新类与当前各类的距离，若类的个数已经等于 1，转入步骤 5），否则，回 到步骤 3）；
• 5）画聚类图；
• 6）决定类的个数和类。

4） MATLAB实现Q型聚类分析

相关MATLAB函数如下，需要查询下面。

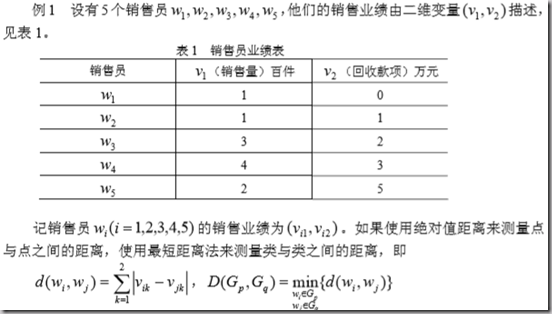
5）一个使用例子：

解决：

 clc,clear
  a = [,;,;,;,;,];
  y = pdist(a,'cityblock') %计算绝对值距离
 yc = squareform(y);
  z = linkage(y) %最短距离法产生聚类树

 [h,t] = dendrogram(z) %画聚类图命令
 T = cluster(z,'maxclust',) %把对象划分为3类
 for i = :
      tm = find(T == i);%返回第i类对象
      tm = reshape(tm,,length(tm));%编程行向量
      fprintf('第%d类对象有%s\n',i,int2str(tm));
  end

聚类图如下：

产生聚类树的z = linkage(y)得到：

这是一个(m-1)*3的矩阵，m是样例数。

1和2连接，平台高度是1；1和2连接后，新样例做第6点（m+j）。

3和4连接，平台高度是2；做第7点。

6和7连接，平台高度3；做第8点。

5和8连接。

若分成三类，打印结果如下：

3.

R型聚类。

R型聚类是更常用的。影响指标有若干，但这些影响因素（自变量）之间可能有相关性，把比较相关的聚成一类，只选用其中的一个因素来代表该类，从而对问题做出简化。

Q与R的对比：

Q是对样本进行聚类，通过样本之间的距离，结果是把各个样本分堆。

R是要最自变量进行聚类，通过自变量之间的相关系数（这个计算是根据样本计算的），进而对自变量之间的相关性做出分析，相关性大的自变量分在一类，结果是把自变量分堆。

1） 样本之间的距离

采用取Q型相同的方法。

2） 两类之间的距离

r为相关系数。这些操作都是基于相关系数的。

3）具体例子：

计算如下：

 clc,clear
  a = textread('ch.txt')
  d =  - abs(a); %相关系数转距离
 d = tril(d); %提出d矩阵的下三角部分
 b = nonzeros(d);%去掉d的0
  b = b';
  z = linkage(b,'complete') %最大距离,产生聚类树
 y = cluster(z,'maxclust',) %变量分为2类
 ind1 = find(y == );
  ind1 = ind1'
  ind2 = find(y == );
  ind2 = ind2'
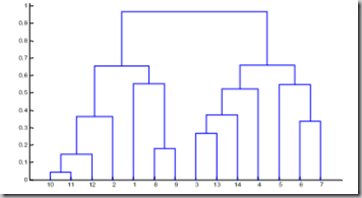
  dendrogram(z) %画聚类图

产生聚类图如下：

通过聚类图，可以看出，人体的变量大体可以分为两类：

一类反映人高、矮的变量， 如上体长，手臂长，前腰节高，后腰节高，总体长，身高，下体长；

另一类是反映人体 胖瘦的变量，如胸围，颈围，总肩围，总胸宽，后背宽，腰围，臀围。