基于MMSE的预测

本文的目的是预测随机变量的输出值。

既然有预测值，那么我们就需要一个判断基准（criterion）用于判断该预测值与该随机变量的实际输出之间的差值，这里采用的判断基准就是MSE（mean-square-error）。MSE越小，则表明预测值越接近随机变量的实际输出值，因此在求一个随机变量的预测值时，该预测值与随机变量之间应该有MMSE（minimum mean-square-error）。

$\displaystyle{ MSE = E[(X-\hat{x})^2] = \frac{1}{N}\sum_{n=1}^{N}(x_n-\hat{x})^2}$

其中$X$就是随机变量，$x_n$是随机变量的实验输出值，$\hat{x}$是该随机变量的预测值。

预测一个连续随机变量

我们知道一个连续随机变量$Y$的PDF为$f_Y(y)$，现在我们希望预测该随机变量的值，假设预测值为$\hat{y}$，那么有MSE如下

$MSE = \displaystyle{E[(Y-\hat{y})^2] = \int(y-\hat{y})^2f_Y(y)dy}$

我们需要求得一个值$\hat{y}$，使得这个式子得到一个最小值MMSE。因此把$\hat{y}$当作自变量，并对该式子求导，当导数为0时能得到一个极值

$\displaystyle{-2\int(y-\hat{y})f_Y(y)dy =0}$

对上述式子进行整理得到

$\displaystyle{ \int\hat{y}f_Y(y)dy = \int yf_Y(y)dy } = E[Y]$

因此有

$\color{red}{\hat{y} = E[Y]}$

此外，MSE的二阶导为

$\displaystyle{2\int f_Y(y)dy = 2}$

即一阶导数的斜率固定为2，这表明MSE曲线只有一个极值，并且是一个极小值（MSE曲线开口向上）。因此对随机变量进行MMSE预测得到的预测值为$\hat{y} = E[Y]$。而实际的MMSE就是方差$MMSE = \sigma_Y^2$。

预测条件连续随机变量

两个随机变量

对于具有两个随机变量的联合概率分布$f_{X,Y}(x,y)$，在已知$X=x$的情况下，$Y$的PDF为$f_{Y|X}(y|x)$。

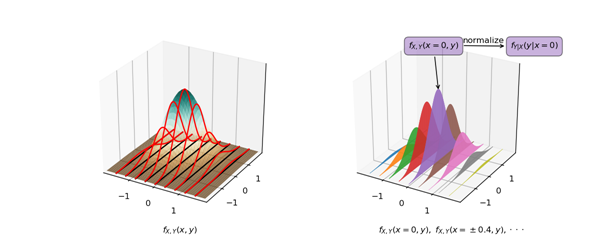
通过上图能方便理解，当固定某个随机变量$X=x_0$时，通过联合PDF能知道随机变量$Y$的概率分布$f_{X,Y}(x_0,y)$，不过此时不一定有$\displaystyle{\int_{-\infty}^{\infty}f_{X,Y}(x_0,y)dy=1}$，因此需要对其进行标准化后才能得到$f_{Y|X}(y|x=x_0)$。

通过选定不同的$x$，会有不同的$f_{Y|X}(y|x)$，因此期望值$E[Y|X=x]$也会有所不同。结合上一小节可以知道，当$X=x$时，选择$E[Y|X=x]$作为预测值可以使得MSE最小。

$\displaystyle{ E[\{Y-\hat{y}(x)\}^2|X=x]=\int\{y-\hat{y}(x)\}^2f_{Y|X}(y|x)dy }$

其中$\hat{y}(x)$是当$X=x$时，随机变量Y的预测值

$\color{red}{\hat{y}(x) = E[Y|X=x] = \displaystyle{\int_{-\infty}^{\infty}yf_{Y|X}(y|x)dy}}$

这就是当$X=x$时，对随机变量$Y$的进行MMSE预测所得到的预测结果。

同样，MMSE的值就是$f_{Y|X}(y|x)$的方差$\sigma_{Y|X}^2$，即

$MMSE =\sigma_{Y|X}^2$

多个随机变量

推广到多个随机变量联合分布有：当$X_1=x_1,X_2=x_2,\cdot\cdot\cdot,X_L=x_L$时，随机变量$Y$的PDF为

$f_{Y|X_1,X_2,\cdot\cdot\cdot,X_L}(y|x_1,x_2,\cdot\cdot\cdot,x_L)$

此时对随机变量$Y$进行MMSE预测，预测值为

$\hat{y}(x_1,x_2,\cdot\cdot\cdot,x_L) = E[Y|X_1=x_1,X_2=x_2,\cdot\cdot\cdot,X_L=x_L]$

为了方便，我们把$X_1=x_1,X_2=x_2,\cdot,\cdot,\cdot,X_L=x_L$记为具有$L$个元素的向量$\textbf{X}$，因此上面的式子可以写为

$\displaystyle{ \hat{y}(\textbf{x}) = \int_{-\infty}^{\infty}yf_{Y|\textbf{X}}(y|\textbf{X}=\textbf{x})dy = E[Y|\textbf{X} = \textbf{x}] }$

Estimator（预测器）

在前一小节中，我们知道当有前置条件$X=x$时，随机变量$Y$的预测值为$\hat{y}(x) = E[Y|X=x]$，该预测值是与$x$相关的。这里我们可以把$\hat{y}(x)$当作是一个函数，其输入值为$x$。有了输入值$x$，我们可以去预测输出值$\hat{y}(x)$，因此我们也能将$\hat{y}()$当成一个预测器。

输入值为随机变量

前面的小节讨论的都是当$X=x$时的预测值，预测器的输入为一个固定值，因此预测器输出的也是一个值$\hat{y}(x)$。如果我们用随机变量$X$作为输入，那么有

$\hat{Y} = \hat{y}(X) = E[Y|X]$

输出值$\hat{Y}$也是一个随机变量，该随机变量的每一个可能的输出值都从随机变量$X$的可能输出值映射得来，因此可以认为他们共享同一个PDF$f_X(x)$。

由于预测值$\hat{Y}$是一个随机变量，因此如果按照前面的方法计算，MMSE也会是一个随机变量，所以此时MMSE的值应该按照如下方式计算

$\color{red}{\begin{align*}E_{Y,X}\Big( [Y-\hat{y}(X)]^2 \Big)
&=E_X\bigg(E_{Y|X}\Big( [Y-\hat{y}(X)]^2|X \Big) \bigg)\\
&=\int_{-\infty}^{\infty}E_{Y|X}\Big( [Y-\hat{y}(x)]^2|X=x \Big)f_X(x)dx
\end{align*}}$

正交性

在学习概率模型的向量空间时说过，如果两个向量的内积为0，则认为它们正交。实际上$Y-\hat{y}(X)$与任意关于随机变量$X$的函数$h(X)$是正交的

$\color{red}{E_{Y,X}[\{Y-\hat{y}(X)\}h(X)] = 0}$

证明：

$\begin{align*}
E_{Y,X}[\hat{y}(X)h(X)] &= E_{X,Y}[E_{Y|X}[Y|X]h(X)]\\
&=E_{X}[E_{Y|X}[Y|X]h(X)]\\
&=E_{X}[E_{Y|X}[Yh(X)|X]]\\
&=E_{Y,X}[Yh(X)] \qquad \href{http://www.cnblogs.com/TaigaCon/p/8887931.html#DualVarBayesRule}{Bayes'\ Rule}\end{align*}$

因此

$\begin{align*}&\quad\ E_{Y,X}[\hat{y}(X)h(X)]-E_{Y,X}[Yh(X)]\\ &= E_{Y,X}[\{Y-\hat{y}(X)\}h(X)]\\ &= 0\end{align*}$

 

线性预测

我们前面讨论的预测器$\hat{y}(X)$是基于随机变量$X$来预测随机变量$Y$，理想的预测器是$\hat{y}(x) = E[Y|X=x] = \displaystyle{\int_{-\infty}^{\infty}yf_{Y|X}(y|x)dy}$。这个预测器固然是最佳的MMSE预测器，不过它依赖于条件PDF $f_{Y|X}(y|x)$，而这个条件PDF通常比较难以获取，因此我们在这里提出一个简单实用的预测器Linear MMSE Estimator。

LMMSE预测器假设条件（随机变量$X$）与结果（随机变量$Y$）之间具有线性关系，即

$\hat{Y}_{\ell} = \hat{y}_{\ell}(X) = aX+b$

求系数$a,b$的值

预测是基于MMSE，因此有

$MSE = E_{Y,X}[(Y-\hat{Y}_{\ell})^2] = E_{Y,X}[\{Y-(aX+b)\}^2]$

其中系数$a,b$是所要求的未知值，我们需要选取合适的$a$以及$b$以使得MSE最小。首先求系数$b$，对MSE求变量$b$的导数，

$\begin{align*}\frac{dMSE}{db} &= \frac{dE_{Y,X}[\{Y-(aX+b)\}^2]}{db}\\
&=\frac{dE_{Y,X}[Y^2+a^2X^2+b^2-2aYX-2Yb+2aXb]}{db}\\
&=2E_{Y,X}[Y-(aX+b)]
\end{align*}$

对于变量$b$，MSE是一个开口向上的二次函数，当该二次函数的一阶导为0时有最小值，即有MMSE

$\begin{align*}
E_{Y,X}[Y-(aX+b)] &= E_{Y,X}[Y]-E_{Y,X}[aX]-b\\
&=E[Y]-aE[X]-b\\
&=\mu_y-a\mu_x-b\\
&= 0
\end{align*}$

此时$b$的值为

$\color{red}{b = \mu_y-a\mu_x}$

接下来求系数$a$的值。同样是从MSE的式子开始，

$\begin{align*}
MSE &= E_{Y,X}[(Y-\hat{Y}_{\ell})^2]\\
&= E_{Y,X}[\{(Y-\mu_y)-(\hat{Y}-\mu_y)\}^2]\\
&= E_{Y,X}[\{(Y-\mu_y)-(aX+b-\mu_y)\}^2]\\
&= E_{Y,X}[\{(Y-\mu_y)-(aX-a\mu_x+\mu_y-\mu_y)\}^2]\\
&= E_{Y,X}[\{(Y-\mu_y)-a(X-\mu_x)\}^2]\\
&= E_{Y,X}[(\tilde{Y}-a\tilde{X})^2]\qquad letting \left\{\begin{matrix}\tilde{Y}=Y-\mu_y\\ \tilde{X}=X-\mu_x\end{matrix}\right.
\end{align*}$

然后对MSE进行变量为$a$的求导，

$\begin{align*}
\frac{dMSE}{da} &= \frac{dE_{Y,X}[(\tilde{Y}-a\tilde{X})^2]}{da}\\
&= \frac{dE_{Y,X}[\tilde{Y}^2+a^2\tilde{X}^2-2a\tilde{Y}\tilde{X}]}{da}\\
&= E_{Y,X}[2a\tilde{X}^2-2\tilde{Y}\tilde{X}]\\
&= 2aE_{Y,X}[\tilde{X}^2]-2E_{Y,X}[\tilde{Y}\tilde{X}]\\
&= 2a\sigma_X^2-2\sigma_{Y,X}\\
&= 2a\sigma_X^2-2\rho\sigma_X\sigma_Y\qquad \href{http://www.cnblogs.com/TaigaCon/p/8887931.html#UsefulVectorSpace}{\sigma_{Y,X}=\rho\sigma_X\sigma_Y}
\end{align*}$

当导数为0时有最小的MSE，

$2a\sigma_X^2-2\rho\sigma_X\sigma_Y=0$

那么此时的系数$a$为

$\color{red}{a = \rho\frac{\sigma_Y}{\sigma_X}}$

因此LMMSE预测器为

$\color{red}{\hat{Y}_{\ell} = aX+b = \rho\frac{\sigma_Y}{\sigma_X}(X-\mu_X)+\mu_Y}$

线性预测器的向量空间

回顾前面对MSE进行变量为$a$的求导，把求导的式子进行整理

$\begin{align*}
\frac{dMSE}{da} &= \frac{dE_{Y,X}[(\tilde{Y}-a\tilde{X})^2]}{da}\\
&= \frac{dE_{Y,X}[\tilde{Y}^2+a^2\tilde{X}^2-2a\tilde{Y}\tilde{X}]}{da}\\
&= E_{Y,X}[2a\tilde{X}^2-2\tilde{Y}\tilde{X}]\\
&= 2E_{Y,X}[(a\tilde{X}-\tilde{Y})\tilde{X}]\\
&= -2E_{Y,X}[(\tilde{Y}-a\tilde{X})\tilde{X}]
\end{align*}$

由前一小节已知系数$a$能使得该导数式子的结果为0，

$E[(\tilde{Y}-a\tilde{X})\tilde{X}] = 0$

在此引入向量空间，该向量空间中的向量有以下几个特征：

1. 向量$\tilde{Y}-a\tilde{X}$与向量$\tilde{X}$正交
2. 向量$\tilde{Y}-a\tilde{X}$与向量$a\tilde{X}$之和为$\tilde{Y}$
3. 向量$\tilde{Y}-a\tilde{X} = Y-\mu_Y-a(X-\mu_X) = Y-\hat{Y}_{\ell}$
4. 向量$\tilde{Y}$与向量$\tilde{X}$之间的夹角为$\theta$，$\rho$是随机变量$X$与$Y$的相关系数，有$\rho = cos(\theta)$

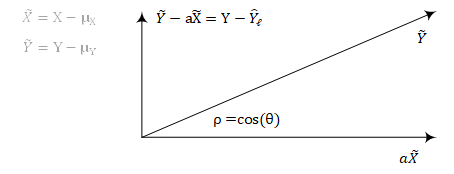
LMMSE预测器的MMSE为

$\begin{align*}
MMSE &= E_{Y,X}[(Y-\hat{Y}_{\ell})^2]\\
&= E_{Y,X}[(\tilde{Y}-a\tilde{X})^2]\\
&= E[\tilde{Y}^2]-E[(a\tilde{X})^2]\qquad (\tilde{Y}-a\tilde{X})\ orthogonal\ to\ (a\tilde{X}) \\
&= E[\tilde{Y}^2]-\rho^2E[\tilde{Y}^2]\\
&= \sigma_Y^2(1-\rho^2)
\end{align*}$

这个MMSE的结果表明

1. 如果随机变量$X$与$Y$之间真的具有线性关系的话，即$\rho=1$，那么就能得到$MMSE=0$
2. 如果随机变量$X$与$Y$相互独立的话，即$\rho=0$，那么$MMSE = \sigma_Y^2$
3. 随机变量$X$与$Y$之间的相关性越强，即$\rho$越大的话，就能得到越小的MMSE，而MMSE越小，则可以认为预测的数值越准确

这种线性预测器也能推广到多随机变量，即预测器假设一个随机变量$Y$与多个随机变量$\textbf{X}=[X_1, X_2,\cdot\cdot\cdot,X_L]$具有线性关系。有兴趣可以自行查阅下面Reference的链接。

Reference：

Alan V. Oppenheim: Signals, Systems and Inference, Chapter 8: Estimation with Minimum Mean Square Error