最大矩阵（简单DP）

见题：

很水的一题，数据范围太小，前缀和加爆搜就行.

#include<bits/stdc++.h>
using namespace std;
const int maxn=;
int ans=,m,n,sum[maxn][maxn];
inline int read()
{
    int x=,ff=;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-') ff=-;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return x*ff;
}
inline void put(int x)
{
    if(x<) putchar('-'),x=-x;
    if(x>) put(x/);
    putchar(x%+'');
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=m;j++)
        {
            int x=read();
            sum[i][j]=sum[i-][j]+sum[i][j-]-sum[i-][j-]+x;
        }
    }
    for(int len=;len<=min(n,m);len++)
    {
        int he=len*len;
        for(int x1=;x1<=n-len+;x1++)
        {
            for(int y1=;y1<=m-len+;y1++)
            {
                int x2=x1+len-;
                int y2=y1+len-;
                if((sum[x2][y2]-sum[x1-][y2]-sum[x2][y1-]+sum[x1-][y1-])==he) ans=len;
            }
        }
    }
    put(ans);
    return ;
}

可是还是想写正解，DP；

对于这类的二维DP，个人理解就是如果保存的从起点到终点的状态会被一些情况所中断，就要只考虑最下角的点所保存的点的状态，例如此题，我们可以保存以（i,j）为右下角的状态，以f[i][j]保存以(i,j)为最右下角的最大正方形边长.状态转移怎么样呢？

这是我们我们可以轻易的想起二维的前缀和：f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+a[i][j],那这个能否用前缀和处理呢，见下图：

最右下的小矩阵代表（i，j）可以很清楚地看出由左边的点，上边的点，左上角的点三个点的最小矩阵构成以个完整的矩阵，即：if(a[i][j]==1) f[i][j]=min(f[i-1][j-1],min(f[i-1][j],f[i][j-1]))+1;

这也提醒我们min的意义就是几个状态都具备的共同元素.

#include<bits/stdc++.h>
using namespace std;
const int maxn=;
int m,n,a[maxn][maxn],f[maxn][maxn],ans;
inline int read()
{
    int x=,ff=;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-') ff=-;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return x*ff;
}
int put(int x)
{
    if(x<) putchar('-'),x=-x;
    if(x>) put(x/);
    putchar(x%+'');
}
inline void DP()
{
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=m;j++)
        {
            if(a[i][j]==) f[i][j]=min(f[i-][j-],min(f[i-][j],f[i][j-]))+;
            ans=max(ans,f[i][j]);
        }
    }
}
int main()
{
    freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=m;j++) a[i][j]=read();
    }
    DP();
    put(ans);
    return ;
} 

下一题：

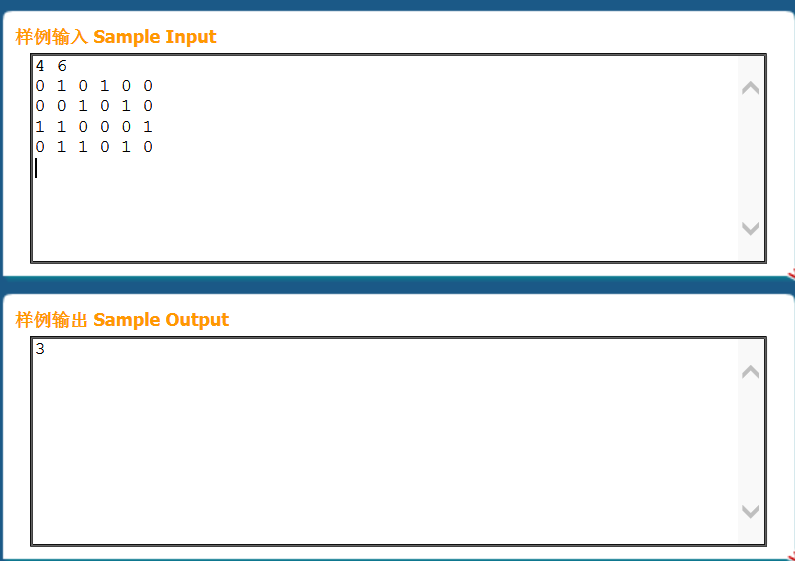
这一题就不能用暴力了，（n<=2600,m<=2600）只能想正解，和上一题一样我们可以用f[i][j]一（i，j）保存合法的吃到的最大的鱼的个数.

接下来就考虑状态怎么转移，我自己也是嗑了许多时间还没做出来，于是就看了题解...

给出代码：

#include<bits/stdc++.h>
using namespace std;
#define _ 0
const int maxn=;
int m,n,a[maxn][maxn],f[maxn][maxn],s1[maxn][maxn],s2[maxn][maxn],ans;
inline int read()
{
    int x=,ff=;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-') ff=-;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return x*ff;
}
inline void put(int x)
{
    if(x<) putchar('-'),x=-x;
    if(x>) put(x/);
    putchar(x%+'');
}
int main()
{
    freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=m;j++) a[i][j]=read();
    }
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=m;j++)
        {
            if(!a[i][j])
            {
                s1[i][j]=s1[i][j-]+;
                s2[i][j]=s2[i-][j]+;
            }
            if(a[i][j])
            {
                f[i][j]=min(f[i-][j-],min(s1[i][j-],s2[i-][j]))+;
                ans=max(ans,f[i][j]);
            }
        }
    }
    memset(f,,sizeof(f));
    memset(s1,,sizeof(s1));
    memset(s2,,sizeof(s2));
    for(int i=;i<=n;i++)
    {
        for(int j=m;j>=;j--)
        {
            if(!a[i][j])
            {
                s1[i][j]=s1[i][j+]+;
                s2[i][j]=s2[i-][j]+;
            }
            if(a[i][j])
            {
                f[i][j]=min(f[i-][j+],min(s1[i][j+],s2[i-][j]))+;
                ans=max(ans,f[i][j]);
            }
        }
    }
    put(ans);
    return (^_^);
}

启示我们可以直接从最优解的转移推状态转移方程...