KNN-笔记(1)

1 - 背景

KNN：k近邻，表示基于k个最近的邻居的一种机器学习方法。该方法原理简单，构造方便。且是一个非参数化模型。

KNN是一个“懒学习”方法，也就是其本身没有训练过程。只有在对测试集进行结果预测的时候才会产生计算。KNN在训练阶段，只是简单的将训练集放入内存而已。该模型可以看成是对当前的特征空间进行一个划分。当对测试集进行结果预测时，先找到与该测试样本最接近的K个训练集样本，然后基于当前是分类任务还是回归任务来做对应的处理。

KNN模型中有三个需要注意的地方：

1 - 距离度量的方法；

2 - K值的选择；

3 - 最后的判别决策规则。

如上面第三个，较为简单的判别决策规则为：

1）分类任务，那么找这K个训练集样本中出现次数最多的那个标签作为该测试样本标签，如下图：



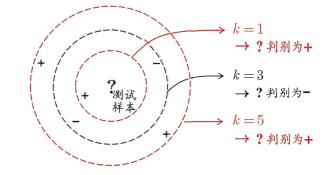
图1.1 周老师西瓜书图10.1

2）回归任务，基于这K个训练集样本求均值，将其作为该测试集样本的结果。

不过KNN正是因为基于K个近邻进行测量的方法，所以其出问题也就在这里，因为该模型不适合作为高特征维度下的选择。因为它会遇到维数灾难的问题。举个例子，假如当前数据集是均匀分布在一个D维特征的空间中的，假设我们需要计算测试样本\(x\)周边一个区域上的类别标签密度，那么我们期望基于足够大的区域范围的数据才能得到合理的结果，那么对应的边界长度公式为：

\[e_D(f) = f^{1/D}
\]

也就是假如维度为\(D=10\)，我们想评估10%的类别标签密度，那么每个维度上所需长度为\(e_{10}(0.1) = 0.8\)，也就是我们需要每个维度上80%的长度范围内的数据，即使我们只需要估计1%的标签密度，我们每个维度上的长度也是\(e_{10}(0.01)=0.63\) 。



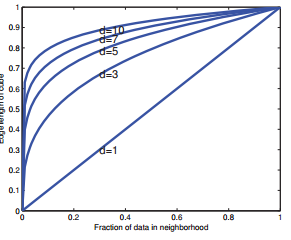
图2.2 mlapp上图1.16（b）

当维度为2，且样本能够无限多，那么该模型表现才是最好的(Cover and Hart 1967)。所以按道理，高维数据其实不适合KNN[]

不过幸运的是， 有一个效应可以在一定程度上抵消维度灾难， 那就是所谓的“ 非均匀性的祝福”（blessing of nonuniformity） 。
在大多数应用中， 样例在空间中并非均匀分布， 而是集中在一个低维流形manifold） 上面或附近。
这是因为数字图片的空间要远小于整个可能的空间。 学习器可以隐式地充分利用这个有效的更低维空间， 也可以显式地进行降维。[]

2 距离度量

KNN中最常用的方法就是欧式距离计算法，当然也有\(L_p\)距离和马氏距离等等。

假设样本的特征空间\(\chi\)是\(n\)维实数的向量空间\(\bf R^n\)，\(x_i,x_j\in\chi\),$x_i=(x_i^{(1)}, x_i^{(2)}, ..., x_i^{(n)} ) \(,\)x_j=(x_j^{(1)},x_j{(2)},...,x_j^{(n)})\(,那么\)x_i,x_j\(的\)L_p$距离定义为：

\[L_p^{(x_i,x_j)}=(\sum_{l=1}^n|x_i^{l}-x_j^{l}|^p)^{\frac{1}{p}}
\]

这里\(p\geq1\),

当\(p=2\)时，称为欧式距离；

当\(p=1\)时，称为曼哈顿距离；

当\(p=\infty\)时，是各个坐标距离的最大值，即：

\[L_\infty(x_i,x_j)={max}_l|x_i^{(l)}-x_j^{(l)}|
\]

图2.1 李航统计学习方法图3.2

上图为在2维情况下到原点的距离为\(L_p=1\)的点构成的范围图

3 K值选取

K值的选择会对KNN模型的结果产生重大影响。这就是一个模型选择问题。

模型选择：假设当前是一个KNN回归问题。现在是需要对点\(x_0\)进行\(\hat f_k(x_0)\)拟合，假设该样本来自函数\(Y=f(X)+\epsilon\), 这里\(E(\epsilon)=0\), 且\(Var(\epsilon)=\sigma^2\)。为了简化问题，假设训练样本中\(x_i\)的值是固定的，那么在测试样本点\(x_0\)的期望预测误差也叫做测试或泛化误差，如：

\[\begin{eqnarray}
EPE_k^{(x_0)}
&=& E[(Y-\hat f_k(x_0))^2|X=x_0]\\
&=& \sigma^2+[Bias^2(\hat f_k(x_0))+Var(\hat f_k(x_0))]\\
&=& \sigma^2+[f(x_0)-\frac{1}{k}\sum_{l=1}^kf(x(l))]^2+\frac{\sigma^2}{k}
\end{eqnarray}\]

第一项叫做不可避免的误差，是我们不可控制的，第二项和第三项是我们能够控制的，分别对应着模型的偏置和方差。偏置随着K变大而变大，方差随着K变大而变小。即K越大，模型越简单，K越小，模型越复杂：



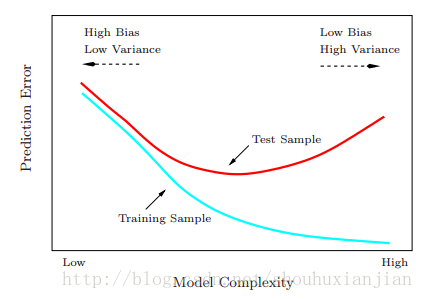
图2.2 esl书上的图2.11

4 搜索优化

实现KNN模型时，主要考虑的还有个问题是如何对训练集的样本点进行快速的K近邻搜索。当特征空间维度太大，或者训练集样本点很多的时候特别重要。最基础的搜索方法就是线性搜索了，可想而知每个测试样本在比较时，都需要去计算一遍训练集的所有样本。效率着实不高。所以才需要量身定做的数据结构搜索方法。

4.1 - KD树

见这里

4.2 - Ball树

(待续)

参考资料：

[] Machine Learning A Probabilistic Perspective

[] 李航，统计学习方法

[] The Elements of Statistical Learning Data Mining, Inference, and Prediction (Second Edition)

[] Pedro Domingos,A Few Useful Things to Know About Machine Learning

[] 以叶子为数据的http://www.cnblogs.com/lysuns/articles/4710712.html

[] http://blog.csdn.net/likika2012/article/details/39619687