[Unity Quaternion]四元数Quaternion的计算方式

什么是Quaternion四元数

1843年，William Rowan Hamilton发明了四元数，但直到1985年才有一个叫Ken Shoemake的人将四元数引入计算机图形学处理领域。四元数在3D图形学中主要用于旋转，骨骼动画等。

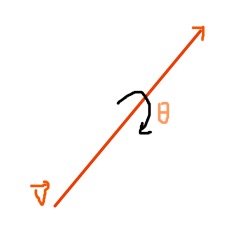
简单地来说，四元数描述了一次旋转：绕任意一个轴(V)旋转一个弧度(θ)。

那么四元数q就与(V,θ)两个参数有关。

具体公式:

q = (sin(θ / 2) * V,cos(θ / 2) )

q = (sin(θ / 2) * x,sin(θ / 2) * y,sin(θ / 2) * z,cos(θ / 2))

在Unity中使用Quaternion对象

创建Quaternion对象

//
float radians = 90 / 360f * Mathf.PI * 2;
//
Vector3 n = Vector3.up;

//
float w = Mathf.Cos (radians / 2);
//
float s = Mathf.Sin (radians / 2);

//
float x = n.x * s;
float y = n.y * s;
float z = n.z * s;

//
transform.rotation = new Quaternion (x, y, z, w);

上述代码，可以设置一个游戏对象沿着Y轴向上的方向顺时针旋转90度

Quaternion对象的方法

实例方法

Set用法

//
float radians = degress / 360f * Mathf.PI * 2;
//
Vector3 n = Vector3.up;

//
float w = Mathf.Cos (radians / 2);
//
float s = Mathf.Sin (radians / 2);

//
float x = n.x * s;
float y = n.y * s;
float z = n.z * s;

//
Quaternion q = new Quaternion ();
q.Set (x, y, z, w);

//
transform.rotation = q;

SetFromRatation用法

//
Quaternion q = new Quaternion ();
q.SetFromToRotation (Vector3.up, Vector3.left);

//
transform.rotation = q;

SetLookRotation用法

//
Quaternion q = new Quaternion ();
q.SetLookRotation (Vector3.back);

//
transform.rotation = q;

静态方法

//
transform.rotation = Quaternion.identity;

//
transform.rotation = Quaternion.AngleAxis (degress, Vector3.up);

//
transform.rotation = Quaternion.Dot (q1, q2);

//
transform.rotation = Quaternion.Inverse (q1);

//
transform.rotation = Quaternion.Lerp(q1,q2,Time.deltaTime);

//
transform.rotation = Quaternion.Slerp (q1, q2, Time.deltaTime);