PrefixSpan算法原理总结

　　　　前面我们讲到频繁项集挖掘的关联算法Apriori和FP Tree。这两个算法都是挖掘频繁项集的。而今天我们要介绍的PrefixSpan算法也是关联算法，但是它是挖掘频繁序列模式的，因此要解决的问题目标稍有不同。

1. 项集数据和序列数据

　　　　首先我们看看项集数据和序列数据有什么不同，如下图所示。

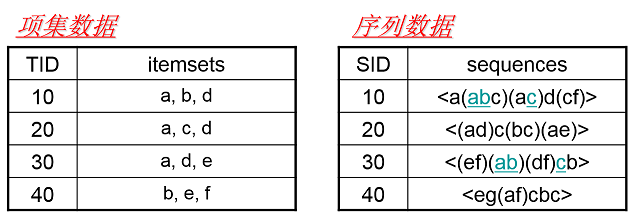
　　　　左边的数据集就是项集数据，在Apriori和FP Tree算法中我们也已经看到过了，每个项集数据由若干项组成，这些项没有时间上的先后关系。而右边的序列数据则不一样，它是由若干数据项集组成的序列。比如第一个序列<a(abc)(ac)d(cf)>,它由a,abc,ac,d,cf共5个项集数据组成，并且这些项有时间上的先后关系。对于多于一个项的项集我们要加上括号，以便和其他的项集分开。同时由于项集内部是不区分先后顺序的，为了方便数据处理，我们一般将序列数据内所有的项集内部按字母顺序排序。

2. 子序列与频繁序列

　　　　了解了序列数据的概念，我们再来看看上面是子序列。子序列和我们数学上的子集的概念很类似，也就是说，如果某个序列A所有的项集在序列B中的项集都可以找到，则A就是B的子序列。当然，如果用严格的数学描述，子序列是这样的：

　　　　对于序列A={$a_1,a_2,...a_n$}和序列B={$b_1,b_2,...b_m$},$n \leq m$，如果存在数字序列$1 \leq j_1 \leq j_2 \leq ... \leq j_n \leq m$, 满足$a_1 \subseteq b_{j_1}, a_2 \subseteq b_{j_2}...a_n \subseteq b_{j_n} $，则称A是B的子序列。当然反过来说， B就是A的超序列。

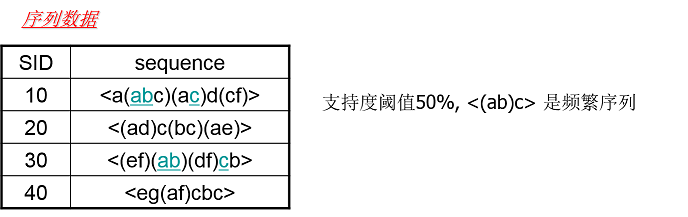
　　　　而频繁序列则和我们的频繁项集很类似，也就是频繁出现的子序列。比如对于下图，支持度阈值定义为50%，也就是需要出现两次的子序列才是频繁序列。而子序列<(ab)c>是频繁序列，因为它是图中的第一条数据和第三条序列数据的子序列，对应的位置用蓝色标示。

3. PrefixSpan算法的一些概念

　　　　PrefixSpan算法的全称是Prefix-Projected Pattern Growth，即前缀投影的模式挖掘。里面有前缀和投影两个词。那么我们首先看看什么是PrefixSpan算法中的前缀prefix。

　　　　在PrefixSpan算法中的前缀prefix通俗意义讲就是序列数据前面部分的子序列。如果用严格的数学描述，前缀是这样的：对于序列A={$a_1,a_2,...a_n$}和序列B={$b_1,b_2,...b_m$},$n \leq m$，满足$a_1 =b_1 , a_2 = b_2...a_{n-1} = b_{n-1} $,而$a_n \subseteq b_n $，则称A是B的前缀。比如对于序列数据B=<a(abc)(ac)d(cf)>，而A=<a(abc)a>,则B是A的前缀。当然B的前缀不止一个，比如<a>, <aa>, <a(ab)> 也都是B的前缀。

　　　　看了前缀，我们再来看前缀投影，其实前缀投影这儿就是我们的后缀，有前缀就有后缀嘛。前缀加上后缀就可以构成一个我们的序列。下面给出前缀和后缀的例子。对于某一个前缀，序列里前缀后面剩下的子序列即为我们的后缀。如果前缀最后的项是项集的一部分，则用一个“_”来占位表示。

　　　　下面这个例子展示了序列<a(abc)(ac)d(cf)>的一些前缀和后缀，还是比较直观的。要注意的是，如果前缀的末尾不是一个完全的项集，则需要加一个占位符。

　　　　在PrefixSpan算法中，相同前缀对应的所有后缀的结合我们称为前缀对应的投影数据库。

4. PrefixSpan算法思想

　　　　现在我们来看看PrefixSpan算法的思想，PrefixSpan算法的目标是挖掘出满足最小支持度的频繁序列。那么怎么去挖掘出所有满足要求的频繁序列呢。回忆Aprior算法，它是从频繁1项集出发，一步步的挖掘2项集，直到最大的K项集。PrefixSpan算法也类似，它从长度为1的前缀开始挖掘序列模式，搜索对应的投影数据库得到长度为1的前缀对应的频繁序列，然后递归的挖掘长度为2的前缀所对应的频繁序列，。。。以此类推，一直递归到不能挖掘到更长的前缀挖掘为止。

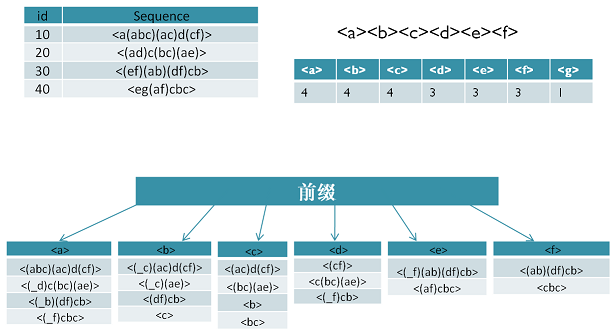
　　　　比如对应于我们第二节的例子，支持度阈值为50%。里面长度为1的前缀包括<a>, <b>, <c>, <d>, <e>, <f>,<g>我们需要对这6个前缀分别递归搜索找各个前缀对应的频繁序列。如下图所示，每个前缀对应的后缀也标出来了。由于g只在序列4出现，支持度计数只有1，因此无法继续挖掘。我们的长度为1的频繁序列为<a>, <b>, <c>, <d>, <e>，<f>。去除所有序列中的g，即第4条记录变成<e(af)cbc>

　　　　
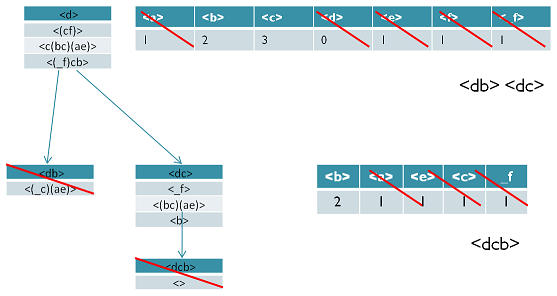
　　　　现在我们开始挖掘频繁序列,分别从长度为1的前缀开始。这里我们以d为例子来递归挖掘，其他的节点递归挖掘方法和Ｄ一样。方法如下图，首先我们对ｄ的后缀进行计数，得到{a:1, b:2, c:3, d:0, e:1, f:1，_f:1}。注意f和_f是不一样的，因为前者是在和前缀d不同的项集，而后者是和前缀d同项集。由于此时a,d,e,f,_f都达不到支持度阈值，因此我们递归得到的前缀为d的2项频繁序列为<db>和<dc>。接着我们分别递归db和dc为前缀所对应的投影序列。首先看db前缀，此时对应的投影后缀只有<_c(ae)>,此时_c,a,e支持度均达不到阈值，因此无法找到以db为前缀的频繁序列。现在我们来递归另外一个前缀dc。以dc为前缀的投影序列为<_f>, <(bc)(ae)>, <b>，此时我们进行支持度计数，结果为{b:2, a:1, c:1, e:1, _f:1}，只有b满足支持度阈值，因此我们得到前缀为dc的三项频繁序列为<dcb>。我们继续递归以<dcb>为前缀的频繁序列。由于前缀<dcb>对应的投影序列<(_c)ae>支持度全部不达标，因此不能产生4项频繁序列。至此以d为前缀的频繁序列挖掘结束，产生的频繁序列为<d><db><dc><dcb>。

　　　　同样的方法可以得到其他以<a>, <b>, <c>, <e>, <f>为前缀的频繁序列。

5. PrefixSpan算法流程

　　　　下面我们对PrefixSpan算法的流程做一个归纳总结。

　　　　输入：序列数据集S和支持度阈值$\alpha$

　　　　输出：所有满足支持度要求的频繁序列集

　　　　1）找出所有长度为1的前缀和对应的投影数据库

　　　　2）对长度为1的前缀进行计数，将支持度低于阈值$\alpha$的前缀对应的项从数据集S删除，同时得到所有的频繁1项序列，i=1.

　　　　3）对于每个长度为i满足支持度要求的前缀进行递归挖掘：

　　　　　　a) 找出前缀所对应的投影数据库。如果投影数据库为空，则递归返回。

　　　　　　b) 统计对应投影数据库中各项的支持度计数。如果所有项的支持度计数都低于阈值$\alpha$，则递归返回。

　　　　　　c) 将满足支持度计数的各个单项和当前的前缀进行合并，得到若干新的前缀。

　　　　　　d) 令i=i+1，前缀为合并单项后的各个前缀，分别递归执行第3步。

6. PrefixSpan算法小结

　　　　PrefixSpan算法由于不用产生候选序列，且投影数据库缩小的很快，内存消耗比较稳定，作频繁序列模式挖掘的时候效果很高。比起其他的序列挖掘算法比如GSP,FreeSpan有较大优势，因此是在生产环境常用的算法。

　　　　PrefixSpan运行时最大的消耗在递归的构造投影数据库。如果序列数据集较大，项数种类较多时，算法运行速度会有明显下降。因此有一些PrefixSpan的改进版算法都是在优化构造投影数据库这一块。比如使用伪投影计数。

　　　　当然使用大数据平台的分布式计算能力也是加快PrefixSpan运行速度一个好办法。比如Spark的MLlib就内置了PrefixSpan算法。

　　　　不过scikit-learn始终不太重视关联算法，一直都不包括这一块的算法集成，这就有点落伍了。

（欢迎转载，转载请注明出处。欢迎沟通交流： pinard.liu@ericsson.com）