HDU 4472 Count（数学 递归）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4472

Problem Description

Prof. Tigris is the head of an archaeological team who is currently in charge of an excavation in a site of ancient relics.

This site contains relics of a village where civilization once flourished. One night, examining a writing record, you find some text meaningful to you. It reads as follows.

“Our village is of glory and harmony. Our relationships are constructed in such a way that everyone except the village headman has exactly one direct boss and nobody will be the boss of himself, the boss of boss of himself, etc. Everyone expect the headman
is considered as his boss’s subordinate. We call it relationship configuration. The village headman is at level 0, his subordinates are at level 1, and his subordinates’ subordinates are at level 2, etc. Our relationship configuration is harmonious because
all people at same level have the same number of subordinates. Therefore our relationship is …”

The record ends here. Prof. Tigris now wonder how many different harmonious relationship configurations can exist. He only cares about the holistic shape of configuration, so two configurations are considered identical if and only if there’s a bijection of
n people that transforms one configuration into another one.

Please see the illustrations below for explanation when n = 2 and n = 4.




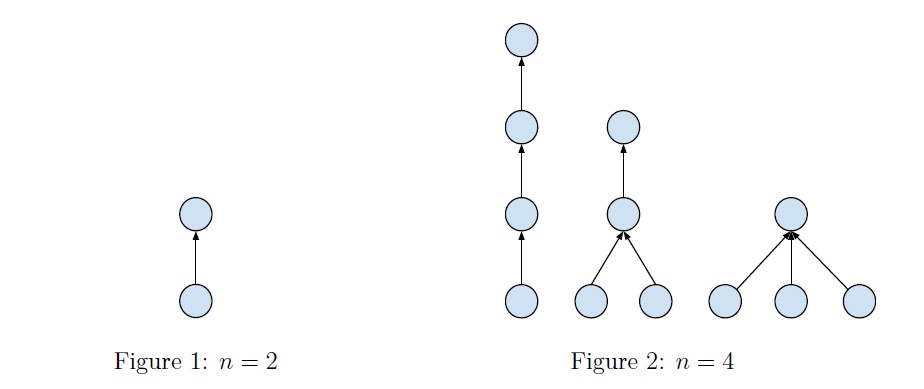
The result might be very large, so you should take module operation with modules 10⁹ +7 before print your answer.

 

Input

There are several test cases.

For each test case there is a single line containing only one integer n (1 ≤ n ≤ 1000).

Input is terminated by EOF.

 

Output

For each test case, output one line “Case X: Y” where X is the test case number (starting from 1) and Y is the desired answer.

 

Sample Input

1
2
3
40
50
600
700

 

Sample Output

Case 1: 1
Case 2: 1
Case 3: 2
Case 4: 924
Case 5: 1998
Case 6: 315478277
Case 7: 825219749

 

Source

2012 Asia Chengdu Regional Contest

题意：

有n个点，使之构成一个树。要求每一层的每一个节点的子节点数要同样。问有多少中构造法！

PS:

对于n个点，先将第一个节点（父节点）去掉。由于父节点仅仅有一个，还剩下
n-1 个点，

由于每一层的每一个节点的子节点数要同样，所以将这
n-1 个节点m等分，每份为（n-1)/m个点，

再递归求解就可以。

代码例如以下：

#include <cstdio>
#include <cstring>
#define mod 1000000007
int dp[1017];
void init()
{
    dp[1] = 1;
    dp[2] = 1;
    dp[3] = 2;
    for(int i = 4; i <= 1000; i++)
    {
        for(int j = 1; j < i; j++)
        {
            if((i-1)%j == 0)
            {
                dp[i]+=dp[(i-1)/j];
                dp[i] %= mod;
            }
        }
    }
}
int main()
{
    int n;
    int cas = 0;
    init();
    while(~scanf("%d",&n))
    {
        printf("Case %d: %d\n",++cas,dp[n]);
    }
    return 0;
}