T 分布（近似标准正态分布）

1.1      定义

定义：假设X服从标准正态分布N（0,1），Y服从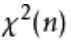卡方分布，那么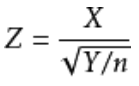的分布称为自由度为n的t分布,记为。

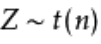T分布密度函数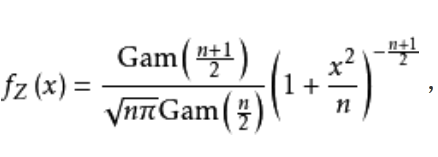其中，Gam(x)为伽马函数。

可用于两组独立计量资料的假设检验。

由于在实际工作中，往往σ（总体方差）是未知的，常用s（样本方差）作为σ总体方差的估计值，为了与u变换（正态化变换）区别，称为t变换，统计量t 值的分布称为t分布。【u分布也叫标准正态分布】

u变换：[(X-μ)/σ]转化成标准正态变量u，以使原来各种形态的正态分布都转换为μ=0，σ=1的标准正态分布（standard normaldistribution），亦称u分布。

在概率论和统计学中，t-分布（t-distribution）用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知（例如在样本数量足够多时），则应该用正态分布来估计总体均值。

经常应用在对呈正态分布的总体的均值进行估计。它是对两个样本均值差异进行显著性测试的学生t测定的基础。t检定改进了Z检定（en:Z-test），不论样本数量大或小皆可应用。在样本数量大（超过120等）时，可以应用Z检定，但Z检定用在小的样本会产生很大的误差，因此样本很小的情况下得改用学生t检定。

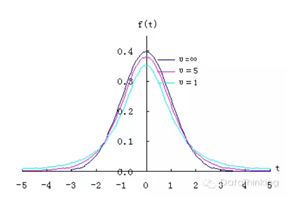
t分布曲线形态与n（确切地说与自由度df）大小有关。与标准正态分布曲线相比，自由度df越小，t分布曲线愈平坦，曲线中间愈低，曲线双侧尾部翘得愈高；自由度df愈大，t分布曲线愈接近正态分布曲线，当自由度df=∞时，t分布曲线为标准正态分布曲线。

当总体的标准差是未知的但却又需要估计时，我们可以运用t-分布。

【特征】：

（1）以0为中心，左右对称的单峰分布；

（2）其数学期望E(Z) = 0，n>1;方差D(Z)=n/n-2 , n>2 。

（3）t分布是一簇曲线，其形态变化与n（确切地说与自由度df）大小有关。自由度df越小，t分布曲线越低平；自由度df越大，t分布曲线越接近标准正态分布（u分布）曲线；

（4）随着自由度逐渐增大，t分布逐渐接近标准正态分布。

【本质】：

T分布本质上和标准正态分布没有太大本质差别，可以说就是标准正态分布的一个近似分布。而标准正态分布只是正态分布的一个特殊情况。综上，从本质上说，T分布就是正态分布的一种特殊的近似。

t分布是正态分布的小样本形态。

①正态分布是与自由度无关的一条曲线； t分布是依自由度而变的一组曲线。

② t分布较正态分布顶部略低而尾部稍高。