Usaco 2019 Jan Platinum

Usaco 2019 Jan Platinum

　　要不是昨天老师给我们考了这套题，我都不知道usaco还有铂金这么一级。

　　插播一则新闻：杨神坚持认为铂金比黄金简单，原因竟是：铜 汞 银 铂 金（金属活动性顺序表）

　　Usaco真是慢的不行，所以就贴洛谷链接啦。

　　

　　Redistricting: https://www.luogu.org/problemnew/show/P5202

　　题意概述：给出一个长度为N的序列，由'H'和'G'组成，将它分为任意段，每段的长度不超过 $K$ ,要求最小化(H比较少的段)的数量。$k<=n<=3 \times 10^5$

　　首先可以将原序列中的G视为一，做一遍前缀和，那么就有了一个 $O(NK)$ 的朴素dp:

　　$dp_i=min \{dp_j+[(s_i-s_j) \times 2 <=(i-j)]\space |\space i-j<=k \}$

　　还需要一些优化，首先发现里面那个式子可以拆开，定义一个新的数组 $g_i=i-2 \times s_i$，这样只要满足 $g_i>g_j$ 就可以无代价转移，否则代价为一。所以一开始想到的是用权值线段树维护，但这样删除的时候可能会有一点麻烦，所以在线段树的叶子节点还得用单调队列维护，感觉写不动就弃了。后来又想到可以用平衡树来做，但是好像删除也有点问题，所以也弃了。这时我突然发现这道题很特殊，代价最多为1，所以可以用一个简单的单调队列来做。

　　要用单调队列首先得明确一点，就是按照哪一维来弹出点。如果按照 $g$ 数组来做...很显然是不可以的。但是按照 $dp$ 数组来做，相同时再按照 $g$ 就是正确的了。解释一下原因吧：假设有两个决策点 $a$ $b$，如果 $dp[a]<dp[b]$，那么无论如何都可以从 $a$ 转移，因为 $dp$ 值都是整数，那么两个不相等的数之间至少差一，所以从 $a$ 转移不会比从 $b$ 转移更差；如果两个决策点的 $dp$ 值相等，则优先选择那个比较难产生代价的决策，正确性显然。复杂度 $O(N)$ 官方题解给的是 $O(NlogN)$ 的做法，在我的电脑上不开 $O_2$ 会 $T$,所以就不搬过来了。

　　

# include <cstdio>
# include <iostream>
# include <cstring>
# define nl (n<<)
# define nr (n<<|)
# define R register int

using namespace std;

const int maxn=;
const int inf=;
int n,k,a[maxn],f[maxn],g[maxn],q[maxn],H=,T;
char s[maxn];

void add (int x)
{
    while(H<=T&&((f[x]<f[ q[T] ])||(f[x]==f[ q[T] ]&&g[x]<=g[ q[T] ]))) T--;
    q[++T]=x;
}

void del (int x) { while (H<=T&&q[H]<=x) H++; }

int ask (int x)
{
    if(g[ q[H] ]<g[x]) return f[ q[H] ];
    return f[ q[H] ]+;
}

int main()
{
    scanf("%d%d",&n,&k);
    scanf("%s",s+);
    for (R i=;i<=n;++i)
    {
        if(s[i]=='G') a[i]=a[i-]+;
        else a[i]=a[i-];
        g[i]=i-*a[i];
    }
    f[]=;
    for (R i=;i<=n;++i)
    {
        add(i-);
        if(i-k->=)
            del(i-k-);
        f[i]=ask(i);
    }
    printf("%d",f[n]);
    return ;
}

My Code

　　exercise：https://www.luogu.org/problemnew/show/P5203

　　题意概述：首先给出一棵树，再给出一些连接树上两点的边，求有多少个环恰好经过两条非树边。$n,m<=10^5$

　　考试的时候打了暴力，结果只有样例分...网上关于这场比赛的中文题解好像很少，所以我就翻译一下官方题解好了(有的地方会省掉一些话，但是意思应该是不变的.)： And,官方题解为什么每句话都要加个"我们"?

　　首先想一想哪些 "非树边" 对可以构成合法答案。我们定义一条非树边的 "路径" 为它连接的两点在树上的路径。如果两条非树边的 "路径" 有边相交（有一样的边），那么这就是一组合法的答案。

　　现在我们有了一个新的问题：如何判断有边相交的树上路径对数？首先我们认为这棵树是任意生根的(这句话只是为了翻出来好玩，其实意思就是无根树)。一条路径可能会有拐点，所以统计起来比较麻烦。那么将它拆成两条路径，一条是从A到LCA的，一条是从LCA到B的，再统计相交的路径会不会好做一点呢？如果用这种统计法，可能会有的路径对被重复计算，然而，重复计算的答案可以很容易地算出来。当且仅当两条路径的LCA相同，而且端点连接到LCA的方式相同（对应端点属于LCA的同一棵子树）时，这个答案才会被统计两次，所以我们可以先计算出这样路径对的数量，最后再从答案中减去即可。这样以来，我们就可以忽视重复计算的影响，转而解决一种非常简单的路径问题。

　　我们的问题现在被简化了。我们有一些从某个节点到它的某个祖先的路径，而且我们希望求出边相交的路径对数。考虑一个类似但更简单的问题：给出一些开区间（A,B），求有多少个区间相交？对于每个区间分别求出起点在它的范围内的区间数目，加起来就是答案（注意，如果两个区间具有相同的端点，答案可能会少一，所以要特殊处理），对于树上的路径，其实也没有什么差别，预处理一遍，做一个树上差分就可以了。当然，还是要注意有相同端点的那些路径。

　　题解程序的实现中有一些小trick，就是对于每条路径，认为它的起点是路径上深度次小的那个点，这样就巧妙的避免了，两条路径仅在端点处重合的问题。

　　

 # include <cstdio>
 # include <iostream>
 # include <map>
 # define R register int
 # define ll long long

 using namespace std;

 const int maxn=;
 int firs[maxn],h=,n,m,x[maxn],y[maxn],l[maxn],a,b,dep[maxn],f[maxn][];
 struct edge { int too,nex; }g[maxn<<];
 map <ll,int> M;
 ll ans,d[maxn];

 int read()
 {
     R x=;
     char c=getchar();
     while (!isdigit(c)) c=getchar();
     while (isdigit(c)) x=(x<<)+(x<<)+(c^),c=getchar();
     return x;
 }

 void dfs (int x)
 {
     int j;
     for (R i=firs[x];i;i=g[i].nex)
     {
         j=g[i].too;
         if(dep[j]) continue;
         f[j][]=x;
         for (R k=;k<=;++k) f[j][k]=f[ f[j][k-] ][k-];
         dep[j]=dep[x]+;
         dfs(j);
     }
 }

 int lca (int x,int y)
 {
     if(dep[x]>dep[y]) swap(x,y);
     for (R i=;i>=;--i) if(dep[y]-(<<i)>=dep[x]) y=f[y][i];
     if(x==y) return x;
     for (R i=;i>=;--i) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
     return f[x][];
 }

 int lcas (int x,int y)
 {
     if(x==y) return -;
     for (R i=;i>=;--i) if(dep[x]-(<<i)>dep[y]) x=f[x][i];
     return x;
 }

 void pushdown (int x)
 {
     int j;
     for (R i=firs[x];i;i=g[i].nex)
     {
         j=g[i].too;
         if(dep[j]<dep[x]) continue;
         d[j]+=d[x];
         pushdown(j);
     }
 }

 void add (int x,int y)
 {
     g[++h].nex=firs[x];
     g[h].too=y;
     firs[x]=h;
 }

 int main()
 {
     n=read(),m=read();
     m-=(n-);
     for (R i=;i<n;++i)
     {
         a=read(),b=read();
         add(a,b),add(b,a);
     }
     dep[]=;
     dfs();
     for (R i=;i<=m;++i)
     {
         x[i]=read(),y[i]=read();
         l[i]=lca(x[i],y[i]);
         a=lcas(x[i],l[i]);
         b=lcas(y[i],l[i]);
         if(a>b) swap(a,b);
         if(a!=-) d[a]++,ans-=d[a];
         if(b!=-) d[b]++,ans-=d[b];
         if(a!=-&&b!=-)
         {
             ans-=M[ a*n+b ];
             M[ a*n+b ]++;
         }
     }
     pushdown();
     for (R i=;i<=m;++i)
         ans+=d[ x[i] ]+d[ y[i] ]-*d[ l[i] ];
     printf("%lld",ans);
     return ;
 }

My Code

　　tracking2:https://www.luogu.org/problemnew/show/P5204

　　题意概述：给出对于长度为n的序列，窗口大小为k的滑动窗口最小值，求有多少原序列满足要求.额外要求:原序列中的数不能大于1e9.$k<=n<=10^5$

　　这题好毒瘤...考场写了一个假装 $k<=10$ 的状压dp，只有样例分。那么下面是翻译的英文题解。(这次写题解的人稍微少用了一些“我们”)：

　　首先，介绍一种记数法。给出一个序列 $a_1, a_2, \ldots a_n$ (小$n$,而不是整个序列的长度$N$), 也就是滑动窗口的最小值：

　　$\{\min(a_1, a_2, \ldots , a_K), \min(a_2, a_3, \ldots , a_{K+1}), \ldots \min(a_{n - K + 1}, a_{n - K + 2}, \ldots , a_n) \}$

　　当看到一个接近这样的问题时，想想它的简化版本往往是很有帮助的。我们现在来看这样一个问题：有多少序列的滑动窗口最小值是这样的？

　　$\underbrace{v, v, \ldots, v}_{N - K + 1 \text{ times }}?$

​ 　　定义 $MX = 10^9$ , $x=MX−v$ . 定义 $dp[u]$ 为长度为 $u$ 的序列满足滑动窗口最小值全是 $v$，而且以 $v$ 结尾。下面通过枚举最右端的那个 $v$ 来计算答案，我们就得到了如下方程：

　　$DP[v] = DP[v-1] + xDP[v-2] + \ldots + x^{K - 1}DP[v - K]$

　　在这里 $x$ 表示严格大于 $v$ 的数的数目.这样就有了一个复杂度为 $O(NK)$ 的解法, 不过我们还可以做得更好，像这样:

　　$DP[v+1] = DP[v] + x(DP[v] - x^{K - 1}DP[v - K])$

　　这样就是 $O(N)$ 了。定义 $c(len,v)$ 为长度为 $len$ ,滑动窗口最小值全为 $v$ 且以 $v$ 结尾的序列个数.

　　现在我们已经解决了这个简单的问题。再从整体上看一看原来的这个问题。假设滑动窗口中两个相邻的数不相同，而且不失一般性地假设左边比右边大，也就是说：

　　$a = \min(a_i, a_{i + 1}, \ldots , a_{i + K - 1}) > \min(a_{i+1}, a_{i+2}, \ldots , a_{i + K}) = b$

　　因为 $a = \min(a_i, a_{i + 1}, \ldots , a_{i + K - 1}) \le \min(a_{i + 1}, a_{i + 2}, \ldots , a_{i + K - 1})$ 所以说 $a_{i+K}=b$ .

　　这就表明，如果两个滑动窗口的值是不同的，我们就可以直接知道某些值。这样就引出了一种新的表示法：将滑动窗口表示为一些数对 (值，连续出现次数)，举个例子：

　　$(5, 3, 3, 3, 3, 2) \mapsto ((5, 1), (3, 4), (2, 1))$.

　　下一步可能最好还是结合一个例子来解释。假设 $K=2$, 滑动窗口的值为 $(2,2,2,3,3,3,1,1)$ . 根据刚刚的推断，序列就可以被表示为这样的形式：$(a,b,2,c,d,e,f,1,g)$ . 现在 $c,d,e,f$ 的滑动窗口最小值就是(3,3,3), $a,b$ 的滑动窗口最小值就是(2,2), $g$的滑动窗口最小值就是(1)。因此问题就可以转化为最早的那个形式，相当于求$c(3,4)×c(2,2)×c(1,1)$.

　　还有两个小问题：一个是结尾，一个是...这句我真的翻译不出来了，直接粘过来：“ranges which are surrounded by two larger ranges are a bit subtle”；

　　最后是我自己的理解了：如果不合并，有的段就会被算多次，但是采用一些巧妙的方法，不压缩应该也是可以的。

　　我翻的很像机翻吗？其实我写的中文题解有时候看起来也像机翻。

　　

 # include <cstdio>
 # include <cstring>
 # include <iostream>
 # define R register int
 # define ll long long
 using namespace std;

 const int maxn=;
 const ll mod=;
 const int mx=;
 int dp[maxn],a[maxn],n,k;
 int sub (int a,int b) { a-=b; a=(a%mod+mod)%mod; return a; }
 int mul (int a,int b) { a=1LL*a*b%mod; return a; }

 int qui (int a,int b)
 {
     int s=;
     while(b)
     {
         if(b&) s=mul(s,a)%mod;
         a=mul(a,a)%mod;
         b>>=;
     }
     return s;
 }

 int c (int v,int len)
 {
     dp[]=dp[]=;
     int x=mx-v;
     int p=qui(x,k);
     for (R i=;i<=len;++i)
     {
         dp[i]=mul(x+,dp[i-]);
         if(i-k-<) continue;
         dp[i]=sub(dp[i],mul(p,dp[i-k-]));
     }
     return dp[len];
 }

 int main()
 {
     scanf("%d%d",&n,&k);
     for (R i=;i<=n-k+;++i)
         scanf("%d",&a[i]);
     int l=,r,ans=,len;
     while(l<=n-k+)
     {
         r=l;
         while(a[r+]==a[l]) r++;
         len=r-l+k;
         if(l!=&&a[l-]>a[l]) len-=k;
         if(r!=n-k+&&a[r+]>a[r]) len-=k;
         if(len>=) ans=mul(ans,c(a[l],len+));
         l=r+;
     }
     printf("%d",ans);
     return ;
 }

My Code

　　求解C那里，我给len加了一个一，这是为什么呢...因为刚刚的定义是：$c(len,v)$ 为长度为 $len$ ,滑动窗口最小值全为 $v$ 且以 $v$ 结尾的序列个数，但是实际应用中，最后一个数并不需要是 $v$，所以多算一位，再把最后一位截去即可。

　　终于全都补完了！这套题的实现难度不是很大，但是思路却很巧妙。

　　老师也发了一份题解，但是那个做法看起来比较难写，可能大概好懂一点？反正我没懂。一并放上来，如果有人能看懂也是件好事。相同段的处理是一样的，但是套一层rmq我就不懂是什么操作了。

　　

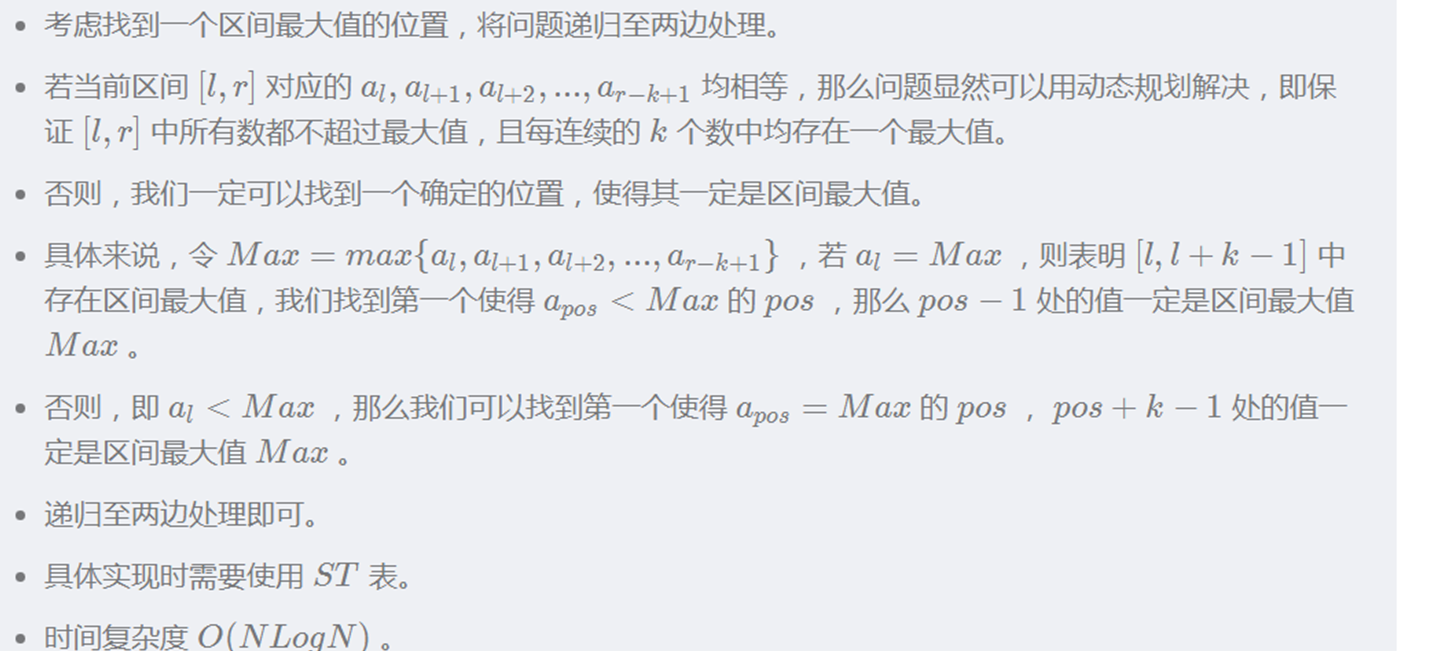
　　那么下一场再见啦！虽然我大概率不打下一场

---shzr